📌

如果你喜歡我寫的文章，可以把我的公眾號設為星標 🌟，這樣每次有更新就可以及時推送給你啦。

前面兩天畫了點和線，今天我們來畫一個最簡單也是最強大的面——三角形。

本文主要講解三角形繪製演算法的推導和思路（只涉及到一點點的向量知識），最後會給出程式碼實現，大家放心的看下去就好。

📌

本文源碼 👉：toyRenderer-day3-draw-triangle

1.如何畫一個三角形？

在正式開始這一小節前，我們先想一下如何利用上一節的畫線演算法繪製一個實心的三角形。

假設現在平面內有三個不共線的點組成一個三角形，我們可以利用上一節的直線演算法輕易的連接三角形的三條邊，這時候我們會生成一個空心的、封閉的三角形。

那麼這時候問題就轉換為，如何把這個空心的三角形變為一個實心的三角形？

我想大家這時候已經有思路了，就是一行一行地掃描像素，把兩個邊界點之間的像素全部塗滿上色就可以了。

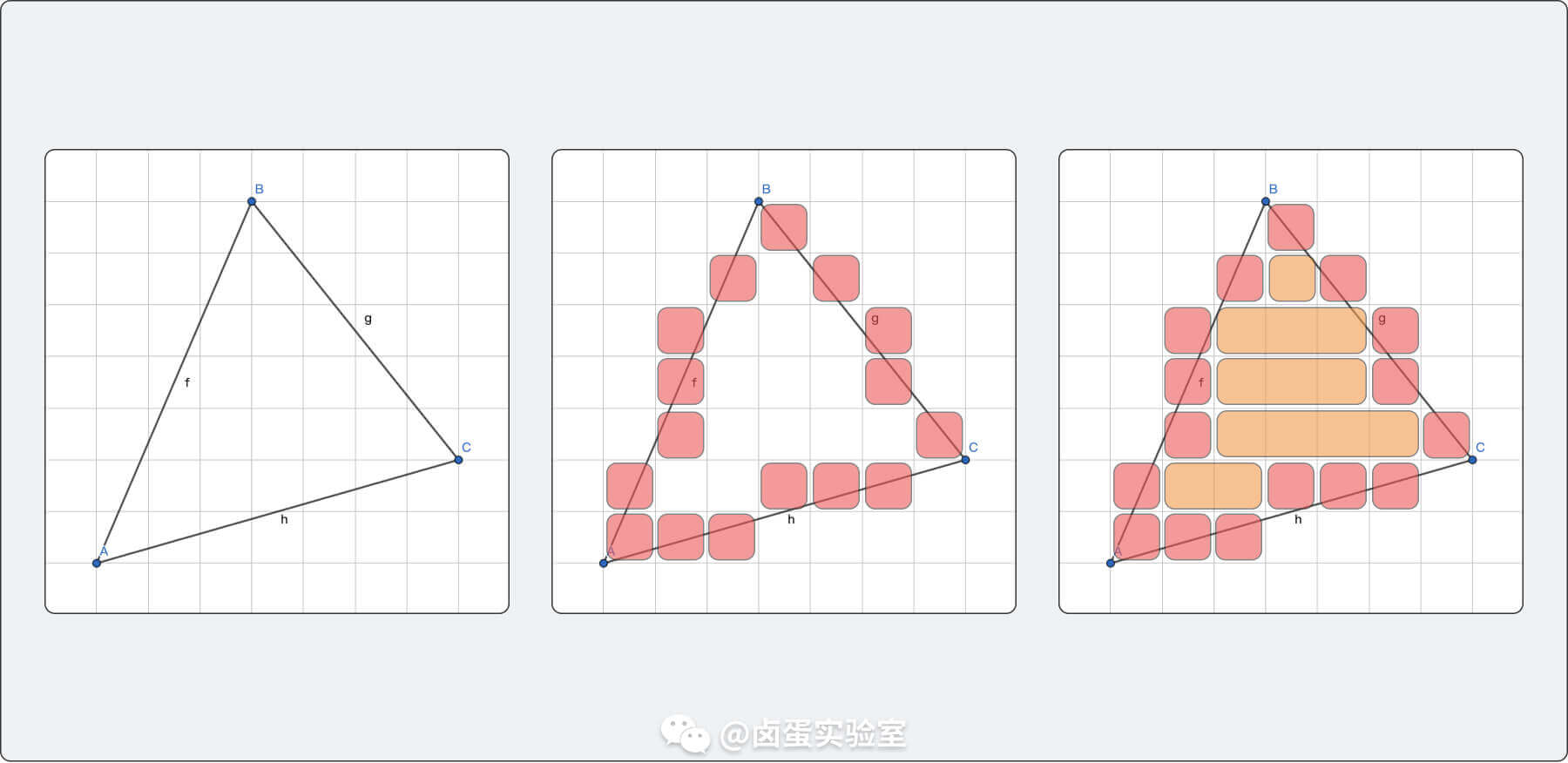
這個方法肯定是可以的，但是實現不是很優雅，也不是業內的主流實現方式。因為基於行掃描的演算法不是本文的重點，所以詳細的推導和程式碼實現就不提供了，感興趣的同學可以自己嘗試實現一下。

2.利用向量叉乘畫三角形

開始本節前先簡單複習一下向量叉乘的幾何意義。

2.1 數學推導

在三維空間中，兩個三維向量 和 做叉乘，會得到一個和已知兩個向量垂直的新向量 。

既然叉乘產生的是一個新向量，那麼它肯定有個方向，我們一般用右手定則來判斷：將右手食指指向 的方向、中指指向 的方向，則此時拇指的方向即為 的方向。

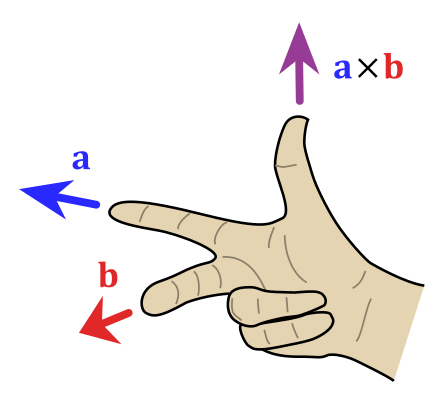
綜上所述，我們可以對向量叉乘做一個嚴謹的定義：

其中 表示 和 在它們所定義的平面上的夾角（）。 和 是向量 和 的模長，而 則是一個與 、 所構成的平面垂直的單位向量，方向由右手定則決定。

有上面的理論，我們就可以判斷兩個向量的相對位置：

• 向量叉乘 向量，如果值為正，則表示 向量在 向量左側
• 向量叉乘 向量，如果值為負，則表示 向量在 向量右側
• 向量叉乘 向量，如果值為零，則表示 向量與 向量共線

會判斷兩條線的相對位置了，我們可以做個理論遷移，利用向量叉乘判斷點和三角形的位置關係。

例如下面這裡例子，對於三角形 來說，把三條邊看作 、 、 三條首尾相連的向量，平面內有一個點 ，我們通過向量叉乘來判斷相對位置：

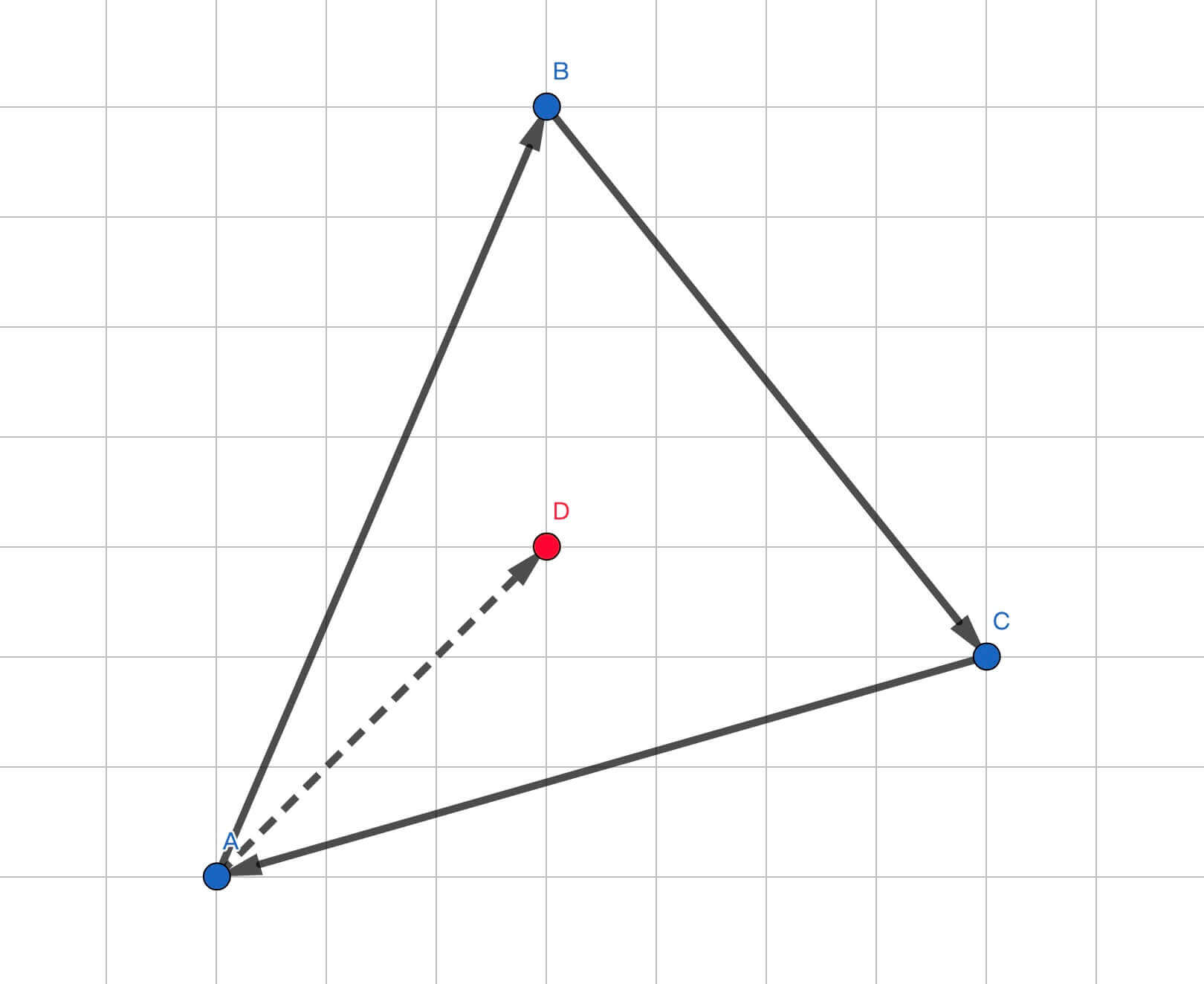
• ，值為正，故 在 左側
• ，值為正，故 在 左側
• ，值為正，故 在 左側

綜合以上三個限制條件，我們可以判斷 在 內。

如果上面三個計算中有值為負的情況，說明 在三角形外；如果有值為 0 的情況，說明 在三角形的邊或頂點上。

2.2 程式碼實現

理論基礎複習完了，我們就可以寫程式碼了。程式碼實現相當簡單，我們構建一個函數 crossProduct，傳入三角形的三個頂點和平面上的任意一點 ，然後根據四個頂點構建出向量計算叉乘就可以了：

// 利用叉乘判斷是否在三角形內部
Vec3i crossProduct(Vec2i *pts, Vec2i P) {
    // 構建出三角形 ABC 三條邊的向量
    Vec2i AB(pts[1].x - pts[0].x, pts[1].y - pts[0].y);
    Vec2i BC(pts[2].x - pts[1].x, pts[2].y - pts[1].y);
    Vec2i CA(pts[0].x - pts[2].x, pts[0].y - pts[2].y);
    
    // 三角形三個頂點和 P 鏈接形成的向量
    Vec2i AP(P.x - pts[0].x, P.y - pts[0].y);
    Vec2i BP(P.x - pts[1].x, P.y - pts[1].y);
    Vec2i CP(P.x - pts[2].x, P.y - pts[2].y);
    
    return Vec3i(AB^AP, BC^BP, CA^CP);
}

程式碼非常的簡單，我們跑一個簡單的例子驗證一下：

void drawSingleTriangle() {
    // 圖片的寬高
    int width  = 200;
    int height = 200;

    TGAImage frame(width, height, TGAImage::RGB);
    Vec2i pts[3] = {Vec2i(10, 10), Vec2i(150, 30), Vec2i(70, 160)};

    Vec2i P;
    // 遍歷圖片中的所有像素
    for (P.x = 0; P.x <= width - 1; P.x++) {
        for (P.y = 0; P.y <= height - 1; P.y++) {
            Vec3i bc_screen  = crossProduct(pts, P);

            // bc_screen 某個分量小於 0 則表示此點在三角形外（認為邊也是三角形的一部分）
            if (bc_screen.x<0 || bc_screen.y<0 || bc_screen.z<0) {
                continue;
            }
            
            image.set(P.x, P.y, color);
        }
    }
    
    frame.flip_vertically();
    frame.write_tga_file("output/day03_cross_product_triangle.tga");
}

看輸出影像，我們已經成功繪製了一個三角形：

📌

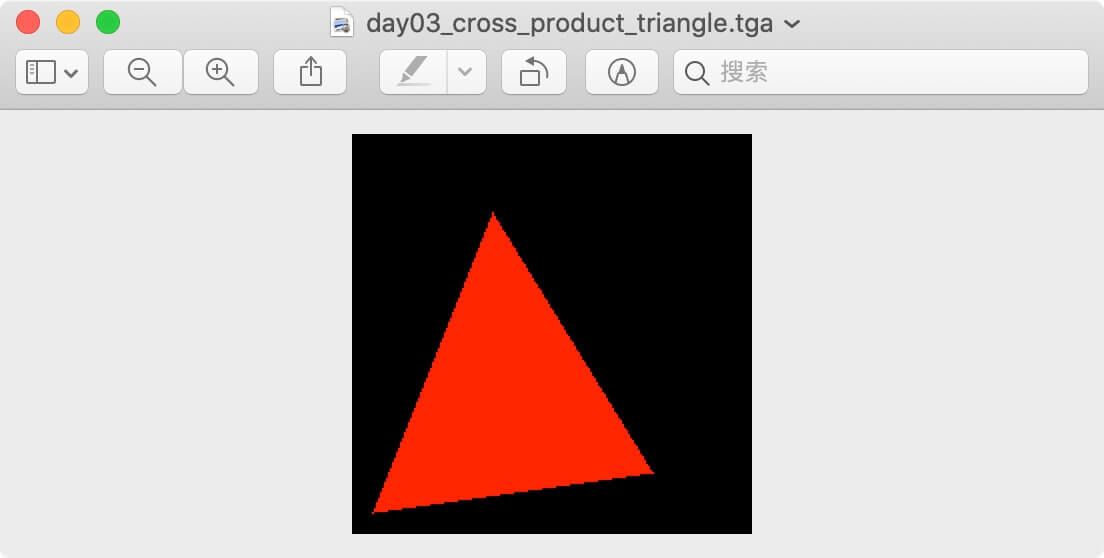
觸不及防的安利：大家可以看我頭像關注🛰️號「滷蛋實驗室」，後台回復「圖形學」獲取經典教材《虎書4》和《Real Time Rendering 4》

3.利用三角形重心坐標畫三角形

本小節介紹一個更通用的定理——重心坐標（Barycentric Coordinate）。其實重心坐標用來畫三角形還是有些大材小用了，他最重要的運用其實是用來做插值，不過插值的具體運用我們後續章節再探討，今天我們看看重心坐標的推導和程式碼實現。

3.1 數學推導

我們暫時只考慮二維平面的三角形。對於一個三角形 來說，假設平面內有一個點 ，很顯然，，， 向量都是線性相關的，也就是說，可以用下式表示 ：

我們把這個三角形放在一個笛卡爾坐標系下，我們就可以這樣表示：

把位置挪一下，合併同類項後， 點的位置可以表示為下式：

結合幾何意義，我們很容易推出：

• 當 、 和 均大於 0 小於 1 時，P 位於三角形內部
• 有一個分量等於 0 時，P 在三角形邊上
• 有兩個變數等於 0 時，P 在某個頂點上

再對第一個式子做一下變形，可以得到下式：

因為三角形位於笛卡爾坐標系內，我們可以把上面的式子沿 和 軸拆分為兩個式子，他們和上式是等價的：

觀察這個式子，我們可以轉換為矩陣乘法的形式：

觀察上面的式子，我們要尋找一個向量 ，它要與向量 和 同時點乘為 0。

稍微思考一下，這不就意味著向量 同時垂直於向量 和 嗎！

所以我們直接求後兩個向量的叉乘就可以求出向量 了。

後兩個向量做叉乘的時候有個小細節需要注意一下，向量叉乘的直接結果（先假設結果為 ）一般只是和 平行，想要正確求出 和 的值，我們需要對向量 除以 ，也就是說 ，，。

這個時候問題就來了，上面的除法成立，必須要建立在 不為 0 的基礎上，那麼我們就要研究一下 為 0 的數學含義了。

根據向量的叉乘公式：

向量可以表示為這樣的行列式：

如果這時候的叉乘結果為 0，把這個行列式從列向量的視角看，就相當於 和 向量叉乘結果為 0，也就是說 和 向量共線。這時候三角形 就退化為一條線段。

對於我們現在應用場景來說，只要檢測到 為 0，就意味著這個三角形退化為一條線段了，我們直接捨棄掉它就好了，對最後的結果也沒有影響。

3.2 程式碼實現

根據上面的公式推導，我們可以直接寫出基於三角形重心坐標的繪製演算法，思路理清了，程式碼實現就非常的簡單：

// 利用重心坐標判斷點是否在三角形內部
Vec3f barycentric(Vec2i *pts, Vec2i P) {
    Vec3i x(pts[1].x - pts[0].x, pts[2].x - pts[0].x, pts[0].x - P.x);
    Vec3i y(pts[1].y - pts[0].y, pts[2].y - pts[0].y, pts[0].y - P.y);
    
    // u 向量和 x y 向量的點積為 0，所以 x y 向量叉乘可以得到 u 向量
    Vec3i u = x^y;
    
    // 由於 A, B, C, P 的坐標都是 int 類型，所以 u.z 必定是 int 類型，取值範圍為 ..., -2, -1, 0, 1, 2, ...
    // 所以 u.z 絕對值小於 1 意味著三角形退化了，直接捨棄
    if(std::abs(u.z) < 1) {
        return Vec3f(-1, 1, 1);
    }
    return Vec3f(1.f- (u.x+u.y) / (float)u.z, u.x / (float)u.z, u.y / (float)u.z);
}

用上面的演算法畫個三角形驗證一下，很完美：

4.繪製模型

演算法寫好了，我們就要投入到實際應用中了，昨天里我們畫了個三維模型的線框圖，今天我們就個這個模型上色。

4.1 隨機著色

為了區分每個三角形，我們隨機給三角形上不同的色：

triangle(screen_coords, frame, TGAColor(rand() % 255, rand() % 255, rand() % 255, 255));

這裡還有個關於性能的小細節。這次我們繪製的影像大小為 800*800，如果按照之前的演算法，每次畫三角形，都要把所有像素遍歷一遍，這個模型大概有 2000 個三角形，那就是要循環 2000*800*800 即 12.8 億 次！

這個量級是很恐怖的，其中很多的運算都是不必要的，比如說下圖，我們其實只要循環由三個頂點計算出的紅色包圍盒裡的像素就可以了，不需要計算圖片內的所有像素：

所以我們要在遍歷像素前加先求一遍三角形包圍盒的邊界，正式畫三角形時只要遍歷包圍盒內的像素就可以了：

// 定義包圍盒
Vec2i boxmin(image.get_width() - 1, image.get_height() - 1);
Vec2i boxmax(0, 0);
// 圖片的邊界
Vec2i clamp(image.get_width() - 1, image.get_height() - 1);

// 查找包圍盒邊界
for (int i = 0; i < 3; i++) {
    // 第一層循環，遍歷三角形的三個頂點
    for (int j = 0; j < 2; j++) {
        // 第二層循環，根據頂點數值縮小包圍盒的範圍
        boxmin.x = std::max(0,        std::min(boxmin.x, pts[i].x));
        boxmin.y = std::max(0,        std::min(boxmin.y, pts[i].y));

        boxmax.x = std::min(clamp.x, std::max(boxmax.x, pts[i].x));
        boxmax.y = std::min(clamp.y, std::max(boxmax.y, pts[i].y));
    }
}

最後我們繪製出的結果就是這樣的，看著還是有些酷炫的：

4.2 簡單的光照著色

隨機著色的好處是可以很清楚的表現出模型各個三角形的輪廓，但是也失去了模型的辨識度，很多細節都丟失了。

我們在這裡引入一個非常簡單的光照模型，認為單位面積上接收到的光，和平面法線與光照方向的餘弦值成正比：

所以著色的思路就很清晰了：

• 我們要先定義一個三維空間里的光照方向（向量），然後計算三維空間里各個三角形的法線（向量）
• 兩個向量歸一化後，然後計算這兩個向量的點乘，會得到一個值
• 這個值小於 0，說明光在三角形的另一側，從物理上看是照射不到三角形表面的，所以直接捨棄此三角形
• 這個值大於 0，值越大，說明單位面積上接收到的光越多，三角形越亮

把上面的思路翻譯成程式碼就是這樣的：

// 這個是用一個模擬光照對三角形進行著色

Vec3f light_dir(0, 0, -1); // 假設光是垂直螢幕的

for (int i = 0; i < model->nfaces(); i++) {
    std::vector<int> face = model->face(i);
    Vec2i screen_coords[3];
    Vec3f world_coords[3];

    // 計算世界坐標和螢幕坐標
    for (int j = 0; j < 3; j++) {
        Vec3f v = model->vert(face[j]);
        // 投影為正交投影，而且只做了個簡單的視口變換
        screen_coords[j] = Vec2i((v.x + 1.) * width / 2., (v.y + 1.) * height / 2.);
        world_coords[j]  = v;
    }

    // 計算世界坐標中某個三角形的法線（法線 = 三角形任意兩條邊做叉乘）
    Vec3f n = (world_coords[2] - world_coords[0]) ^ (world_coords[1] - world_coords[0]);
    n.normalize(); // 對 n 做歸一化處理

    // 三角形法線和光照方向做點乘，點乘值大於 0，說明法線方向和光照方向在同一側
    // 值越大，說明越多的光照射到三角形上，顏色越白
    float intensity = n * light_dir;
    if (intensity > 0) {
        triangle(screen_coords, frame, TGAColor(intensity * 255, intensity * 255, intensity * 255, 255));
    }
}

最後生成的圖片就是這樣的：

到這裡渲染出的影像就有些人樣了，但是大家應該也發現了，上圖的嘴巴和眼睛處看上去怪怪的。這裡的確是有問題，因為它把背後的三角形渲染出來了，要想解決這個問題，就要引入一個新的概念——z-buffer。

推薦直接閱讀原文，更新更及時，閱讀體驗更佳

📌

如果你喜歡我的文章，希望點贊👍 收藏 📁 在看 🌟 三連支援一下！！！謝謝你，這對我真的很重要！

歡迎大家關注我的微信公眾號：滷蛋實驗室，目前專註前端技術，對圖形學也有一些微小研究。

也可以加我的微信 egg_labs，歡迎大家來撩。