Knowledge-Embedded Routing Network for Scene Graph Generation 閱讀筆記
Background
- 論文動機
- 真實世界中關係的分布是非常不平衡的,現存的模型對小頻率的關係表現不好
- 論文貢獻
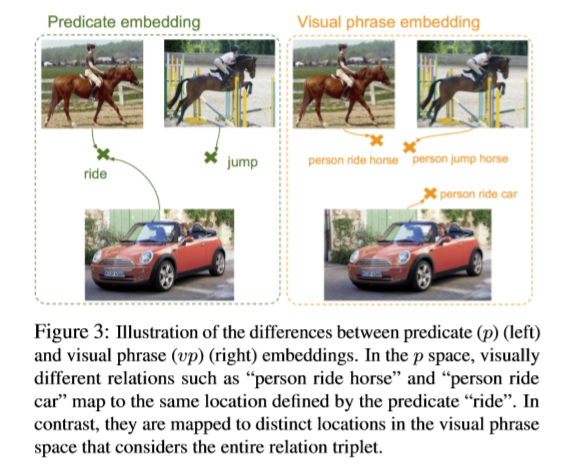
- 作者發現目標對和它們的之間關係的統計相關性能夠有效地調整語義空間,使關係預測不再模糊,很好地解決了關係不平衡分布的問題
- 第一個將顯示地將統計知識用於場景圖生成
Model

primary
場景圖是影像內容的結構化表示。它由類別標籤,每個object的位置和每個object間的關係。這可以被視為三元組集合\mathcal{G}=\{B, O, R\}:
- B=\{b_1,b_2,\cdots,b_n\}為候選區域集合,b_i \in \mathbb{R}^4。
- O = \{o_1,o_2,\cdots,o_n\}為object集合,o_i \in \mathbb{N}。
- R=\left\{r_{1 \rightarrow 2}, r_{1 \rightarrow 3}, \ldots, r_{n \rightarrow n-1}\right\}為關係集合,包括
no-relationship。
對於給定影像I,作者將場景圖概率分布分p(\mathcal{G}|I)解為三個部分:
p(\mathcal{G} \mid I)=p(B \mid I) p(O \mid B, I) p(R \mid O, B, I) (1)
在公式(1)中,p(B \mid I)由Faster RCNN得到。 p(O \mid B, I)根據每個區域對種類標籤進行預測。基於預測的種類標籤,p(R \mid O, B, I)推斷object對之間的關係。
konowledge-embedded routing network
Objetct
object共現的統計資訊是關聯影像中 object 和挑戰object標籤預測的重要線索。因此,作者根據統計關聯性去構建一個圖來關聯影像中的檢測出的區域,並使用圖神經網路在圖上進行消息傳播來,可以學習上下文的表示來預測每個區域的種類標籤。
為此,作者首先計算訓練集中不同種類object統計共現概率。具體地,對於兩個種類c, c^{\prime},作者計算在類別c^{\prime}object存在的情況下,類別c出現的概率m_{cc^{\prime}}。對所有種類對計算弓共現概率,得到矩陣M_{c} \in \mathbb{R}^{C \times C},C為類別數量。
對於給定的兩個區域b_i和b_j,將b_i複製C次,得到節點{b_{i1},b_{i2},\cdots,b_{iC}},b_{ic}表示區域b_i於種類c的相關性。對區域b_j進行相同的操作。直覺地,m_{cc^{\prime}}可以用於關聯節點b_{jc^{\prime}}和b_{ic}。因此,矩陣M_c可用於關聯區域b_i的節點和b_j的節點。最後,關聯所有的區域,並構造圖。
作者使用gated recurrent update mechanism去迭代傳播節點資訊。在時間步t,每個節點b_{ic}的隱藏狀態\mathbf{h}_{ic}^t。由於每個節點對應特定的區域,在時間t=0,作者使用區域的特徵向量去初始化隱藏狀態:
\mathbf{h}_{i c}^{0}=\varphi_{o}\left(\mathbf{f}_{i}\right) (2)
\phi_{o}表是轉換,將\mathbf{f}_i投影到低緯度。在時間步t,每個節點根據圖結構,從它的相鄰節點聚合資訊:
\mathbf{a}_{i c}^{t}=\left[\sum_{j=1, j \neq i}^{n} \sum_{c^{\prime}=1}^{C} m_{c^{\prime} c} \mathbf{h}_{j c^{\prime}}^{t-1}, \sum_{j=1, j \neq i}^{n} \sum_{c^{\prime}=1}^{C} m_{c c^{\prime}} \mathbf{h}_{j c^{\prime}}^{t-1}\right] (3)
然後,模型將\mathcal{a}^t_{ic}和之前的隱藏狀態作為輸入,通過門控機制更新節點的隱藏狀態:
\begin{aligned} \mathbf{z}_{i c}^{t} &=\sigma\left(\mathbf{W}_{o}^{z} \mathbf{a}_{i c}^{t}+\mathbf{U}_{o}^{z} \mathbf{h}_{i c}^{t-1}\right) \\ \mathbf{r}_{i c}^{t} &=\sigma\left(\mathbf{W}_{o}^{r} \mathbf{a}_{i c}^{t}+\mathbf{U}_{o}^{r} \mathbf{h}_{i c}^{t-1}\right) \\ \widetilde{\mathbf{h}}_{i c}^{t} &=\tanh \left(\mathbf{W}_{o} \mathbf{a}_{i c}^{t}+\mathbf{U}_{o}\left(\mathbf{r}_{i c}^{t} \odot \mathbf{h}_{i c}^{t-1}\right)\right) \\ \mathbf{h}_{i c}^{t} &=\left(1-\mathbf{z}_{i c}^{t}\right) \odot \mathbf{h}_{i c}^{t-1}+\mathbf{z}_{i c}^{t} \odot \mathbf{h}_{i c}^{t} \end{aligned} (4)
經過T_0步之後,節點資訊就在整個圖上進行了傳播,同時也得到了每個區域的隱藏狀態\left\{\mathbf{h}_{i 1}^{T_{o}}, \mathbf{h}_{i 2}^{T_{o}}, \ldots, \mathbf{h}_{i C}^{T_{o}}\right\}。然後利用初始的隱藏狀態和最終隱藏狀態計算每個接待你的輸出特徵:
\mathbf{f}_{i c}^{o}=o_{o}\left(\mathbf{h}_{i c}^{0}, \mathbf{h}_{i c}^{T}\right) (5)
o_o表示全連接層,聚合所有關聯的輸出特徵向量,對種類標籤進行預測:
\mathbf{o}_{i}=\phi_{o}\left(\mathbf{f}_{i 1}^{o}, \mathbf{f}_{i 2}^{o}, \ldots, \mathbf{h}_{i C}^{o}\right) (6)
預測的類別標籤為:o_{i}=\operatorname{argmax}\left(\mathbf{o}_{i}\right)
Relationship
對於給定的objetc對類別,它們之間的關係概率分布是高度偏斜的。因此,作者以結構化圖的形式去對object對和關係進行關聯,並用另一種圖神經網路去探索這兩個因素的相互作用,以推斷出object對間的關係。
相似地,計算數據集中統計共現概率來獲得這些相關性。具體來說,對於給定的subject種類c和objetc種類c^{\prime},計算所有關係種類的可能性,並表示為\left\{m_{c c^{\prime} 1}, m_{c c^{\prime} 2}, \ldots, m_{c c^{\prime} K}\right\},K為關係數量。作者使用m_{o_i,o_j,k}表示節點o_i與關係k以及節點o_j與關係k的關聯性。統計共現嵌入圖就被建立了。
模型同樣使用gated recurrent update mechanism去挖掘節點之間的相互作用。對於每個節點v \in V = \{o_i,o_j,1,2\cdots,K\}都在時間t具有隱藏特徵\mathbf{h}_v^t。在時間t=0時,初始化object節點特徵為對應區域的特徵向量,關係節點為object對之間的union區域的特徵向量:
\mathbf{h}_{v}^{0}=\left\{\begin{array}{ll}\varphi_{o^{\prime}}\left(\mathbf{f}_{i}\right) & \text { if } v \text { is the object node } o_{i} \\ \varphi_{r}\left(\mathbf{f}_{i j}\right) & \text { if } v \text { is a relationship node }\end{array}\right. (7)
\phi_{o^{\prime}}和\phi_r為兩個變換,\mathbf{f}_{ij}為編碼了b_j,b_i的聯合區域的特徵向量。在每一個時間步t,關係節點從object節點和關係節點中聚合資訊。
\mathbf{a}_{v}^{t}=\left\{\begin{array}{ll}\sum_{k=1}^{K} m_{o_{i} o_{j} k} \mathbf{h}_{k}^{t-1} & \text { if } v \text { is a object node } \\ m_{o_{i} o_{j} k}\left(\mathbf{h}_{o_{i}}^{t-1}+\mathbf{h}_{o_{j}}^{t-1}\right) & \text { if } v \text { is the relationship node } k\end{array}\right. (8)
相似地,模型結合之前的隱藏狀態\mathbf{h}^{t-1}_{v}與聚合到的資訊a_v^t藉助門控機制更新每個節點的隱藏狀態。重複這樣的操作T_r之後,得到每個節點的最終隱藏狀態\left\{\mathbf{h}_{o i}^{T_{r}}, \mathbf{h}_{o_{j}}^{T_{r}}, \mathbf{h}_{1}^{T_{r}}, \ldots, \mathbf{h}_{K}^{T_{r}},\right\}。然後,使用全連接層節點級別的特徵,並聚合這些特徵去推斷關係:
\begin{aligned} \mathbf{f}_{v}^{o} &=o_{r}\left(\left[\mathbf{h}_{v}^{T_{r}}, \mathbf{h}_{v}^{0}\right]\right) \\ \mathbf{x}_{i \rightarrow j} &=\phi_{r}\left(\left[\mathbf{f}_{o_{i}}^{o}, \mathbf{f}_{o_{j}}^{o}, \mathbf{f}_{1}^{o}, \ldots, \mathbf{f}_{K}^{o}\right]\right) \end{aligned} (9)
\phi_r為關係類別分類器。