李宏毅機器學習課程筆記-5.3神經網路中的反向傳播演算法
鏈式法則(Chain Rule)
- \(z=h(y),y=g(x)\to\frac{dz}{dx}=\frac{dz}{dy}\frac{dy}{dx}\)
- \(z=k(x,y),x=g(s),y=h(s)\to\frac{dz}{ds}=\frac{dz}{dx}\frac{dx}{ds}+\frac{dz}{dy}\frac{dy}{ds}\)
反向傳播演算法(Backpropagation)
變數定義
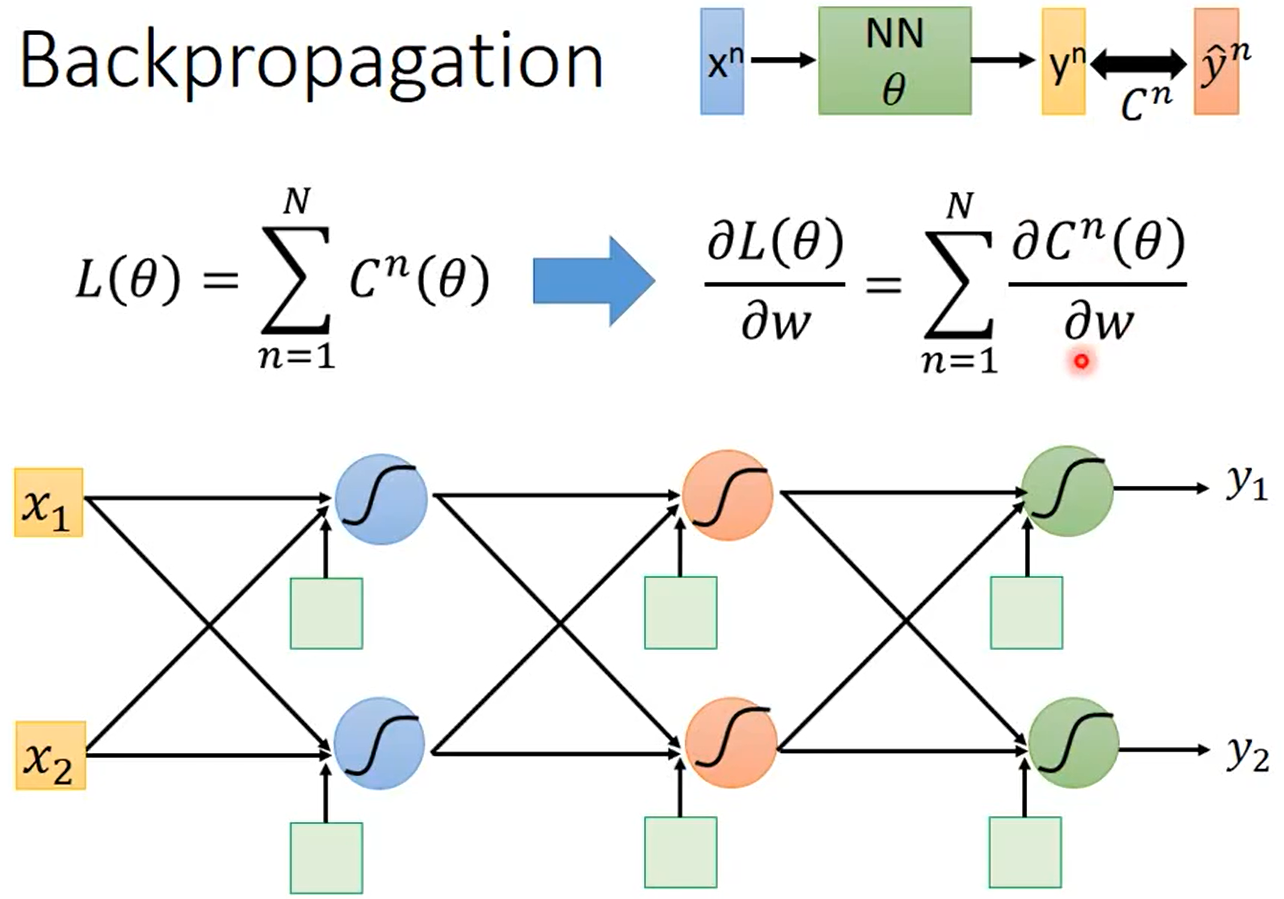
如下圖所示,設神經網路的輸入為\(x^n\),該輸入對應的label是\(\hat y^n\),神經網路的參數是\(\theta\),神經網路的輸出是\(y^n\)。
整個神經網路的Loss為\(L(\theta)=\sum_{n=1}^{N}C^n(\theta)\)。假設\(\theta\)中有一個參數\(w\),那\(\frac{\partial L(\theta)}{\partial w}=\sum^N_{n=1}\frac{\partial C^n(\theta)}{\partial w}\)。
一個神經元的情況
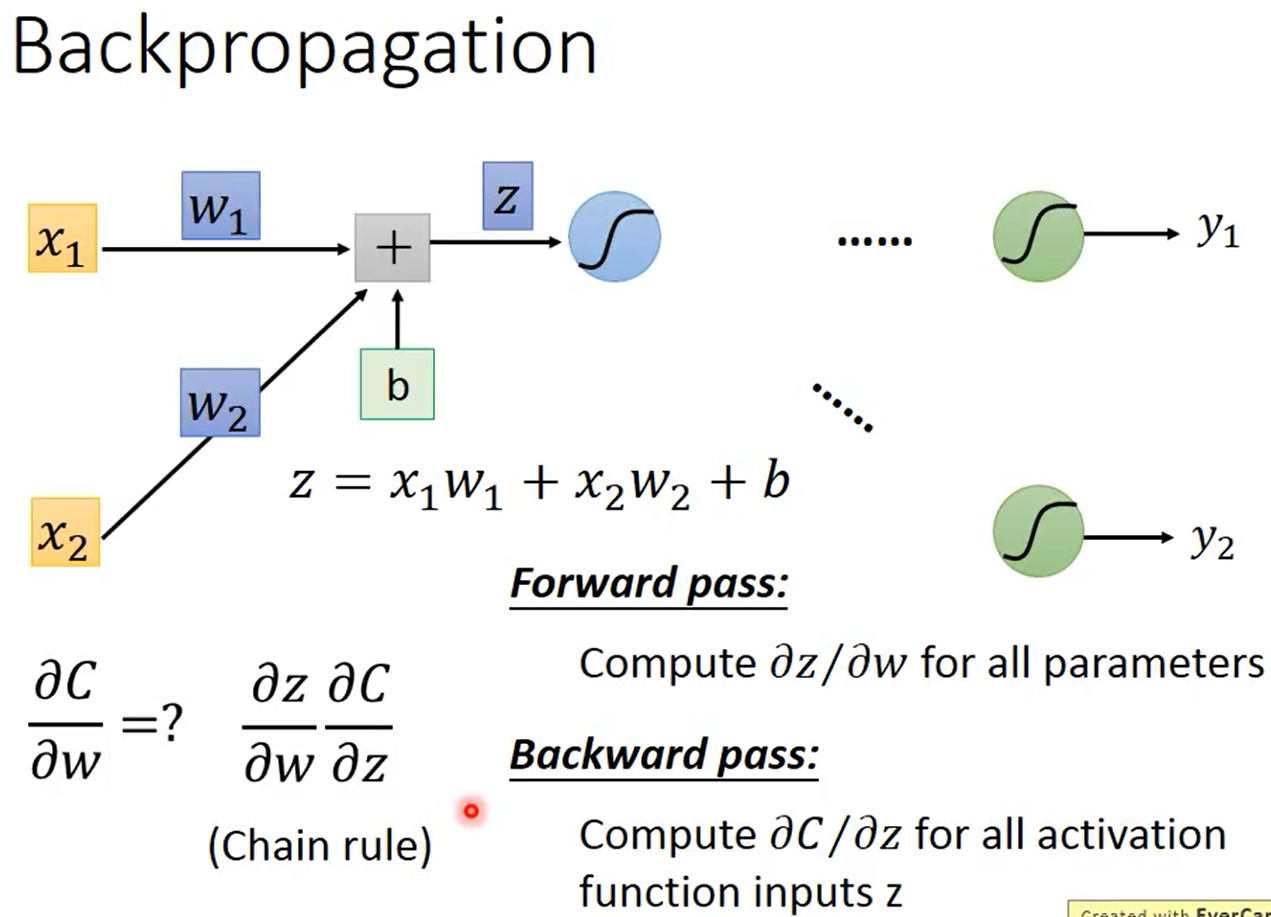
如下圖所示,\(z=x_1w_1+x_2w_x+b\),根據鏈式法則可知\(\frac{\partial C}{\partial w}=\frac{\partial z}{\partial w}\frac{\partial C}{\partial z}\),其中為所有參數\(w\)計算\(\frac{\partial z}{\partial w}\)是Forward Pass、為所有激活函數的輸入\(z\)計算\(\frac{\partial C}{\partial z}\)是Backward Pass。
Forward Pass
Forward Pass是為所有參數\(w\)計算\(\frac{\partial z}{\partial w}\),它的方向是從前往後算的,所以叫Forward Pass。
以一個神經元為例,因為\(z=x_1w_1+x_2w_x+b\),所以\(\frac{\partial z}{\partial w_1}=x_1,\frac{\partial z}{\partial w_2}=x_2\),如下圖所示。
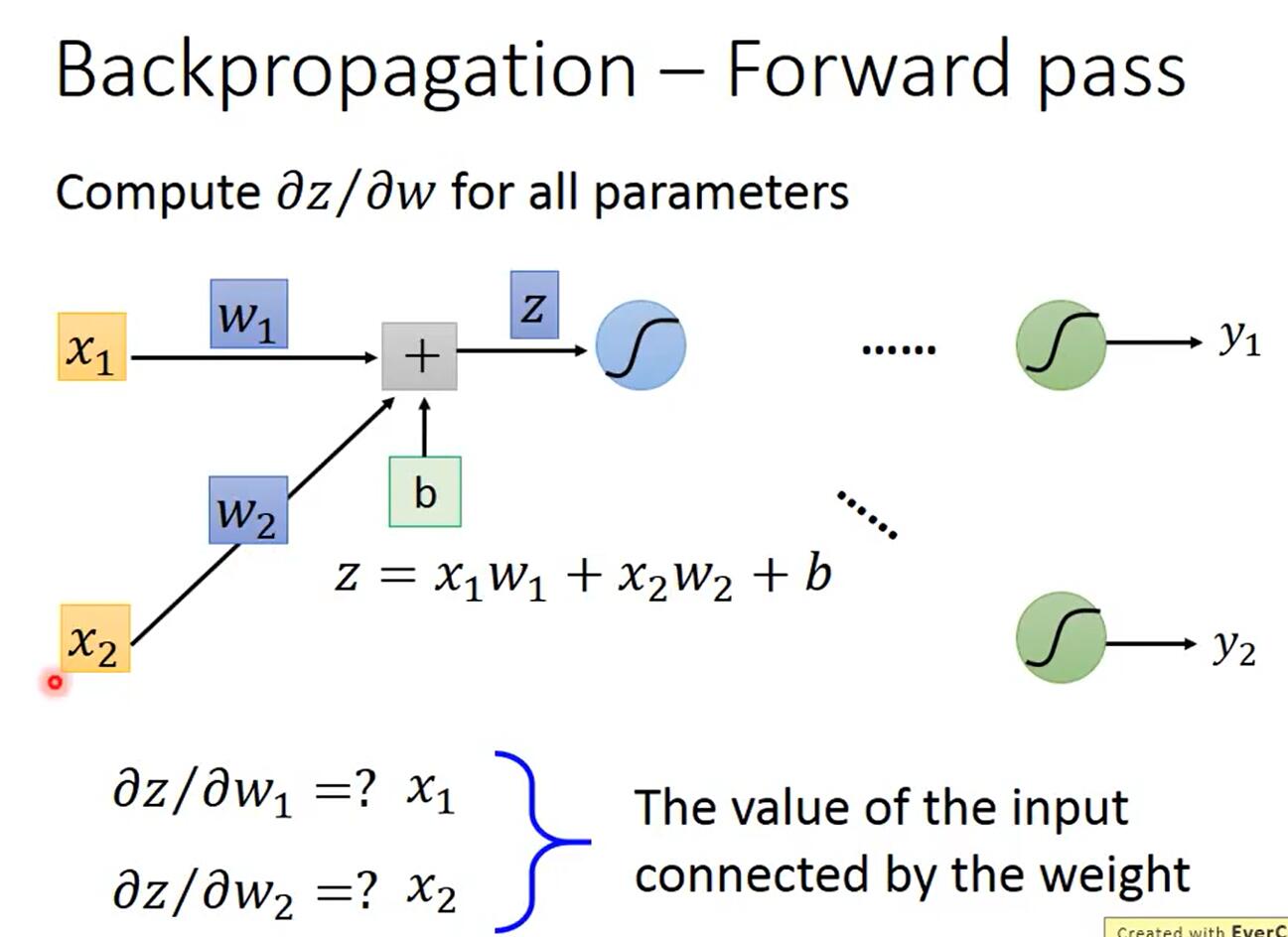
規律是:該權重乘以的那個輸入的值。所以當有多個神經元時,如下圖所示。

Backward Pass
Backward Pass是為所有激活函數的輸入\(z\)計算\(\frac{\partial C}{\partial z}\),它的方向是從後往前算的,要先算出輸出層的\(\frac{\partial C}{\partial z}\),再往前計算其它神經元的\(\frac{\partial C}{\partial z}\),所以叫Backward Pass。

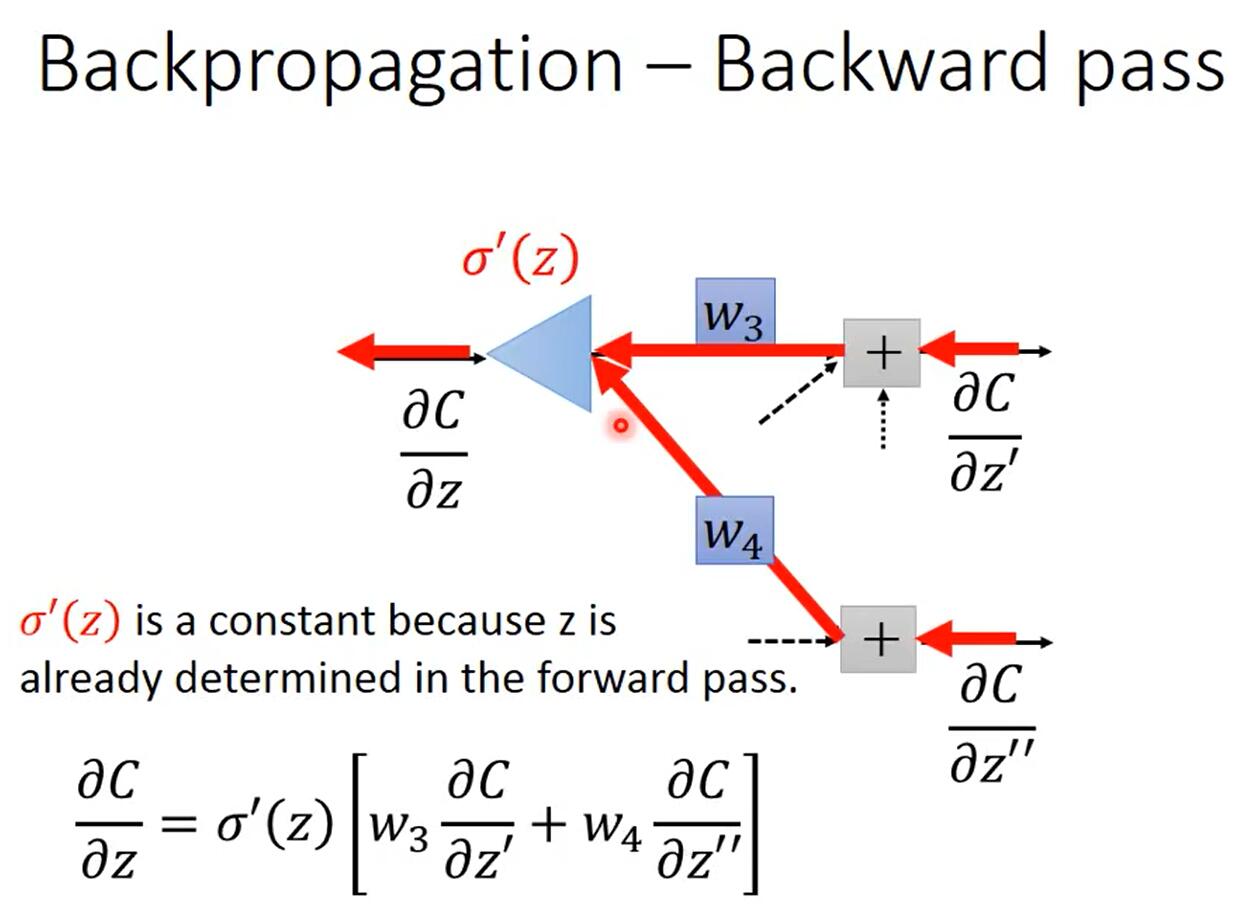
如上圖所示,令\(a=\sigma(z)\),根據鏈式法則,可知\(\frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a}\),其中\(\frac{\partial a}{\partial z}=\sigma'(z)\)是一個常數,因為在Forward Pass時\(z\)的值就已經確定了,而\(\frac{\partial C}{\partial a}=\frac{\partial z’}{\partial a}\frac{\partial C}{\partial z’}+\frac{\partial z”}{\partial a}\frac{\partial C}{\partial z”}=w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z”}\),所以\(\frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z”}]\)。
對於式子\(\frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z”}]\),我們可以發現兩點:
-
\(\frac{\partial C}{\partial z}\)的計算式是遞歸的,因為在計算\(\frac{\partial C}{\partial z}\)的時候需要計算\(\frac{\partial C}{\partial z’}\)和\(\frac{\partial C}{\partial z”}\)。
如下圖所示,輸出層的\(\frac{\partial C}{\partial z’}\)和\(\frac{\partial C}{\partial z”}\)是容易計算的。
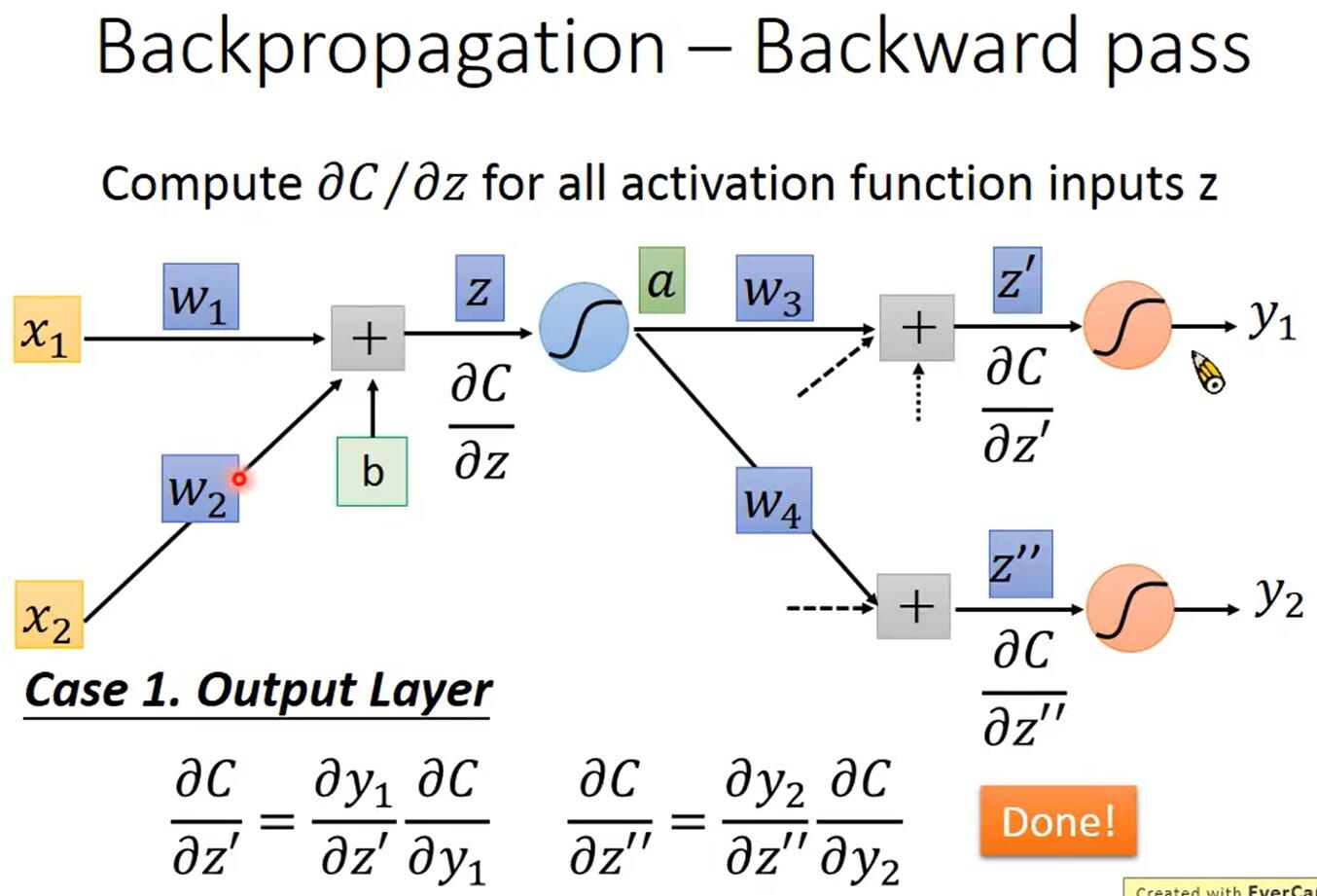
-
\(\frac{\partial C}{\partial z}\)的計算式\(\frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z’}+w_4\frac{\partial C}{\partial z”}]\)是一個神經元的形式
如下圖所示,只不過沒有嵌套sigmoid函數而是乘以一個常數\(\sigma'(z)\),每個\(\frac{\partial C}{\partial z}\)都是一個神經元的形式,所以可以通過神經網路計算\(\frac{\partial C}{\partial z}\)。
總結
- 通過Forward Pass,為所有參數\(w\)計算\(\frac{\partial z}{\partial w}\);
- 通過Backward Pass,為所有激活函數的輸入\(z\)計算\(\frac{\partial C}{\partial z}\);
- 最後\(\frac{\partial C}{\partial w}=\frac{\partial C}{\partial z}\frac{\partial z}{\partial w}\),也就求出了梯度。
Github(github.com):@chouxianyu
Github Pages(github.io):@臭鹹魚
知乎(zhihu.com):@臭鹹魚
部落格園(cnblogs.com):@臭鹹魚
B站(bilibili.com):@絕版臭鹹魚
微信公眾號:@臭鹹魚的快樂生活
轉載請註明出處,歡迎討論和交流!




