JavaScript 數據結構與演算法之美 – 非線性表中的樹、堆是幹嘛用的 ?其數據結構是怎樣的 ?
- 2019 年 10 月 3 日
- 筆記

1. 前言
想學好前端,先練好內功,內功不行,就算招式練的再花哨,終究成不了高手。
非線性表(樹、堆),可以說是前端程式設計師的內功,要知其然,知其所以然。
筆者寫的 JavaScript 數據結構與演算法之美 系列用的語言是 JavaScript ,旨在入門數據結構與演算法和方便以後複習。
非線性表中的樹、堆是幹嘛用的 ?其數據結構是怎樣的 ?
希望大家帶著這兩個問題閱讀下文。
2. 樹
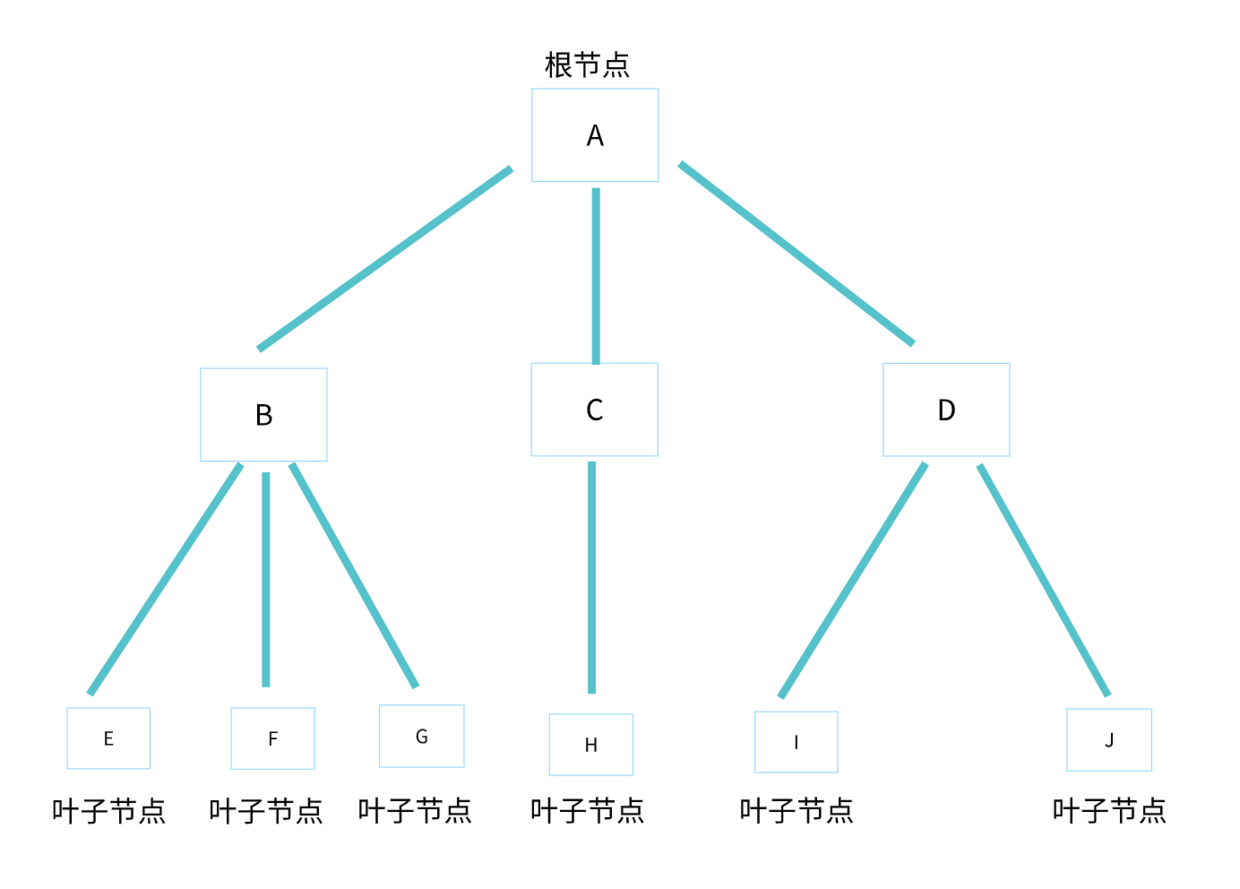
樹的數據結構就像我們生活中的真實的樹,只不過是倒過來的形狀。
術語定義
- 節點:樹中的每個元素稱為節點,如 A、B、C、D、E、F、G、H、I、J。
- 父節點:指向子節點的節點,如 A。
- 子節點:被父節點指向的節點,如 A 的孩子 B、C、D。
- 父子關係:相鄰兩節點的連線,稱為父子關係,如 A 與 B,C 與 H,D 與 J。
- 根節點:沒有父節點的節點,如 A。
- 葉子節點:沒有子節點的節點,如 E、F、G、H、I、J。
- 兄弟節點:具有相同父節點的多個節點稱為兄弟節點,如 B、C、D。
- 節點的高度:節點到葉子節點的
最長路徑所包含的邊數。 - 節點的深度:根節點到節點的路徑所包含的邊數。
- 節點層數:節點的深度 +1(根節點的層數是 1 )。
- 樹的高度:等於根節點的高度。
- 森林: n 棵互不相交的樹的集合。

高度是從下往上度量,比如一個人的身高 180cm ,起點就是從 0 開始的。
深度是從上往下度量,比如泳池的深度 180cm ,起點也是從 0 開始的。
高度和深度是帶有度字的,都是從 0 開始計數的。
而層數的計算,是和我們平時的樓層的計算是一樣的,最底下那層是第 1 層,是從 1 開始計數的,所以根節點位於第 1 層,其他子節點依次加 1。
二叉樹分類
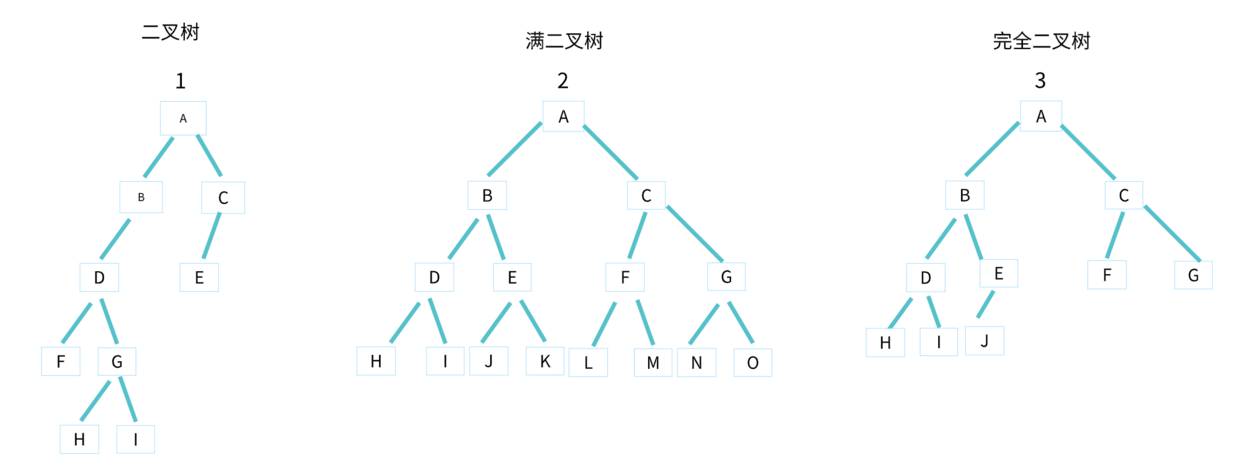
二叉樹
- 每個節點
最多只有2 個子節點的樹,這兩個節點分別是左子節點和右子節點。如上圖中的 1、 2、3。
不過,二叉樹並不要求每個節點都有兩個子節點,有的節點只有左子節點,有的節點只有右子節點。以此類推,自己想四叉樹、八叉樹的結構圖。
滿二叉樹
- 一種特殊的二叉樹,除了葉子節點外,每個節點
都有左右兩個子節點,這種二叉樹叫做滿二叉樹。如上圖中的 2。
完全二叉樹
- 一種特殊的二叉樹,葉子節點都在最底下兩層,最後一層葉子節都靠
左排列,並且除了最後一層,其他層的節點個數都要達到最大,這種二叉樹叫做完全二叉樹。如上圖的 3。
完全二叉樹與不是完全二叉樹的區分比較難,所以對比下圖看看。
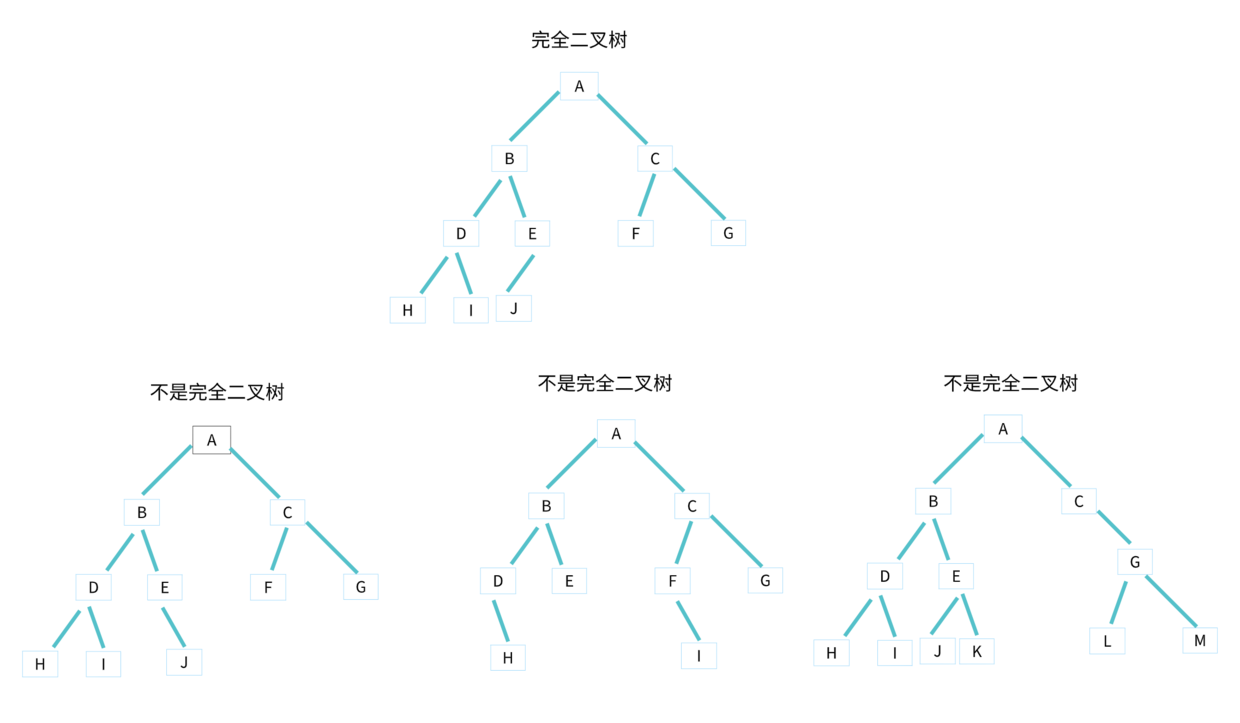
堆
之前的文章 棧記憶體與堆記憶體 、淺拷貝與深拷貝 中有說到:JavaScript 中的引用類型(如對象、數組、函數等)是保存在堆記憶體中的對象,值大小不固定,棧記憶體中存放的該對象的訪問地址指向堆記憶體中的對象,JavaScript 不允許直接訪問堆記憶體中的位置,因此操作對象時,實際操作對象的引用。
那麼堆到底是什麼呢 ?其數據結構又是怎樣的呢 ?
堆其實是一種特殊的樹。只要滿足這兩點,它就是一個堆。
- 堆是一個完全二叉樹。
完全二叉樹:除了最後一層,其他層的節點個數都是滿的,最後一層的節點都靠左排列。 - 堆中每一個節點的值都必須大於等於(或小於等於)其子樹中每個節點的值。
也可以說:堆中每個節點的值都大於等於(或者小於等於)其左右子節點的值。這兩種表述是等價的。
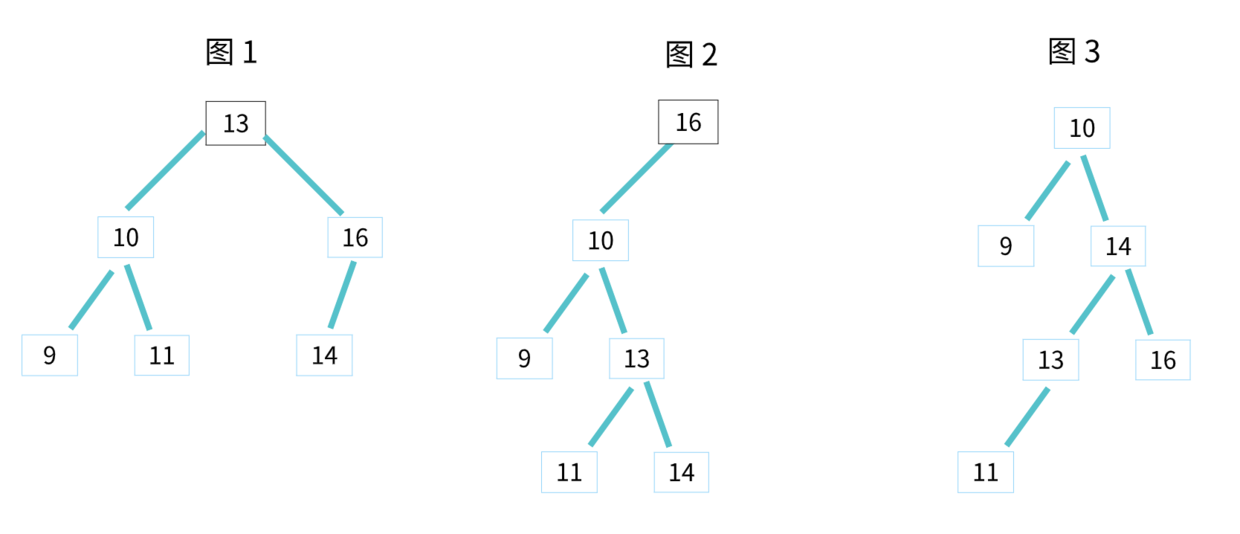
對於每個節點的值都大於等於子樹中每個節點值的堆,我們叫作大頂堆。對於每個節點的值都小於等於子樹中每個節點值的堆,我們叫作小頂堆。
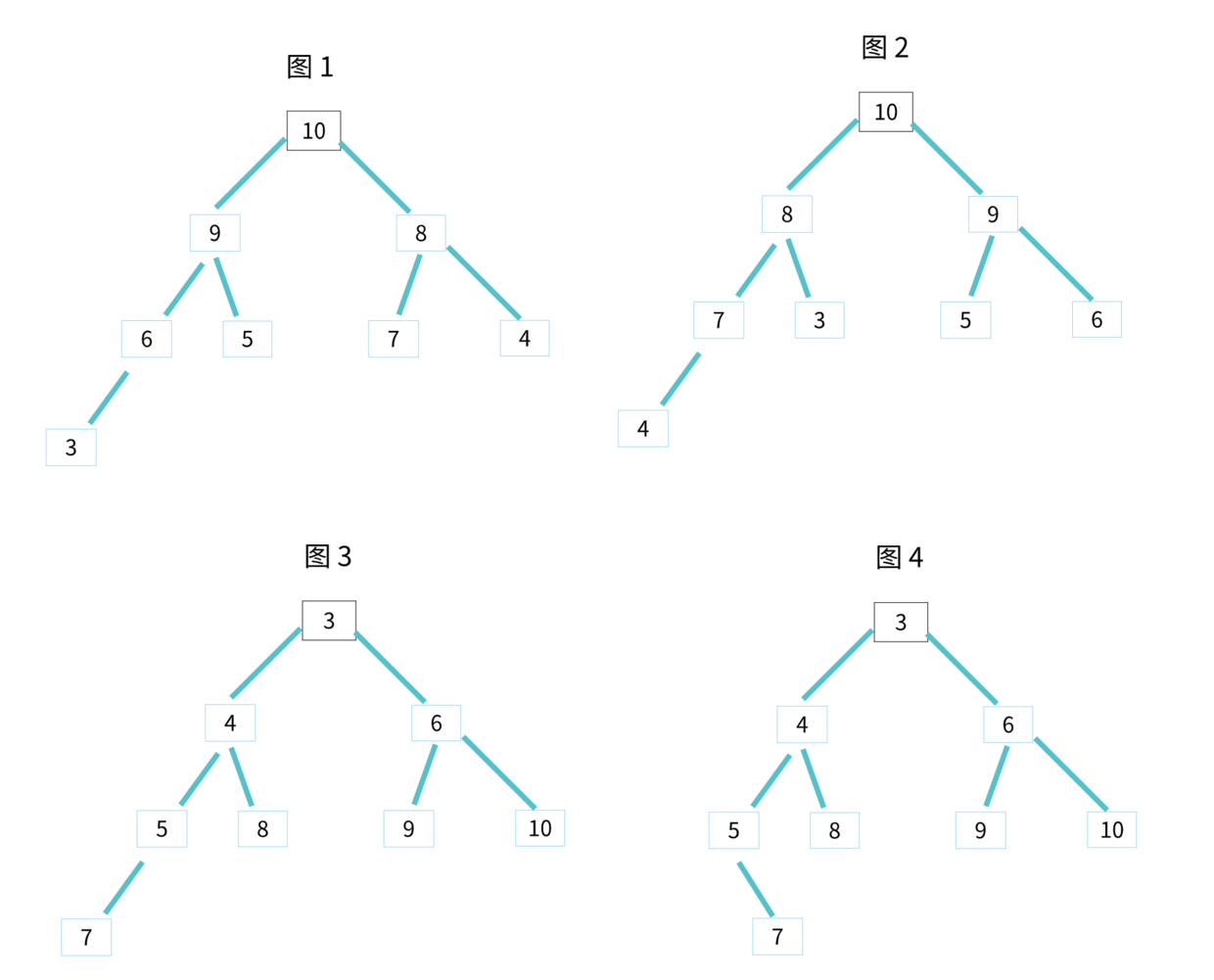
其中圖 1 和 圖 2 是大頂堆,圖 3 是小頂堆,圖 4 不是堆。除此之外,從圖中還可以看出來,對於同一組數據,我們可以構建多種不同形態的堆。
二叉查找樹(Binary Search Tree)
- 一種特殊的二叉樹,相對
較小的值保存在左節點中,較大的值保存在右節點中,叫二叉查找樹,也叫二叉搜索樹。
二叉查找樹是一種有序的樹,所以支援快速查找、快速插入、刪除一個數據。
下圖中, 3 個都是二叉查找樹,
平衡二叉查找樹
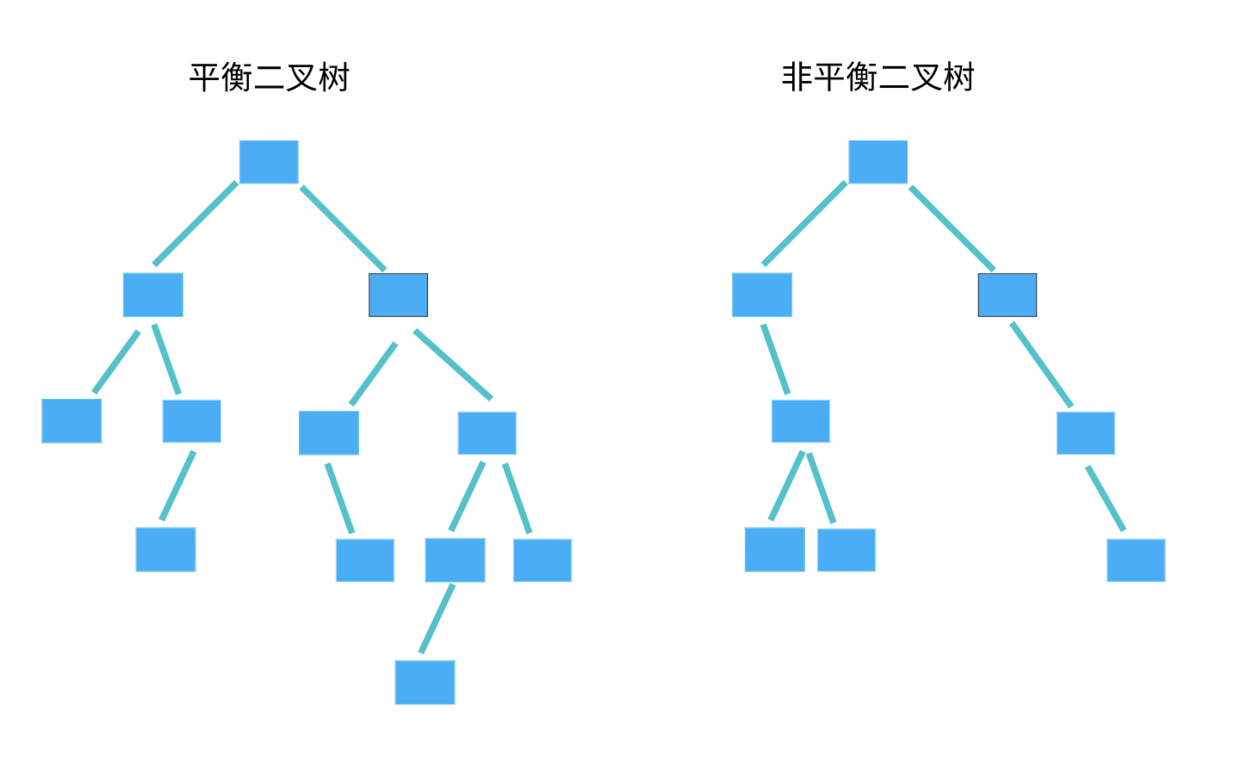
- 平衡二叉查找樹:二叉樹中任意一個節點的左右子樹的高度相差不能大於 1。
從這個定義來看,完全二叉樹、滿二叉樹其實都是平衡二叉樹,但是非完全二叉樹也有可能是平衡二叉樹。
平衡二叉查找樹中平衡的意思,其實就是讓整棵樹左右看起來比較對稱、比較平衡,不要出現左子樹很高、右子樹很矮的情況。這樣就能讓整棵樹的高度相對來說低一些,相應的插入、刪除、查找等操作的效率高一些。
平衡二叉查找樹其實有很多,比如,Splay Tree(伸展樹)、Treap(樹堆)等,但是我們提到平衡二叉查找樹,聽到的基本都是紅黑樹。
紅黑樹(Red-Black Tree)
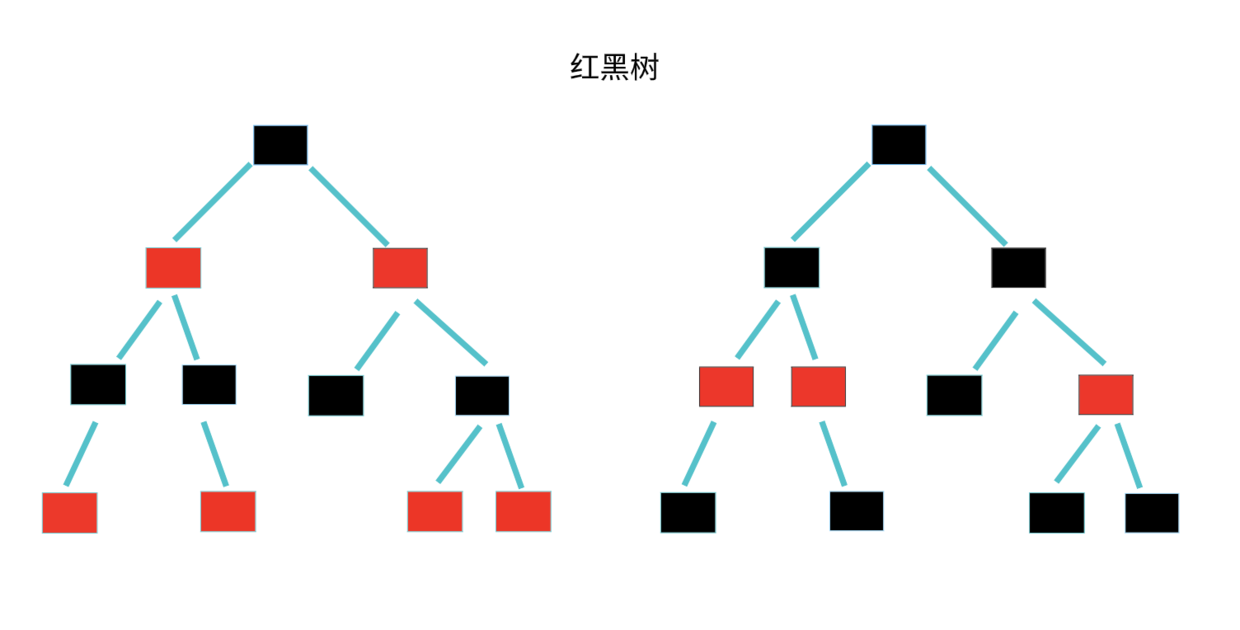
紅黑樹中的節點,一類被標記為黑色,一類被標記為紅色。除此之外,一棵紅黑樹還需要滿足這樣幾個要求:
- 根節點是黑色的。
- 每個葉子節點都是黑色的空節點(NIL),也就是說,葉子節點不存儲數據。
- 任何相鄰的節點都不能同時為紅色,也就是說,紅色節點是被黑色節點隔開的。
- 每個節點,從該節點到達其可達葉子節點的所有路徑,都包含相同數目的黑色節點。
下面兩個都是紅黑樹。
存儲
完全二叉樹的存儲
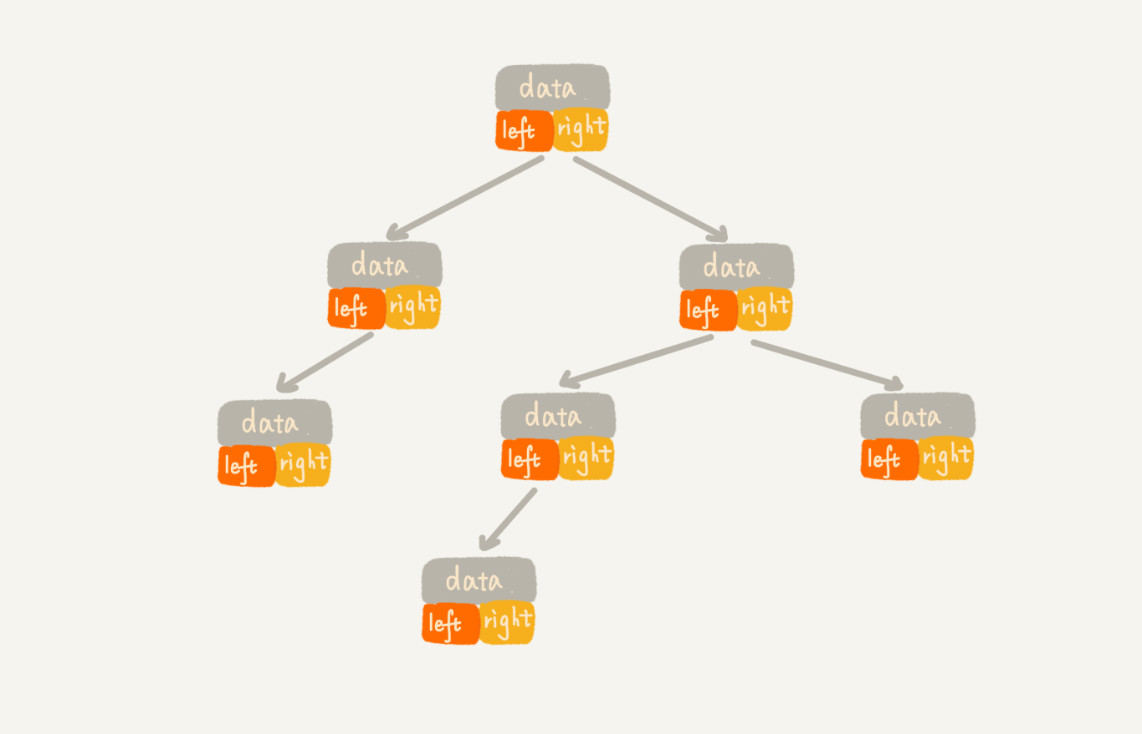
- 鏈式存儲
每個節點由 3 個欄位,其中一個存儲數據,另外兩個是指向左右子節點的指針。
我們只要拎住根節點,就可以通過左右子節點的指針,把整棵樹都串起來。
這種存儲方式比較常用,大部分二叉樹程式碼都是通過這種方式實現的。
- 順序存儲
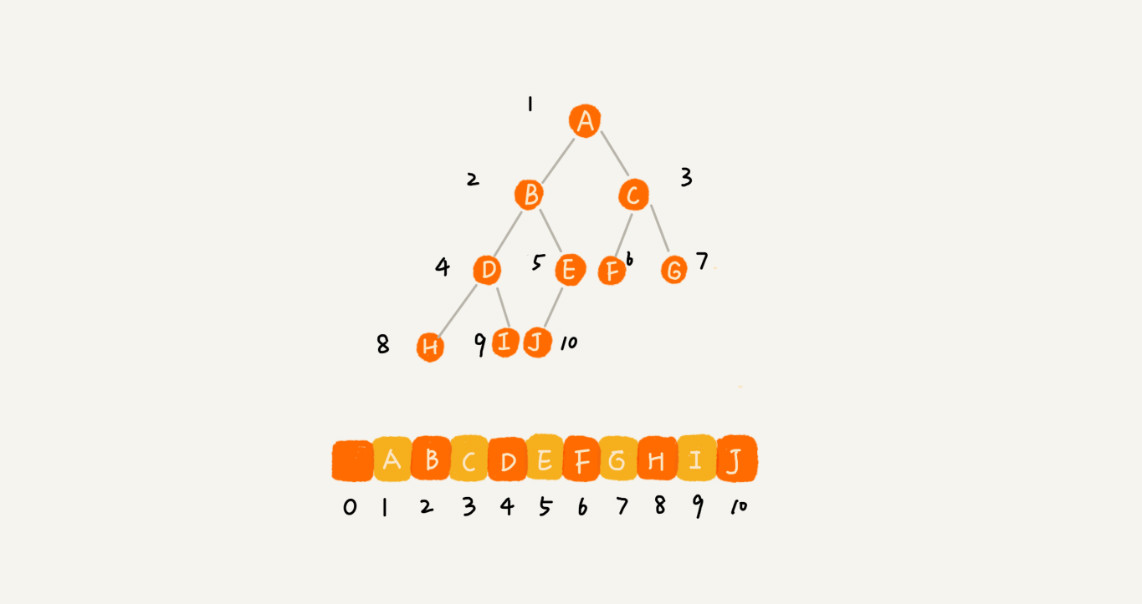
用數組來存儲,對於完全二叉樹,如果節點 X 存儲在數組中的下標為 i ,那麼它的左子節點的存儲下標為 2 * i ,右子節點的下標為 2 * i + 1,反過來,下標 i / 2 位置存儲的就是該節點的父節點。
注意,根節點存儲在下標為 1 的位置。完全二叉樹用數組來存儲是最省記憶體的方式。
二叉樹的遍歷
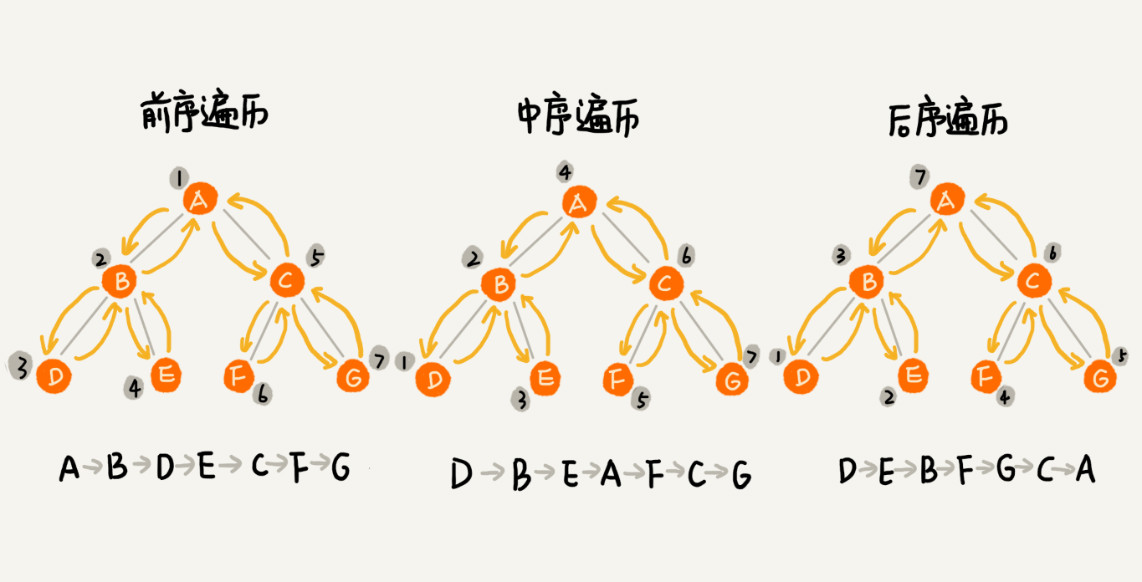
經典的方法有三種:前序遍歷、中序遍歷、後序遍歷。其中,前、中、後序,表示的是節點與它的左右子樹節點遍歷訪問的先後順序。
前序遍歷(根 => 左 => 右)
- 對於樹中的任意節點來說,先訪問這個節點,然後再訪問它的左子樹,最後訪問它的右子樹。
中序遍歷(左 => 根 => 右)
- 對於樹中的任意節點來說,先訪問它的左子樹,然後再訪問它的本身,最後訪問它的右子樹。
後序遍歷(左 => 右 => 根)
- 對於樹中的任意節點來說,先訪問它的左子樹,然後再訪問它的右子樹,最後訪問它本身。
實際上,二叉樹的前、中、後序遍歷就是一個遞歸的過程。
時間複雜度:3 種遍歷方式中,每個節點最多會被訪問 2 次,跟節點的個數 n 成正比,所以時間複雜度是 O(n)。
實現二叉查找樹
二叉查找樹的特點是:相對較小的值保存在左節點中,較大的值保存在右節點中。
程式碼實現二叉查找樹,方法有以下這些。
方法
- insert(key):向樹中插入一個新的鍵。
- search(key):在樹中查找一個鍵,如果節點存在,則返回 true;如果不存在,則返回 false。
- min:返回樹中最小的值/鍵。
- max:返回樹中最大的值/鍵。
- remove(key):從樹中移除某個鍵。
遍歷
- preOrderTraverse:通過
先序遍歷方式遍歷所有節點。 - inOrderTraverse:通過
中序遍歷方式遍歷所有節點。 - postOrderTraverse:通過
後序遍歷方式遍歷所有節點。
具體程式碼
- 首先實現二叉查找樹類的類
// 二叉查找樹類 function BinarySearchTree() { // 用於實例化節點的類 var Node = function(key){ this.key = key; // 節點的健值 this.left = null; // 指向左節點的指針 this.right = null; // 指向右節點的指針 }; var root = null; // 將根節點置為null }- insert 方法,向樹中插入一個新的鍵。
遍歷樹,將插入節點的鍵值與遍歷到的節點鍵值比較,如果前者大於後者,繼續遞歸遍歷右子節點,反之,繼續遍歷左子節點,直到找到一個空的節點,在該位置插入。
this.insert = function(key){ var newNode = new Node(key); // 實例化一個節點 if (root === null){ root = newNode; // 如果樹為空,直接將該節點作為根節點 } else { insertNode(root,newNode); // 插入節點(傳入根節點作為參數) } }; // 插入節點的函數 var insertNode = function(node, newNode){ // 如果插入節點的鍵值小於當前節點的鍵值 // (第一次執行insertNode函數時,當前節點就是根節點) if (newNode.key < node.key){ if (node.left === null){ // 如果當前節點的左子節點為空,就直接在該左子節點處插入 node.left = newNode; } else { // 如果左子節點不為空,需要繼續執行insertNode函數, // 將要插入的節點與左子節點的後代繼續比較,直到找到能夠插入的位置 insertNode(node.left, newNode); } } else { // 如果插入節點的鍵值大於當前節點的鍵值 // 處理過程類似,只是insertNode函數繼續比較的是右子節點 if (node.right === null){ node.right = newNode; } else { insertNode(node.right, newNode); } } }在下圖的樹中插入健值為 6 的節點,過程如下:
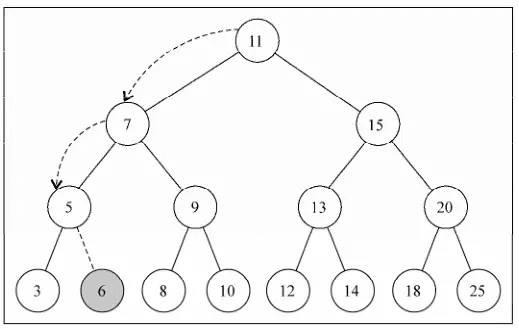
- 搜索最小值
在二叉搜索樹里,不管是整個樹還是其子樹,最小值一定在樹最左側的最底層。
因此給定一顆樹或其子樹,只需要一直向左節點遍歷到底就行了。
this.min = function(node) { // min方法允許傳入子樹 node = node || root; // 一直遍歷左側子節點,直到底部 while (node && node.left !== null) { node = node.left; } return node; };- 搜索最大值
搜索最大值與搜索最小值類似,只是沿著樹的右側遍歷。
this.max = function(node) { // min方法允許傳入子樹 node = node || root; // 一直遍歷左側子節點,直到底部 while (node && node.right !== null) { node = node.right; } return node; };- 搜索特定值
搜索特定值的處理與插入值的處理類似。遍歷樹,將要搜索的值與遍歷到的節點比較,如果前者大於後者,則遞歸遍歷右側子節點,反之,則遞歸遍歷左側子節點。
this.search = function(key, node){ // 同樣的,search方法允許在子樹中查找值 node = node || root; return searchNode(key, node); }; var searchNode = function(key, node){ // 如果node是null,說明樹中沒有要查找的值,返回false if (node === null){ return false; } if (key < node.key){ // 如果要查找的值小於該節點,繼續遞歸遍歷其左側節點 return searchNode(node.left, key); } else if (key > node.key){ // 如果要查找的值大於該節點,繼續遞歸遍歷其右側節點 return searchNode(node.right, key); } else { // 如果要查找的值等於該節點,說明查找成功,返回改節點 return node; } };- 移除節點
移除節點,首先要在樹中查找到要移除的節點,再判斷該節點是否有子節點、有一個子節點或者有兩個子節點,最後分別處理。
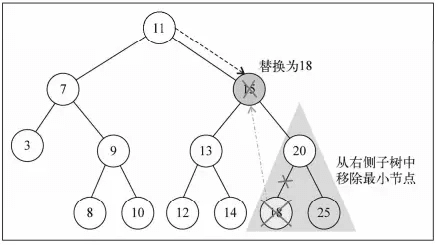
this.remove = function(key, node) { // 同樣的,允許僅在子樹中刪除節點 node = node || root; return removeNode(key, node); }; var self = this; var removeNode = function(key, node) { // 如果 node 不存在,直接返回 if (node === false) { return null; } // 找到要刪除的節點 node = self.search(key, node); // 第一種情況,該節點沒有子節點 if (node.left === null && node.right === null) { node = null; return node; } // 第二種情況,該節點只有一個子節點的節點 if (node.left === null) { // 只有右節點 node = node.right; return node; } else if (node.right === null) { // 只有左節點 node = node.left; return node; } // 第三種情況,有有兩個子節點的節點 // 將右側子樹中的最小值,替換到要刪除的位置 // 找到最小值 var aux = self.min(node.right); // 替換 node.key = aux.key; // 刪除最小值 node.right = removeNode(aux.key, node.right); return node; };第三種情況的處理過程,如下圖所示。
當要刪除的節點有兩個子節點時,為了不破壞樹的結構,刪除後要替補上來的節點的鍵值大小必須在已刪除節點的左、右子節點的鍵值之間,且替補上來的節點不應該有子節點,否則會產生一個節點有多個位元組點的情況,因此,找右側子樹的最小值替換上來。
同理,找左側子樹的最大值替換上來也可以。
- 先序遍歷
this.preOrderTraverse = function(callback){ // 同樣的,callback用於對遍歷到的節點做操作 preOrderTraverseNode(root, callback); }; var preOrderTraverseNode = function (node, callback) { // 遍歷到node為null為止 if (node !== null) { callback(node.key); // 先處理當前節點 preOrderTraverseNode(node.left, callback); // 再繼續遍歷左子節點 preOrderTraverseNode(node.right, callback); // 最後遍歷右子節點 } };用先序遍歷遍歷下圖所示的樹,並列印節點鍵值。
輸出結果:11 7 5 3 6 9 8 10 15 13 12 14 20 18 25。
遍歷過程如圖:

- 中序遍歷
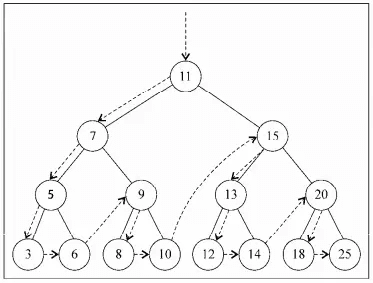
this.inOrderTraverse = function(callback){ // callback用於對遍歷到的節點做操作 inOrderTraverseNode(root, callback); }; var inOrderTraverseNode = function (node, callback) { // 遍歷到node為null為止 if (node !== null) { // 優先遍歷左邊節點,保證從小到大遍歷 inOrderTraverseNode(node.left, callback); // 處理當前的節點 callback(node.key); // 遍歷右側節點 inOrderTraverseNode(node.right, callback); } };對下圖的樹做中序遍歷,並輸出各個節點的鍵值。
依次輸出:3 5 6 7 8 9 10 11 12 13 14 15 18 20 25。
遍歷過程如圖:
- 後序遍歷
this.postOrderTraverse = function(callback){ postOrderTraverseNode(root, callback); }; var postOrderTraverseNode = function (node, callback) { if (node !== null) { postOrderTraverseNode(node.left, callback); //{1} postOrderTraverseNode(node.right, callback); //{2} callback(node.key); //{3} } };可以看到,中序、先序、後序遍歷的實現方式幾乎一模一樣,只是 {1}、{2}、{3} 行程式碼的執行順序不同。
對下圖的樹進行後序遍歷,並列印鍵值:3 6 5 8 10 9 7 12 14 13 18 25 20 15 11。
遍歷過程如圖:

- 添加列印的方法 print。
this.print = function() { console.log('root :', root); return root; };完整程式碼請看文件 binary-search-tree.html
測試過程:
// 測試 var binarySearchTree = new BinarySearchTree(); var arr = [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25]; for (var i = 0; i < arr.length; i++) { var value = arr[i]; binarySearchTree.insert(value); } console.log('先序遍歷:'); var arr = []; binarySearchTree.preOrderTraverse(function(value) { // console.log(value); arr.push(value); }); console.log('arr :', arr); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 13, 12, 14, 20, 18, 25] var min = binarySearchTree.min(); console.log('min:', min); // 3 var max = binarySearchTree.max(); console.log('max:', max); // 25 var search = binarySearchTree.search(10); console.log('search:', search); // 10 var remove = binarySearchTree.remove(13); console.log('remove:', remove); // 13 console.log('先序遍歷:'); var arr1 = []; binarySearchTree.preOrderTraverse(function(value) { // console.log(value); arr1.push(value); }); console.log('arr1 :', arr1); // [11, 7, 5, 3, 6, 9, 8, 10, 15, 14, 12, 20, 18, 25] console.log('中序遍歷:'); var arr2 = []; binarySearchTree.inOrderTraverse(function(value) { // console.log(value); arr2.push(value); }); console.log('arr2 :', arr2); // [3, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 18, 20, 25] console.log('後序遍歷:'); var arr3 = []; binarySearchTree.postOrderTraverse(function(value) { // console.log(value); arr3.push(value); }); console.log('arr3 :', arr3); // [3, 6, 5, 8, 10, 9, 7, 12, 14, 18, 25, 20, 15, 11] binarySearchTree.print(); // 看控制台結果如下:
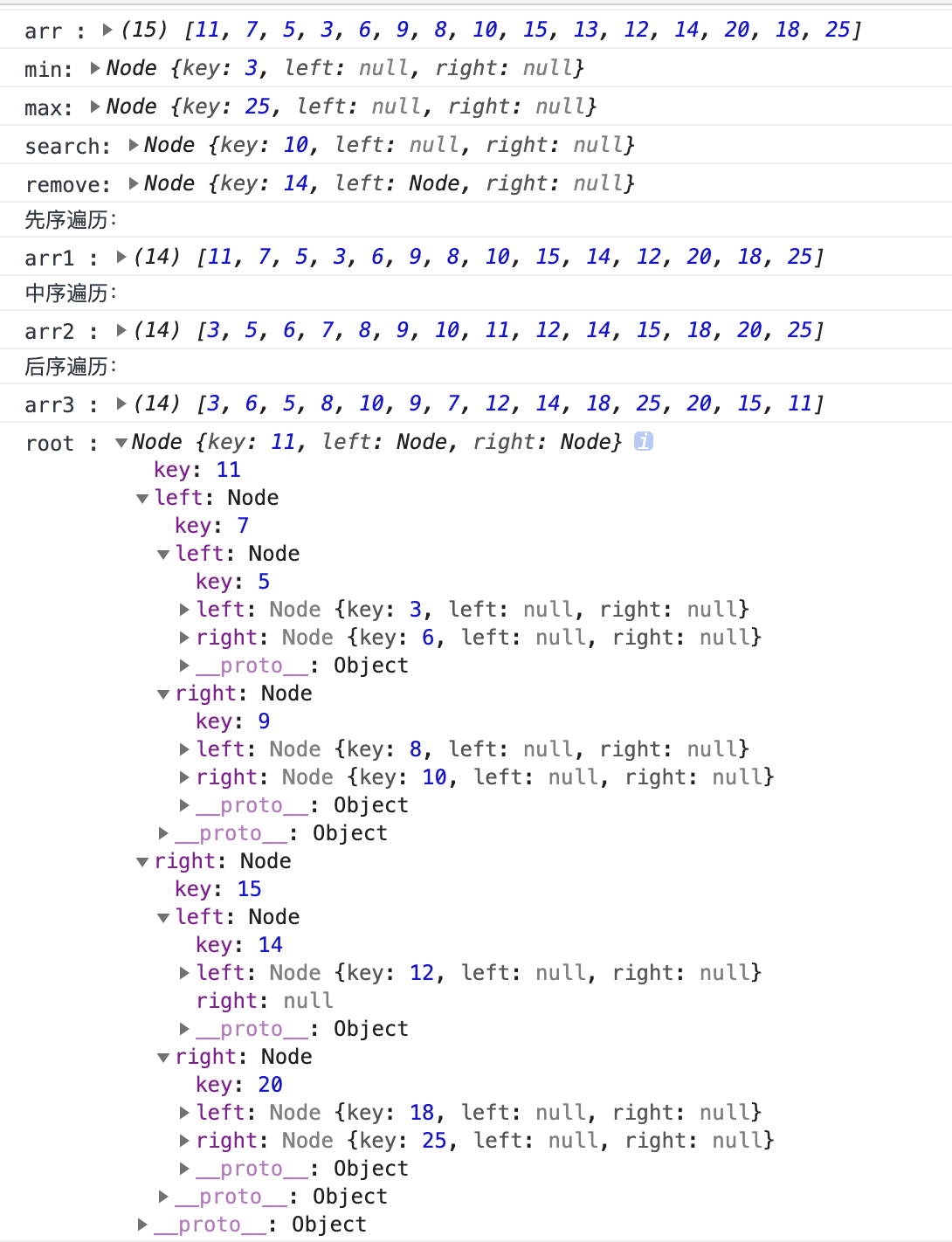
看到這裡,你能解答文章的題目 非線性表中的樹、堆是幹嘛用的 ?其數據結構是怎樣的 ?
如果不能,建議再回頭仔細看看哦。
3. 最後
如果覺得本文還不錯,記得給個 star , 你的 star 是我持續更新的動力。
筆者 GitHub。
參考文章:
