人工智慧必備數學基礎：線性代數基礎（1）

2021 年 1 月 8 日
筆記
人工智慧必備數學基礎

如果需要小編其他數學基礎部落格，請移步小編的GitHub地址

　　傳送門：請點擊我

　　如果點擊有誤：//github.com/LeBron-Jian/DeepLearningNote

　　這裡我打算再補充一下關於線性代數的基礎。

　　（注意：目前自己補充到的所有知識點，均按照自己網課影片中老師課程知識點走的，同時一些公式是網友辛辛苦苦敲的，這裡用到那個部落格均在文末補充地址，不過這裡首先表示感謝！！）

1，行列式

1.1 行列式的定義

　　行列式在數學中，是一個函數，其定義域為det的矩陣A，取值為一個標量，寫作 det(A) 或 |A|。無論是在線性代數，多項式理論，還是微積分學中（比如換元積分法），行列式作為基本的數學工具，都有著重要的應用。

　　下面先看看二次線性方程組的求解：

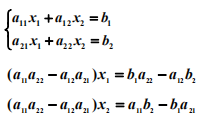
　　當 a₁₁a₂₂– a₁₂a₂₁ ≠ 0 方程組有唯一解：

　　我們看行列式，發現其好像有點規律：

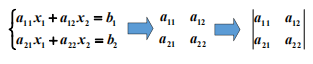　　表達式 a₁₁a₂₂– a₁₂a₂₁ 即為二階行列式。

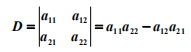
　　其中 a_ij (i=1,2；j=1,2) 稱為元素。 i 代表行標， j 代表列標。

　　三階行列式如下：

　　所以可以得到行列式的定義為：n階行列式是由 n 階方陣形式的 n² 個數 a_ij（i,j=1,2,…n）確定的一個數，其值為 n!項之和。若n階方陣A=(aij)，則A相應的行列式D記為：D=|A|=detA=det(aij)；若矩陣A相應的行列式D=0，稱A為奇異矩陣，否則稱為非奇異矩陣。

　　下面嘗試計算一個三階行列式，根據如上演算法，計算過程如下：

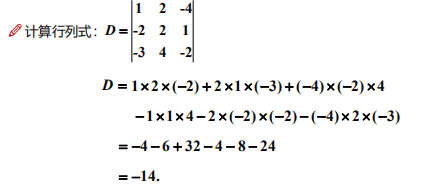
1.2 行列式的性質

1，行列式A中某行（或者列）用同一數 k 乘，其結果等於 kA
2，行列式A等於其轉置行列式A^T（A^T的第i行為A的第i列）
3，若 n 階行列式 |a_ij| 中某行（或列）；行列式則 |aij| 是兩個行列式的和，這兩個行列式的第 i 行（或列），一個是 b1, b2,…bn，另一個是 c1, c2,…cn，其餘各行（或列）上的元與 |aij| 的完全一樣
4，行列式A中兩行（或列）互換，其結果等於-A
5，把行列式A的某行（或列）中各元同乘一數後加到另一行（或列）中對應元上，結果仍然是A

1.3 矩陣與數據之間的關係

　　我們學習矩陣的目的，最終是要應用到機器學習，而不是單純的學習數學推導，下面看矩陣和數據之間關係。

　　比如A，B，C，D 代表四座城市，他們之間可通行的關係為：

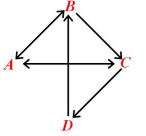
　　如果有表格的形式表示，則表示如下：

2，矩陣

2.1 矩陣的定義

　　在數學中，矩陣（Matrix）是一個按照長方陣列排列的複數或實數集合，最早來自於方程組的係數及常數所構成的方陣，這一概念由19世紀英國數學家凱里首先提出。

　　何謂矩陣就是輸入的數據就是矩陣，對數據做任何的操作都是矩陣的操作。

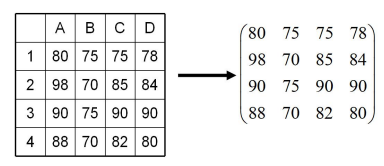　　定義：矩陣是由行和列組成的，即 m*n 個數 aij 排成 m 行 n 列的表格稱為矩陣，簡記為 A，或者（a_ij）_m*n，若 m = n，則稱A是 n 階矩陣或 n 階方陣，矩陣如下：

　　元素是實數的矩陣稱為實矩陣，元素是複數的矩陣稱為復矩陣

矩陣的特殊形式

　　行向量和列向量：

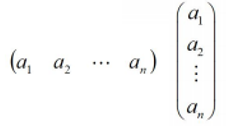
　　n階矩陣（n階方陣）：n階方陣就是行和列一樣，即 m=n，我們稱A為 n 階矩陣或 n 階方陣：

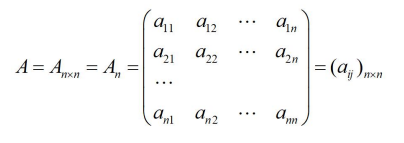
　　三角矩陣（上三角矩陣與下三角矩陣）：在線性代數中，三角矩陣是方形矩陣的一種，因其非零係數的排列呈三角形狀而得名。三角矩陣分為上三角和下三角。若i>j，則 uij=0的矩陣稱為上三角矩陣；若i<j，則 uij=0的矩陣稱為下三角矩陣。

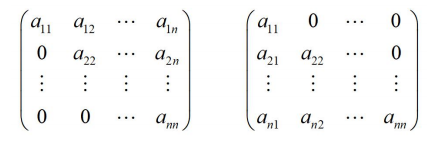
　　對角陣與單位矩陣：（對角矩陣是對於m*m的居住，當i!=j時，有aij=0，此時所有非對角線上的元素均為0，此時的矩陣稱為對角矩陣，當對角線的元素為1時，稱為單位矩陣。）

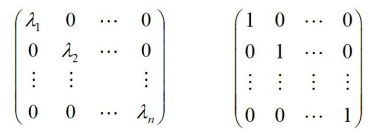　　同型矩陣：兩個矩陣行列數相同的時候：

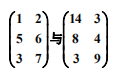
　　在同型的前提下，並且各個元素相等，這就是矩陣相等了：

　　對稱矩陣：如果滿足 A^T = A ，那麼 A就是對稱矩陣。

　　如下行列式，均為對稱矩陣：

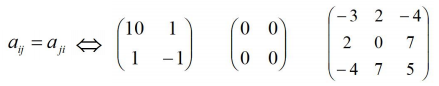
2.2 矩陣的線性運算

　　矩陣運算在科學計算中非常重要，而矩陣的基本運算包括矩陣的加法，減法，數乘，轉置，共軛和共軛轉置。

　　下面通過兩個 m*n 的矩陣來看一下其基本運算： A = (a_ij)，B = (b_ij)

矩陣的加減法

　　設 A = (a_ij) ，B = (b_ij) 是兩個 m*n 矩陣，則 m*n 矩陣 C = (c_ij) = a_ij + b_ij ，稱為矩陣 A 和 B 的和，記為 A + B = C。

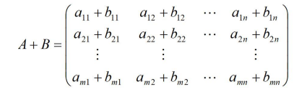
　　矩陣的加法滿足以下運算律（A，B，C都是同型矩陣）：

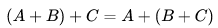
　　應該注意的是只有同型矩陣之間才可以進行加法。

矩陣的數乘

　　設 A = (a_ij) 是 m*n 矩陣，k 是一個常數，則 m*n 矩陣 (ka_ij) 稱為數 k 與矩陣 A 的數乘，記為 kA ，如下：

　　矩陣的數乘滿足以下運算律：

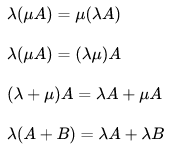
　　矩陣的加減法和矩陣的數乘合成矩陣的線性運算。

2.3 矩陣的轉置

　　矩陣的轉置就是行和列互相交換所產生的矩陣，記做A^T，如下：

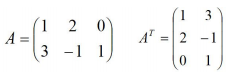
　　矩陣的轉置有如下性質：

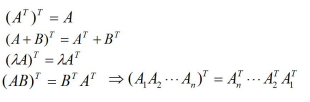
2.4 矩陣的逆

　　有關 A-1 的結論：

　　分塊求逆公式：

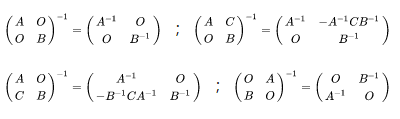
　　這裡 A， B 均為可逆方陣。

2.5 矩陣的秩

　　對於一個 S*N 的矩陣：

　　矩陣 A 的每一行可以看作一個 N 維向量：

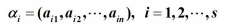
　　α₁， α₂， … α_s 叫做 A 的行向量。

　　矩陣 A的每一列可以看作一個 S 維向量：

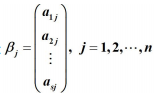
　　β₁， β₂， … β_n 叫做 A的列向量。

　　矩陣的秩表示什麼呢？

　　對於下面的A矩陣：

　　行向量為：

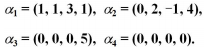　　求其極大線性無關組假設有：

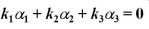
　　則：

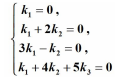
　　解得： k1 = k2 = k3 = 0，即 α₁， α₂， α₃ 線性無關。

　　由於含有零向量，必線性相關，所以向量組α₁， α₂， α₃ ，α₄ 的秩為 3。

　　對於列向量同理可得：

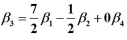
　　但是 β₁， β₂， β₃ ， β₄的秩為3。

　　矩陣的行秩 = 矩陣的列秩。

　　那麼秩該如何理解呢？

　　可以對二維影像進行旋轉，比如用旋轉矩陣：

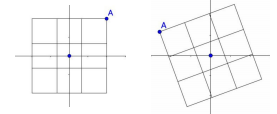
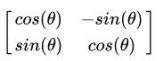　　變換後的矩陣依然是二維的，所以旋轉矩陣的秩為2，如下圖：

　　或者對於下面的矩陣：

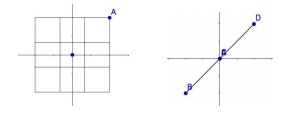
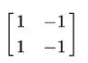　　變換後的矩陣為一維的，所以矩陣的秩為1，如下圖：

　　矩陣中最大不相關向量的個數就是秩，比如相冊里有很多張圖片（N），但是只有三個類（R），我們就把 R 當做矩陣的秩。

有關矩陣秩的結論：

2.6 矩陣的乘法

　　設 A = (a_ij) 是 m*n 矩陣，B = (b_ij) 是 n*s 矩陣，那麼 m*s 矩陣 C = (c_ij) ，C_ij稱為 AB 的乘積，記為 C = AB 。（注意兩個矩陣的乘法僅當第一個矩陣A的列數和另一個矩陣B的行數相等時才能定義）

　　其中：

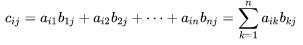
　　矩陣乘法有如下的運算規則（注意：矩陣乘法不滿足交換律）包括左分配律，右分配律，結合律：

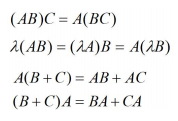
　　舉個例子：有兩個商場，三種電視機，求兩個商場的銷售額？（注意：A的列數要與B的函數相等）

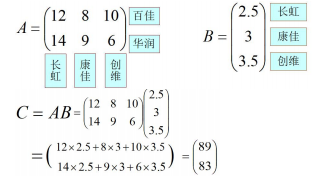　　注意：矩陣乘法沒有交換律

　　舉個簡單的例子，當我們交換的時候，會出現下面結果：

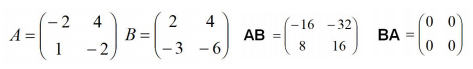
2.7 行列式與矩陣的區別

　　行列式與矩陣的區別：

　　具體區別如下：

　　1，運算結果不同

　　矩陣是一個表格，行數和列數可以不一樣；而行列式是一個數，且行數必須等於列數。只有方陣才可以定義它的行列式，而對於長方陣不能定義它的行列式。

　　兩個矩陣相等是指對應元素都相等；兩個行列式相等不要求對應元素都相等，甚至階數也可以不一樣，只要運算代數和的結果一樣就可以了。

　　2，運算方式不同

　　兩矩陣相加是將各對應元素相加；兩行列式相加，是將運算結果相加，在特殊情況下（比如有行或列相同），只能將一行（或列）的元素相加，其餘元素照寫。

　　3，性質不同

　　數乘矩陣是指該數乘以矩陣的每一個元素；而數乘行列式，只能用此數乘行列式的某一行或列，提公因數也如此。

　　兩矩陣相等指兩同型矩陣的對應元素相等；兩行列式相等指只要其值相等，不要求它們是同階行列式，也不要求對應元素相等。

　　4，變換後的結果不同

　　矩陣經初等變換，其秩不變；行列式經初等變換，其值可能改變；換法變換要變好，倍法變換差被數，消法變換不改變。

2.8 矩陣方程

　　矩陣方程如何做呢？

　　如下：A是係數矩陣，X是未知數矩陣，B是常數矩陣

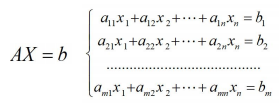
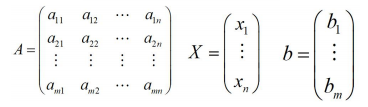
　　矩陣方程是未知數為矩陣的方程，對於矩陣方程，當係數矩陣為方陣時，先判斷是否可逆。如果可逆，則可以利用左乘或者右乘逆矩陣的方法求出未知矩陣，如果方陣不可逆或係數矩陣不是方陣，則需要用矩陣的廣義逆來確定矩陣方程有界的條件，進而在有解的情況下求出通解。

3，向量

3.1 向量的定義

　　在數學中，向量（也稱為歐幾里得向量，幾何向量，矢量），指具有大小（magnitude）和方向的量。它可以形象的表示為帶箭頭的線段。箭頭所指：代表向量的方向；線段長度：代表向量的大小。與向量對應的量叫做數量（物理學中稱為標量），數量（標量）只有大小，沒有方向。

　　在物理學和工程學中，幾何向量更常被稱為矢量。許多物理量都是矢量，比如一個物體的唯一，球撞向牆對其施加的力等等。與之相對的是標量，即只有大小沒有方向的量。一些與向量有關的定義亦與物理概念有密切的聯繫，例如向量勢對應於物理中的勢能。　

3.2 有關向量的線性表示

3.3 向量組的秩與矩陣的秩之間的關係

　　設 r(A_m*n) = r ，則 A 的秩 r(A) 與 A 的行列向量組的線性相關性關係為：

3.4 n 維向量空間的基變換公式及過渡矩陣

　　若 α₁， α₂， …α₃ 與 β₁， β₂，… β_n是向量空間 V 的兩組基，則基變換公式為：

　　其中 C是可逆矩陣，稱為由基 α1，α2，….αn到基β1，β2，…βn 的過渡矩陣。

　　坐標變換公式：

3.5 向量的內積（點積）

　　點積在數學中，又稱數量積（dot product；scalar product），是指接受在實數R上的兩個向量並返回一個實數值標量的二元運算。它是歐幾里得空間的標準內積。

　　設有 n 維向量：

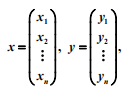
　　則當：

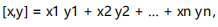
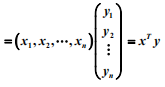
　　此時，我們就把 [x. y] 叫做向量的內積。

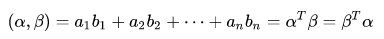
　　內積的性質如下：

3.6 向量的長度

　　幾何空間中向量長度概念的推廣，設 x 為歐式空間 V 的向量，非負實數（x, x）的演算法平方根 √ (x, x) 稱為向量 x 的長度或長，也稱為 x 的模，記為 ||x||。

　　向量的長度具有如下性質：

1，對於任意的 x 屬於 V，|x| >=0， |x|=0 當且僅當 x=0
2，對於任意的 k 屬於 R，x屬於V，|kx|=|k||x|，其中 |k| 是 k的絕對值。

　　老師的PPT如下：

3.7 向量的正交

　　兩兩正交的非零向量組成為正交向量組。若 a₁, a₂,….a_r 是兩兩正交的非零向量，則 a₁, a₂,….a_r 線性無關。

　　例如，已知三維向量空間 R³ 中兩個向量a₁, a₂正交，試求一個非零向量 a₃，使得a₁, a_{2 ，}a_₃ 兩兩正交：

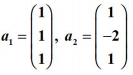
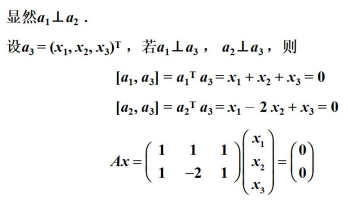
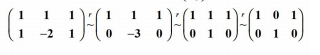
3.8 正交基及規範正交基

　　向量空間一組基中的向量如果兩兩正交，就稱為正交基；若正交基中每個向量都是單位向量，就稱其為規範正交基。

　　其性質如下：

4，線性方程組

4.1 克萊姆法則

　　對於線性方程組：

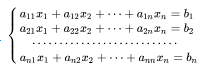
　　如果係數行列式 D = |A| ≠ 0，則方程有唯一解，

　　其中 Dj 是把 D 中第 j 列元素換成方程組右端的常數類所得的行列式。

　　n階矩陣 A 可逆 r(Am*n) = m 只有零解 <==> 對於任意b，Ax = b 總有唯一解，一般地，r(Am*n) <==> Ax=0 只有零解。

4.2 非齊次線性方程組有解的充分必要條件，線性方程組解的性質和解決的結構

4.3 齊次線性方程的基礎解析和通解，解空間，非其次線性方程組的通解

參考鏈接：//zhuanlan.zhihu.com/p/36584206

Tags: 人工智慧必備數學基礎