論文閱讀LR LIO-SAM

2020 年 12 月 28 日
筆記
Paper Reading

Abstract

緊耦合lidar inertial里程計, 用smoothing和mapping.

1. Introduction

緊耦合lidar-inertial里程計.

緊耦合的lidar inertial里程計框架

一般都是用ICP或者是GICP.

在LOAM[1], IMU被引入來de-skew lidar scan, 然後給移動一個先驗做scan-匹配.

在[15], 預積分IMU測量被用來 de-skew 點雲.

一個robocentric lidar-inertial 狀態估計器, R-LINS[16] , 用error-state KF.

LIOM只能 0.6 倍實時

3. LiDAR Inertial Odometry via SAM

A. System Overview

狀態是:

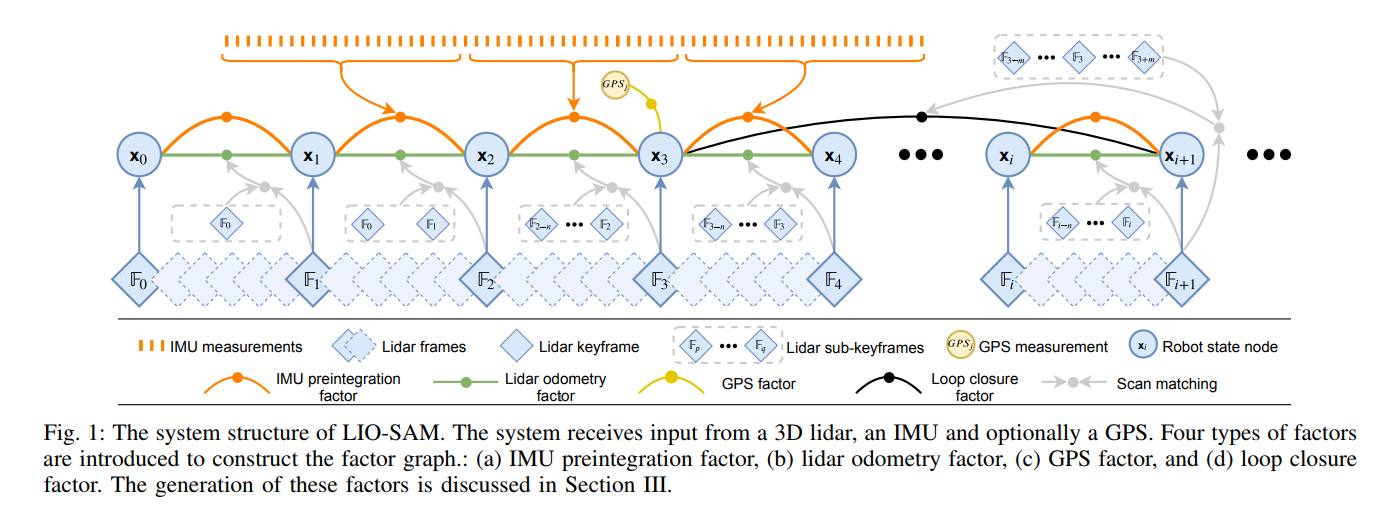
\[\mathbf{x}=\left[\mathbf{R}^{\mathbf{T}}, \mathbf{p}^{\mathbf{T}}, \mathbf{v}^{\mathbf{T}}, \mathbf{b}^{\mathbf{T}}\right]^{\mathbf{T}}
\]

B. IMU Preintegration Factor

角速度, 加速度的測量:

\[\begin{array}{l}
\hat{\boldsymbol{\omega}}_{t}=\boldsymbol{\omega}_{t}+\mathbf{b}_{t}^{\boldsymbol{\omega}}+\mathbf{n}_{t}^{\boldsymbol{\omega}} \\
\hat{\mathbf{a}}_{t}=\mathbf{R}_{t}^{\mathbf{B W}}\left(\mathbf{a}_{t}-\mathbf{g}\right)+\mathbf{b}_{t}^{\mathbf{a}}+\mathbf{n}_{t}^{\mathbf{a}},
\end{array}
\]

這裡 \(\hat{\omega}_t\) 和 \(\hat{a}_t\) 是 raw 測量在 \(B\) 系.

速度, 位置和旋轉在 \(t+\Delta t\)時刻如下:

\[\begin{aligned}
\mathbf{v}_{t+\Delta t}=\mathbf{v}_{t}+\mathbf{g} \Delta t+\mathbf{R}_{t}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{t}^{\mathbf{a}}-\mathbf{n}_{t}^{\mathbf{a}}\right) \Delta t \\
\mathbf{p}_{t+\Delta t}=\mathbf{p}_{t}+\mathbf{v}_{t} \Delta t+\frac{1}{2} \mathbf{g} \Delta t^{2} \\
&+\frac{1}{2} \mathbf{R}_{t}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{t}^{\mathbf{a}}-\mathbf{n}_{t}^{\mathbf{a}}\right) \Delta t^{2} \\
\mathbf{R}_{t+\Delta t}=\mathbf{R}_{t} \exp \left(\left(\hat{\boldsymbol{\omega}}_{t}-\mathbf{b}_{t}^{\omega}-\mathbf{n}_{t}^{\omega}\right) \Delta t\right)
\end{aligned}
\]

這裡 \(R_t = R_t^{WB} = R_t^{{BW}^T}\). 這裡我們假設角速度和加速度的\(B\) 保持不變.

C. LiDAR Odometry Factor

當一個新的scan到達時, 我們先做特徵提取. Edge / planar 特徵被提取來估計局部點的roughness. 有大的 roughness值的實被分類為edge, 值小的就是planar特徵.

1. Sub-keyframes for voxel map

2. Scan-matching

3. Relative transform

edge點和平面點對應如下:

\[\begin{array}{r}
\mathbf{d}_{e_{k}}=\frac{\left|\left(\mathbf{p}_{i+1, k}^{e}-\mathbf{p}_{i, u}^{e}\right) \times\left(\mathbf{p}_{i+1, k}^{e}-\mathbf{p}_{i, v}^{e}\right)\right|}{\left|\mathbf{p}_{i, u}^{e}-\mathbf{p}_{i, v}^{e}\right|} \\
\mathbf{d}_{p_{k}}=\frac{\left(\mathbf{p}_{i, u}^{p}-\mathbf{p}_{i, v}^{p}\right) \times\left(\mathbf{p}_{i, u}^{p}-\mathbf{p}_{i, w}^{p}\right) \mid}{\left|\left(\mathbf{p}_{i, u}^{p}-\mathbf{p}_{i, v}^{p}\right) \times\left(\mathbf{p}_{i, u}^{p}-\mathbf{p}_{i, w}^{p}\right)\right|}
\end{array}
\]

D. GPS Factor

當收到GPS測量的時候, 我會先轉換到局部笛卡爾坐標系.

一般我們只有在估計的位置協方差大於接受的GPS位置協方差的時候才加入 GPS factor.

E. Loop Closure Factor

…

4. Experiments

我們比較了LIO-SAM, LOAM和LIOM. LIO-SAM和LOAM是專註在實時的輸出, 而LIOM是有無限的時間處理的.

A. Rotation Dataset

遇到的最大的旋轉速度是 133.7°/s.

B. Walking Dataset

LIOM只跑了0.56x的實時.

C. Campus Dataset

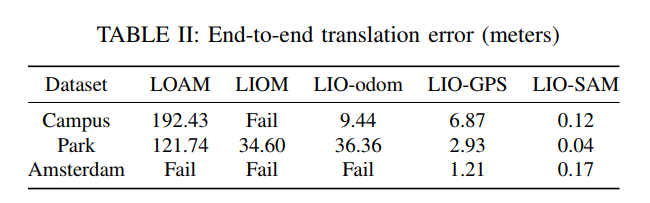
D. Park Dataset

…

E. Amsterdam Dataset

….

F. Benchmarking Results

…

5. Conclusions and Discussion

沒啥.

Tags: Paper Reading