C#數據結構-赫夫曼樹
什麼是赫夫曼樹?
赫夫曼樹(Huffman Tree)是指給定N個權值作為N個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小。哈夫曼樹(也稱為最優二叉樹)是帶權路徑長度最短的樹,權值較大的結點離根較近。
1 public class HNode<T> 2 { 3 public HNode() 4 { 5 data = default(T); 6 weight = 0; 7 leftNode = null; 8 rightNode = null; 9 } 10 11 public HNode(T val) 12 { 13 data = val; 14 weight = 0; 15 leftNode = null; 16 rightNode = null; 17 } 18 19 /// <summary> 20 /// 權重 21 /// </summary> 22 public int weight { get; set; } 23 24 /// <summary> 25 /// 內容 26 /// </summary> 27 public T data { get; set; } 28 29 /// <summary> 30 /// 左樹 31 /// </summary> 32 public HNode<T> leftNode { get; set; } 33 34 /// <summary> 35 /// 右樹 36 /// </summary> 37 public HNode<T> rightNode { get; set; } 38 }
1 /// <summary> 2 /// 赫夫曼樹 3 /// </summary> 4 /// <typeparam name="T"></typeparam> 5 public class HTree<T> 6 { 7 /// <summary> 8 /// 樹的頭結點 9 /// </summary> 10 public HNode<T> head { get; set; } 11 12 /// <summary> 13 /// 構造函數 14 /// </summary> 15 /// <param name="val"></param> 16 public HTree(T val) 17 { 18 head = new HNode<T>(val); 19 } 20 21 public HTree() 22 { 23 head = new HNode<T>(); 24 } 25 /// <summary> 26 /// 構建樹結構 27 /// </summary> 28 /// <param name="list"></param> 29 public void build(List<T> list) 30 { 31 //判斷是否能構建樹結構 32 if (list == null || list.Count <2) 33 throw new ArgumentOutOfRangeException("params error"); 34 //分組統計 35 List<HNode<T>> nodes = new List<HNode<T>>(); 36 nodes.AddRange(from m in list group m by m into g 37 select new HNode<T> { data = g.Key,weight = g.Count()}); 38 //排序 39 nodes = nodes.OrderBy(i => i.weight).ToList(); 40 41 for (int i =1; i< nodes.Count; i++) 42 { 43 HNode<T> parentNode = new HNode<T>(); 44 if (i == 1) 45 { 46 //先取最小的兩個節點 47 parentNode.leftNode = nodes[0]; 48 parentNode.rightNode = nodes[1]; 49 parentNode.weight = nodes[0].weight + nodes[1].weight; 50 } 51 else 52 { 53 //依次取節點構建樹 54 if (head.weight >= nodes[i].weight) 55 { 56 parentNode.leftNode = head; 57 parentNode.rightNode = nodes[i]; 58 } 59 else 60 { 61 parentNode.rightNode = head; 62 parentNode.leftNode = nodes[i]; 63 } 64 parentNode.weight = head.weight + nodes[i].weight; 65 } 66 head = parentNode; 67 } 68 } 69 70 /// <summary> 71 /// 先序遍歷 72 /// </summary> 73 /// <param name="index"></param> 74 public void PreorderTraversal(HNode<T> node) 75 { 76 //遞歸的終止條件 77 if (head == null) 78 { 79 Console.WriteLine("當前樹為空"); 80 return; 81 } 82 if (node != null) 83 { 84 if(node.data != null) 85 Console.WriteLine($"{node.data} {node.weight}"); 86 PreorderTraversal(node.leftNode); 87 PreorderTraversal(node.rightNode); 88 } 89 } 90 }
測試程式碼:
1 List<string> list = new List<string>() { "A","B", "B", "C", "C", "C", "D", "D", "D", "D", "E", "E", "E", "E", "E" }; 2 HTree<string> tree = new HTree<string>(); 3 tree.build(list); 4 tree.PreorderTraversal(tree.head);
列印結果:
A 1 B 2 C 3 D 4 E 5
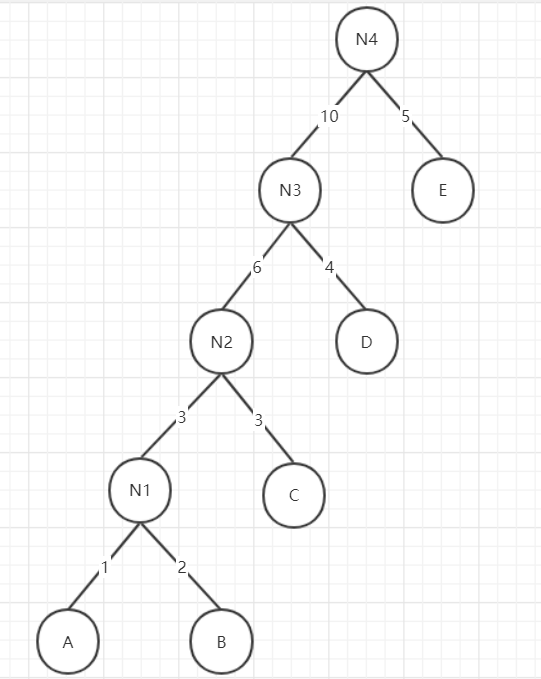
用這個例子現在我們看下構建的二叉樹結構: