JavaScript 數據結構與演算法之美 – 你可能真的不懂遞歸
- 2019 年 10 月 3 日
- 筆記

1. 前言
- 演算法為王。
- 排序演算法博大精深,前輩們用了數年甚至一輩子的心血研究出來的演算法,更值得我們學習與推敲。
因為之後要講有內容和演算法,其程式碼的實現都要用到遞歸,所以,搞懂遞歸非常重要。
2. 定義
- 方法或函數調用自身的方式稱為遞歸調用,調用稱為遞,返回稱為歸。
簡單來說就是:自己調用自己。
現實例子:周末你帶著女朋友去電影院看電影,女朋友問你,咱們現在坐在第幾排啊 ?電影院裡面太黑了,看不清,沒法數,現在你怎麼辦 ?
於是你就問前面一排的人他是第幾排,你想只要在他的數字上加一,就知道自己在哪一排了。
但是,前面的人也看不清啊,所以他也問他前面的人。
就這樣一排一排往前問,直到問到第一排的人,說我在第一排,然後再這樣一排一排再把數字傳回來。
直到你前面的人告訴你他在哪一排,於是你就知道答案了。
基本上,所有的遞歸問題都可以用遞推公式來表示,比如:
f(n) = f(n-1) + 1; // 其中,f(1) = 1 f(n) 表示你想知道自己在哪一排,f(n-1) 表示前面一排所在的排數,f(1) = 1 表示第一排的人知道自己在第一排。
有了這個遞推公式,我們就可以很輕鬆地將它改為遞歸程式碼,如下:
function f(n) { if (n == 1) return 1; return f(n-1) + 1; }3. 為什麼使用遞歸 ?遞歸的優缺點 ?
- 優點:程式碼的表達力很強,寫起來簡潔。
- 缺點:空間複雜度高、有堆棧溢出風險、存在重複計算、過多的函數調用會耗時較多等問題。
4. 什麼樣的問題可以用遞歸解決呢 ?
一個問題只要同時滿足以下 3 個條件,就可以用遞歸來解決。
- 問題的解可以分解為幾個子問題的解。何為子問題 ?就是數據規模更小的問題。
比如,前面講的電影院的例子,你要知道,自己在哪一排的問題,可以分解為前一排的人在哪一排這樣一個子問題。 - 問題與子問題,除了數據規模不同,求解思路完全一樣
比如電影院那個例子,你求解自己在哪一排的思路,和前面一排人求解自己在哪一排的思路,是一模一樣的。 - 存在遞歸終止條件
比如電影院的例子,第一排的人不需要再繼續詢問任何人,就知道自己在哪一排,也就是 f(1) = 1,這就是遞歸的終止條件。
5. 遞歸常見問題及解決方案
- 警惕堆棧溢出:可以聲明一個全局變數來控制遞歸的深度,從而避免堆棧溢出。
- 警惕重複計算:通過某種數據結構來保存已經求解過的值,從而避免重複計算。
6. 如何實現遞歸 ?
1. 遞歸程式碼編寫
寫遞歸程式碼的關鍵就是找到如何將大問題分解為小問題的規律,並且基於此寫出遞推公式,然後再推敲終止條件,最後將遞推公式和終止條件翻譯成程式碼。
2. 遞歸程式碼理解
對於遞歸程式碼,若試圖想清楚整個遞和歸的過程,實際上是進入了一個思維誤區。
那該如何理解遞歸程式碼呢 ?
- 如果一個問題 A 可以分解為若干個子問題 B、C、D,你可以假設子問題 B、C、D 已經解決。
- 而且,你只需要思考問題 A 與子問題 B、C、D 兩層之間的關係即可,不需要一層層往下思考子問題與子子問題,子子問題與子子子問題之間的關係。
- 屏蔽掉遞歸細節,這樣子理解起來就簡單多了。
因此,理解遞歸程式碼,就把它抽象成一個遞推公式,不用想一層層的調用關係,不要試圖用人腦去分解遞歸的每個步驟。
7. 例子
1. 一個階乘的例子:
function fact(num) { if (num <= 1) { return 1; } else { return num * fact(num - 1); } } fact(3) // 結果為 6以下程式碼可導致出錯:
var anotherFact = fact; fact = null; alert(antherFact(4)); //出錯 由於 fact 已經不是函數了,所以出錯。
使用 arguments.callee
arguments.callee 是一個指向正在執行的函數的指針,arguments.callee 返回正在被執行的對現象。
新的函數為:
function fact(num){ if (num <= 1){ return 1; }else{ return num * arguments.callee(num - 1); //此處更改了。 } } var anotherFact = fact; fact = null; alert(antherFact(4)); // 結果為 242. 再看一個多叉樹的例子
先看圖
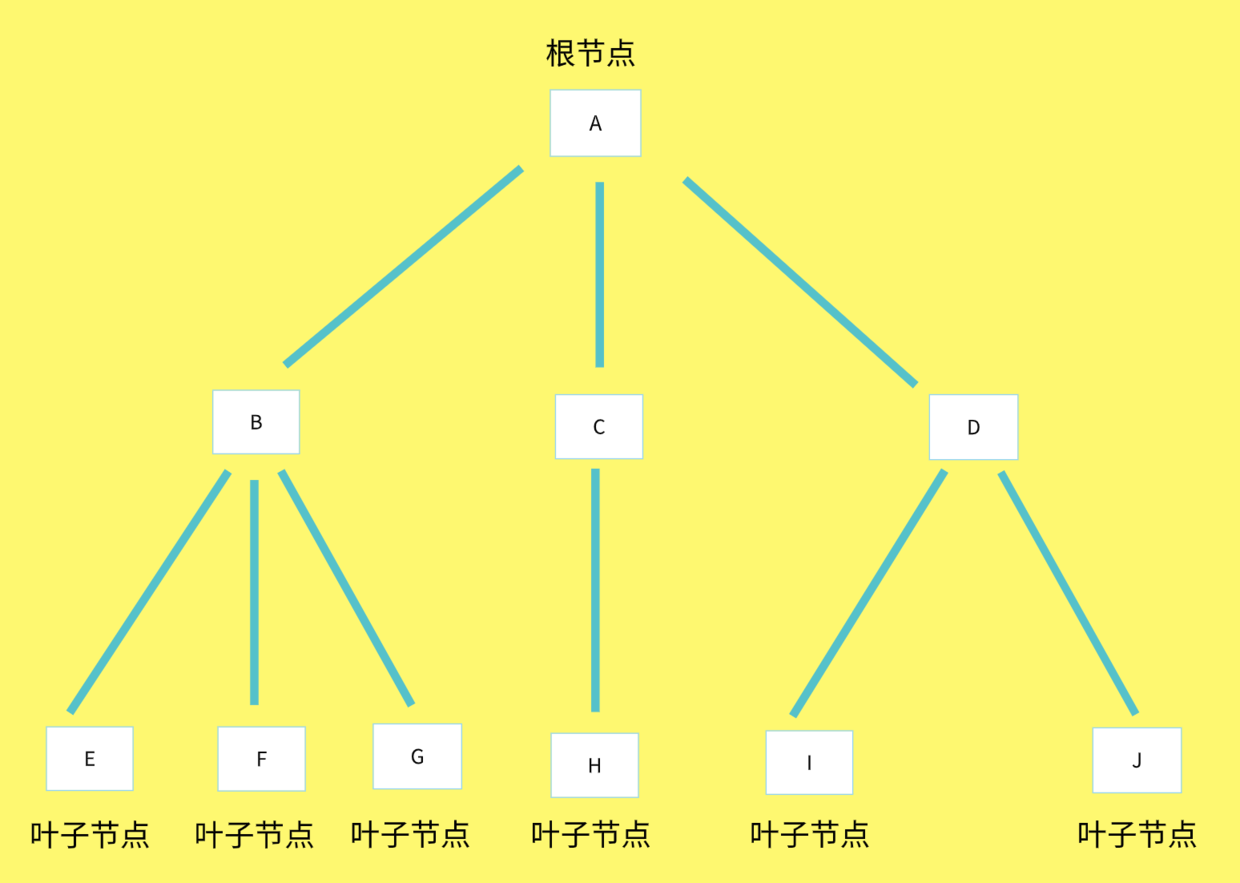
葉子結點:就是深度為 0 的結點,也就是沒有孩子結點的結點,簡單的說就是一個二叉樹任意一個分支上的終端節點。
數據結構格式,參考如下程式碼:
const json = { name: 'A', children: [ { name: 'B', children: [ { name: 'E', }, { name: 'F', }, { name: 'G', } ] }, { name: 'C', children: [ { name: 'H' } ] }, { name: 'D', children: [ { name: 'I', }, { name: 'J', } ] } ] }我們如何獲取根節點的所有葉子節點個數呢 ?
遞歸程式碼如下:
/** * 獲取根節點的所有 葉子節點 個數 * @param {Object} json Object 對象 */ function getLeafCountTree(json) { if(!json.children){ return 1; } else { let leafCount = 0; for(let i = 0 ; i < json.children.length ; i++){ // leafCount = leafCount + getLeafCountTree(json.children[i]); leafCount = leafCount + arguments.callee(json.children[i]); } return leafCount; } }遞歸遍歷是比較常用的方法,比如:省市區遍歷成樹、多叉樹、階乘等。
8. 最後
如果覺得本文還不錯,記得給個 star , 你的 star 是我持續更新的動力!。
筆者 GitHub。
參考文章:
