EM 演算法-對鳶尾花數據進行聚類

公號：碼農充電站pro
主頁：//codeshellme.github.io

之前介紹過K 均值演算法，它是一種聚類演算法。今天介紹EM 演算法，它也是聚類演算法，但比K 均值演算法更加靈活強大。

EM 的全稱為 Expectation Maximization，中文為期望最大化演算法，它是一個不斷觀察和調整的過程。

1，和面過程

在這裡插入圖片描述

我們先來看一下和面的過程。

通常情況下，如果你事先不知道面與水的比例，和面過程可能是下面這樣：

  1. 先放入一些面和水。
  2. 將麵糰揉拌均勻。
  3. 觀察麵糰的稀稠程度：如果麵糰比較稀，則加入少許面；如果麵糰比較稠，則加入少許水。
  4. 如此往複第2，3步驟，直到麵糰的稀稠程度達到預期。

這個和面過程，就是一個EM 過程：

  • 先加入一些面和水，將麵糰揉拌均勻，並觀察麵糰的稀稠程度。這是E 過程。
  • 不斷的加入水和面（調整水和面的比例），直到達到預期麵糰程度。這是M 過程。

2，再看K 均值演算法

在介紹K 均值 聚類演算法時，展示過一個給二維坐標點進行聚類的例子。

我們再來看一下這個例子，如下圖：

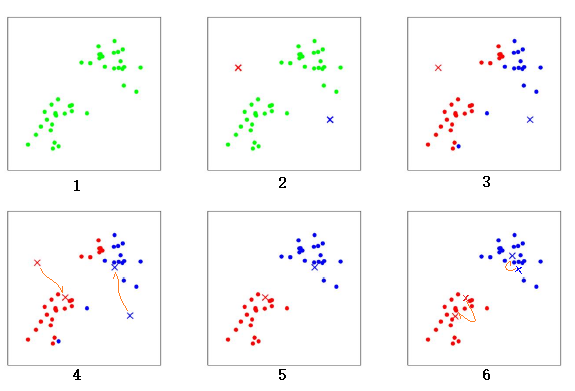
在這裡插入圖片描述

上圖是一個聚類的過程，共有6 個步驟：

  1. 初始時散點（綠色點）的分布。
  2. 隨機選出兩個中心點的位置，紅色x 和藍色x。
  3. 計算所有散點分別到紅色x 和藍色x的距離，距離紅色x 近的點標紅色，距離藍色x近的點標藍色。
  4. 重新計算兩個中心點的位置，兩個中心點分別移動到新的位置。
  5. 重新計算所有散點分別到紅色x 和藍色x的距離，距離紅色x 近的點標紅色，距離藍色x近的點標藍色。
  6. 再次計算兩個中心點的位置，兩個中心點分別移動到新的位置。中心點的位置幾乎不再變化，聚類結束。

經過以上步驟就完成了一個聚類過程。

實際上，K 均值演算法也是一個EM 過程：

  • 確定當前各類中心點的位置，並計算各個散點到現有的中心點的距離。這是E 過程。
  • 將各個散點歸屬到各個類中，重新計算各個類的中心點，直到各類的中心點不再改變。這是M 過程。

3，EM 演算法

將二維數據點的聚類過程，擴展為一般性的聚類問題，EM 演算法是這樣一個模型：對於待分類的數據點，EM 演算法讓電腦通過一個不斷迭代的過程，來構建一個分類模型。

EM 演算法分為兩個過程：

  • E 過程：根據現有的模型，計算各個數據輸入到模型中的計算結果，這稱為期望值計算過程，即 E 過程。
  • M 過程：重新計算模型參數，以最大化期望值，這稱為最大化過程，即M 過程。

以二維數據點的聚類過程為例，我們定義：

  • 同一類中各個點到該類中心的平均距離為 d；
  • 不同類之間的平均距離為 D。

那麼二維數據點聚類的M 過程，就是尋求最大化的D 和 -d。我們希望的聚類結果是，同一類的點距離較近，不同類之間距離較遠。

EM 演算法不是單個演算法，而是一類演算法。只要滿足EM 這兩個過程的演算法都可以被稱為EM 演算法。常見的EM 演算法有GMM 高斯混合模型和HMM 隱馬爾科夫模型。

4，最大似然估計

在這裡插入圖片描述

高等數學中有一門課叫做《概率論與數理統計》，其中講到了參數估計。

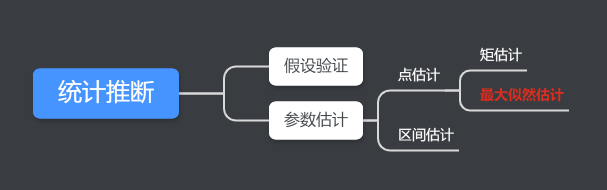
統計推斷是數理統計的重要組成部分，它是指利用來自總體的樣本提供的資訊，對總體的某些特徵進行估計或推斷，從而認識整體。

統計推斷分為兩大類：參數估計和假設檢驗。

我們假設，對於某個數據集，其分布函數的基本形式已知，但其中含有一個或多個未知參數。

參數估計就是討論如何根據來自總體的樣本提供的資訊對未知參數做出估計。參數估計包括點估計和區間估計。其中，點估計中有兩種方法：矩估計法和最大似然估計法。

最大似然估計是一種通過已知結果，估計未知參數的方法。

在這裡插入圖片描述

5，EM 演算法原理

EM 演算法使用的是最大似然估計的原理，它通過觀察樣本，來找出樣本的模型參數。

下面通過一個投硬幣的例子，來看下EM 演算法的計算過程。

這個例子來自《Nature》（自然）期刊的論文《What is the expectation maximization algorithm？》（什麼是期望最大化演算法？）。

假定有兩枚不同的硬幣 A 和 B，它們的重量分布 θA​ 和 θB​ 是未知的，則可以通過拋擲硬幣，計算正反面各自出現的次數來估計θA​ 和 θB​。

方法是在每一輪中隨機抽出一枚硬幣拋擲 10 次，同樣的過程執行 5 輪，根據這 50 次投幣的結果來計算 θA​ 和 θB​​ 的最大似然估計。

投擲硬幣的過程，記錄如下：

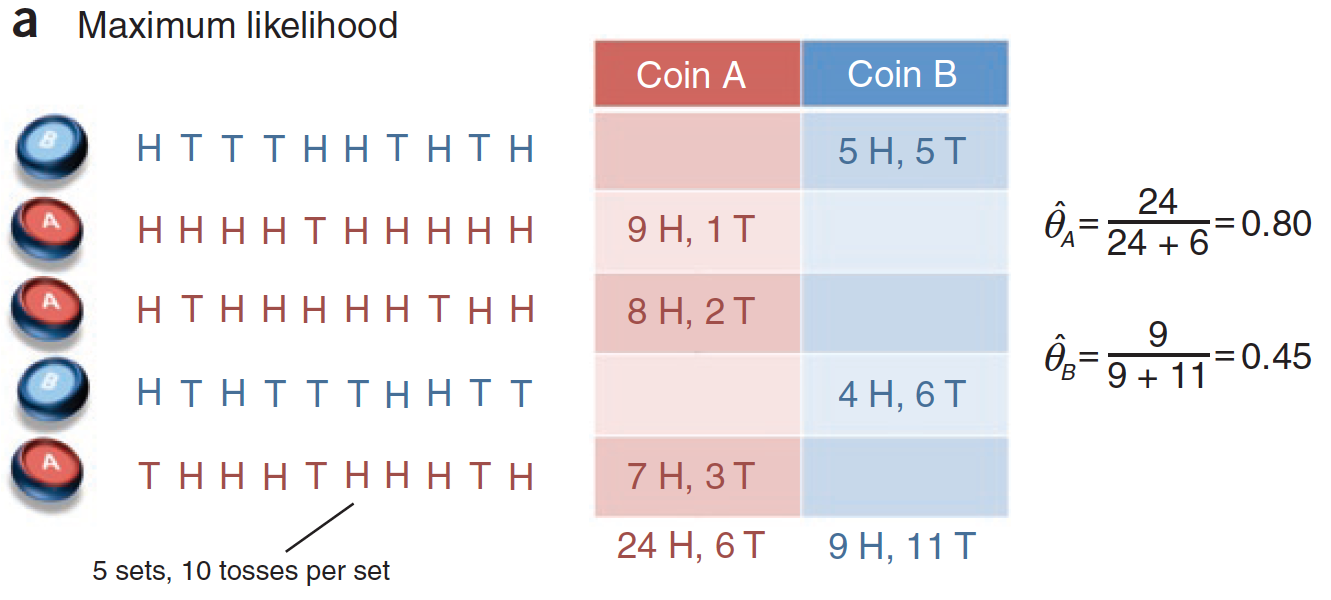
在這裡插入圖片描述

第1 到5 次分別投擲的硬幣是 B，A，A，B，A。H 代表正面，T 代表負面。將上圖轉化為表格，如下：

次數 硬幣 正面數 負面數
1 B 5 5
2 A 9 1
3 A 8 2
4 B 4 6
5 A 7 3

通過這個表格，可以直接計算 θA​ 和 θB​​，如下：

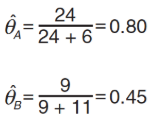
在這裡插入圖片描述

顯然，如果知道每次投擲的硬幣是A 還是B，那麼計算θA​ 和 θB 是非常簡單的。

但是，如果不知道每次投擲的硬幣是A 還是B，該如何計算θA​ 和 θB 呢？

此時我們將上面表格中的硬幣一列隱藏起來，這時硬幣就是隱變數。所以我們只知道如下數據：

次數 正面數 負面數
1 5 5
2 9 1
3 8 2
4 4 6
5 7 3

這時想要計算 θA​ 和 θB，就要用最大似然估計的原理。

計算過程如下圖：

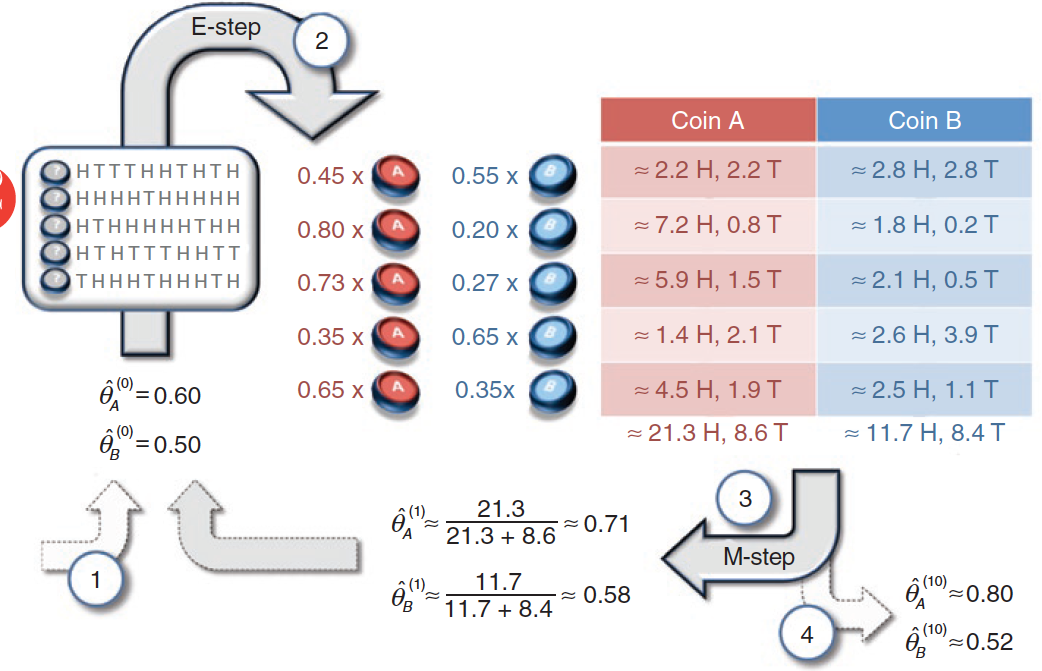
在這裡插入圖片描述

第一步

先為 θA​ 和 θB 設定一個初始值，比如 θA = 0.6，θB = 0.5。

第二步

我們知道每一輪投幣的正 / 負面的次數：

  • 第1輪：5 正 5 負，計算出現這種結果的概率：
    • 如果是A 硬幣，那麼P(H5T5|A) = 0.6^5 * 0.4^5
    • 如果是B 硬幣，那麼P(H5T5|B) = 0.5^5 * 0.5^5
    • 將 P(H5T5|A) 和 P(H5T5|B) 歸一化處理，可得：
    • P(H5T5|A) = 0.45，P(H5T5|B) = 0.55
  • 第2輪：9 正 1 負，計算出現這種結果的概率：
    • 如果是A 硬幣，那麼P(H9T1|A) = 0.6^9 * 0.4^1
    • 如果是B 硬幣，那麼P(H9T1|B) = 0.5^9 * 0.5^1
    • 將 P(H9T1|A) 和 P(H9T1|B) 歸一化處理，可得：
    • P(H9T1|A) = 0.8，P(H9T1|B) = 0.2
  • 第3輪：8 正 2 負，計算出現這種結果的概率：
    • 如果是A 硬幣，那麼P(H8T2|A) = 0.6^8 * 0.4^2
    • 如果是B 硬幣，那麼P(H8T2|B) = 0.5^8 * 0.5^2
    • 將 P(H8T2|A) 和 P(H8T2|B) 歸一化處理，可得：
    • P(H8T2|A) = 0.73，P(H8T2|B) = 0.27
  • 第4輪：4 正 6 負，計算出現這種結果的概率：
    • 如果是A 硬幣，那麼P(H4T6|A) = 0.6^4 * 0.4^6
    • 如果是B 硬幣，那麼P(H4T6|B) = 0.5^4 * 0.5^6
    • 將 P(H4T6|A) 和 P(H4T6|B) 歸一化處理，可得：
    • P(H4T6|A) = 0.35，P(H4T6|B) = 0.65
  • 第5輪：7 正 3 負，計算出現這種結果的概率：
    • 如果是A 硬幣，那麼P(H7T3|A) = 0.6^7 * 0.4^3
    • 如果是B 硬幣，那麼P(H7T3|B) = 0.5^7 * 0.5^3
    • 將 P(H7T3|A) 和 P(H7T3|B) 歸一化處理，可得：
    • P(H7T3|A) = 0.65，P(H7T3|B) = 0.35

然後，根據每一輪的 P(HmTn|A) 和 P(HmTn|B)，可以計算出每一輪的正 / 負面次數。

m 為正面次數，n 為負面次數。

對於硬幣A，結果如下：

輪數 P(HmTn|A) m n 正面數 負面數
1 0.45 5 5 0.45*5=2.2 0.45*5=2.2
2 0.8 9 1 0.8*9=7.2 0.8*1=0.8
3 0.73 8 2 0.73*8=5.9 0.73*2=1.5
4 0.35 4 6 0.35*4=1.4 0.35*6=2.1
5 0.65 7 3 0.65*7=4.5 0.65*3=1.9
總計 – – – 21.3 8.6

對於硬幣B，結果如下：

輪數 P(HmTn|B) m n 正面數 負面數
1 0.55 5 5 0.55*5=2.8 0.55*5=2.8
2 0.2 9 1 0.2*9=1.8 0.2*1=0.2
3 0.27 8 2 0.27*8=2.1 0.27*2=0.5
4 0.65 4 6 0.65*4=2.6 0.65*6=3.9
5 0.35 7 3 0.35*7=2.5 0.35*3=1.1
總計 – – – 11.7 8.4

第三步

根據上面兩個表格，可以得出（第1次迭代的結果） θA 和 θB：

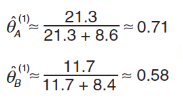
在這裡插入圖片描述

根據這個估計值，再次回到第一步去計算。

如此往複第一、二、三步，經過10次迭代之後，θA 和 θB 的估計值為：

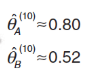
在這裡插入圖片描述

最終，θA 和 θB 將收斂到一個幾乎不變的值，此時迭代結束。這樣我們就求解出了θA 和 θB 的最大似然估計值。

我們將上述過程中，第一步稱為初始化參數，第二步稱為觀察預期，第三步稱為重新估計參數。

第一、二步為E 過程，第三步為M 過程，這就是EM 演算法的過程。

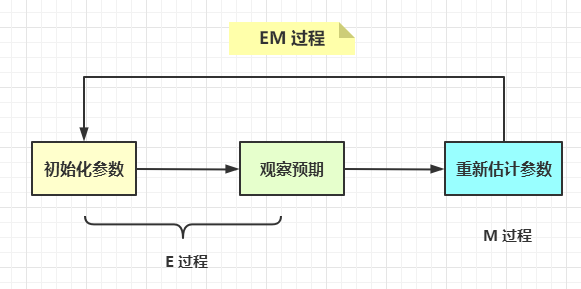
在這裡插入圖片描述

如果我們有一個待聚類的數據集，我們把潛在的類別當做隱變數，樣本當做觀察值，這樣就可以把聚類問題轉化成參數估計問題。這就是EM 聚類的原理。

6，硬聚類與軟聚類

與 K 均值演算法相比，K 均值演算法是通過距離來區分樣本之間的差別，且每個樣本在計算的時候只能屬於一個分類，我們稱之為硬聚類演算法。

而 EM 聚類在求解的過程中，實際上每個樣本都有一定的概率和每個聚類相關，這叫做軟聚類演算法。

7，EM 聚類的缺點

EM 聚類演算法存在兩個比較明顯的問題。

第一個問題是，EM 演算法計算複雜，收斂較慢，不太適合大規模數據集和高維數據。

第二個問題是，EM 演算法不一定能給出全局最優解：

  • 當優化的目標函數是凸函數時，一定可以得到全局最優解。
  • 當優化的目標函數不是凸函數時，可能會得到局部最優解，而非全局最優解。

8，GMM 高斯混合模型

上文中介紹過，常見的EM 演算法有GMM 高斯混合模型和HMM 隱馬爾科夫模型。這裡主要介紹GMM 高斯混合模型的實現。

sklearn 庫的mixture 模組中的GaussianMixture 類是GMM 演算法的實現。

先來看下 GaussianMixture 類的原型：

GaussianMixture(
  n_components=1,
  covariance_type='full', 
  tol=0.001, 
  reg_covar=1e-06, 
  max_iter=100, 
  n_init=1, 
  init_params='kmeans', 
  weights_init=None, 
  means_init=None, 
  precisions_init=None, 
  random_state=None, 
  warm_start=False, 
  verbose=0, 
  verbose_interval=10)

這裡介紹幾個重要的參數：

  • n_components：代表高斯混合模型的個數，也就是我們要聚類的個數，默認值為 1。
  • covariance_type：代表協方差類型。一個高斯混合模型的分布是由均值向量和協方差矩陣決定的，所以協方差的類型也代表了不同的高斯混合模型的特徵。協方差類型有 4 種取值：
    • full，代表完全協方差，也就是元素都不為 0；
    • tied，代表相同的完全協方差；
    • diag，代表對角協方差，也就是對角不為 0，其餘為 0；
    • spherical，代表球面協方差，非對角為 0，對角完全相同，呈現球面的特性。
  • max_iter：代表最大迭代次數，默認值為 100。

9，對鳶尾花數據集聚類

在《決策樹演算法-實戰篇-鳶尾花及波士頓房價預測》中我們介紹過鳶尾花數據集。這裡我們使用GMM 演算法對該數據進行聚類。

首先載入數據集：

from sklearn.datasets import load_iris

iris = load_iris()   	# 載入數據集
features = iris.data	# 獲取特徵集
labels = iris.target    # 獲取目標集

在聚類演算法中，只需要特徵數據 features，而不需要目標數據labels，但可以使用 labels 對聚類的結果做驗證。

構造GMM聚類：

from sklearn.mixture import GaussianMixture

# 原數據中有 3 個分類，所以這裡我們將 n_components 設置為 3
gmm = GaussianMixture(n_components=3, covariance_type='full')

對數據集進行聚類：

prediction_labels = gmm.fit_predict(features)

查看原始分類：

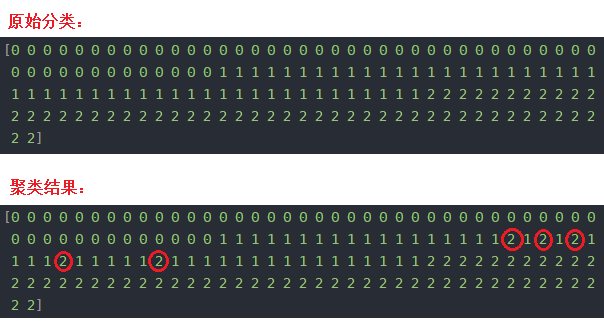
>>> print(labels)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2]

查看聚類結果：

>>> print(prediction_labels)
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 2 1 2 1
 1 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 
 2 2]

對比原始分類和聚類結果，聚類結果中只有個別數據分類錯誤，我用紅圈標了出來：

在這裡插入圖片描述

10，評估聚類結果

我們可以使用 Calinski-Harabaz 指標對聚類結果進行評估。

sklearn 庫實現了該指標的計算，即 calinski_harabasz_score 方法，該方法會計算出一個分值，分數越高，代表聚類效果越好，也就是相同類中的差異性小，不同類之間的差異性大。

下面對鳶尾花數據集的聚類結果進行評估，傳入特徵數據和聚類結果：

>>> from sklearn.metrics import calinski_harabasz_score
>>> calinski_harabasz_score(features, prediction_labels)
481.78070899745234

我們也可以傳入特徵數據和原始結果：

>>> calinski_harabasz_score(features, labels)
487.33087637489984

可以看到，對於原始結果計算出的分值是487.33，對於預測結果計算出的分值是481.78，相差並不多，說明預測結果還是不錯。

一般情況下，一個需要聚類的數據集並沒有目標數據，所以只能對預測結果進行評分。我們需要人工對聚類的含義結果進行分析。

11，總結

本篇文章主要介紹了如下內容：

  • EM 演算法的過程及原理，介紹了一個投擲硬幣的例子。
  • 硬聚類與軟聚類的區別。
  • EM 聚類的缺點：
    • 計算複雜度較大。
    • 有可能得不到全局最優解。
  • 使用GMM 演算法對鳶尾花數據進行聚類。
  • 使用 Calinski-Harabaz 指標對聚類結果進行評估。

（本節完。）

推薦閱讀：

K 均值演算法-如何讓數據自動分組

Apriori 演算法-如何進行關聯規則挖掘

PageRank 演算法-Google 如何給網頁排名

數據變換-歸一化與標準化

如何使用Python 進行數據可視化

歡迎關注作者公眾號，獲取更多技術乾貨。

碼農充電站pro

Tags:

VirMach 便宜 VPS

QNews

QNews