堆的原理和實現
- 2019 年 10 月 3 日
- 筆記
一、前言
本文將詳細為大家講解關於堆這種數據結構。學了本章以後我們會發現,呃呵,原來…名字聽起來高大上的數據結構也就那麼回事。
後面會持續更新數據結構相關的博文。
數據結構專欄:https://www.cnblogs.com/hello-shf/category/1519192.html
git傳送門:https://github.com/hello-shf/data-structure.git
二、堆
堆這種數據結構,有很多的實現,比如:最大堆,最小堆,斐波那鍥堆,左派堆,斜堆等。從孩子節點的個數上還可以分為二叉堆,N叉堆等。本文我們從最大二叉堆堆入手看看堆究竟是什麼高大上的東東。
2.1、什麼是堆
我們先看看它的定義
1 堆是一種完全二叉樹(不是平衡二叉樹,也不是二分搜索樹哦) 2 堆要求孩子節點要小於等於父親節點(如果是最小堆則大於等於其父親節點)
滿足以上兩點性質即可成為一棵合格的堆數據結構。我們解讀一下上面的兩點性質
1,堆是一種完全二叉樹,關於完全二叉樹,在我另一篇部落格《二分搜索樹》中有詳細的介紹,要注意堆是一種建立在二叉樹上的數據結構,不同於AVL或者紅黑樹是建立在二分搜索樹上的數據結構。
2,堆要求孩子節點要大於等於父親節點,該定義是針對的最大堆。對於最小堆,孩子節點小於或者等於其父親節點。
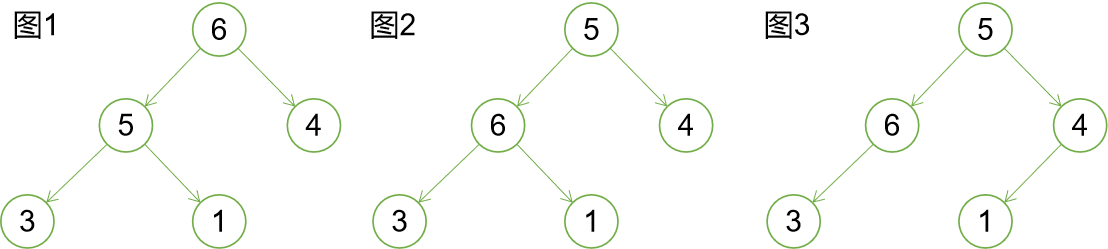
如上所示,只有圖1是合格的最大堆,圖2不滿足父節點大於或者等於孩子節點的性質。圖3不滿足完全二叉樹的性質。
2.2、堆的存儲結構
前面我們說堆是一個完全二叉樹,其中一種在合適不過的存儲方式就是數組。首先從下圖看一下用數組表示堆的可行性。
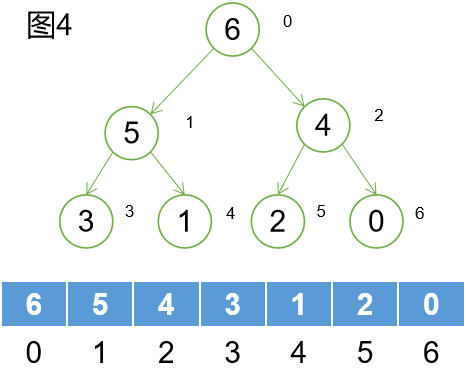
看了上圖,說明數組確實是可以表示一個二叉堆的。使用數組來存儲堆的節點資訊,有一種天然的優勢那就是節省記憶體空間。因為數組佔用的是連續的記憶體空間,相對來說對於散列存儲的結構來說,數組可以節省連續的記憶體空間,不會將記憶體打亂。
接下來看看數組到二叉堆的下標表示。將數組的索引設為 i。則:
左孩子找父節點:parent(i)= (i – 1)/2。比如2元素的索引為5,其父親節點4的下標parent(2)= (5 – 1)/2 = 2;
右孩子找父節點:parent(i)= (i-2)/ 2。比如0元素找父節點 (6-2)/2= 2;
其實可以將上面的兩種方法合併成一個,即parent(i)= (i – 1)/2;從java語法出發大家可以發現,整數相除得到的就是省略了小數位的。所以。。。你懂得。
同理
父節點找左孩子:leftChild(i)= parent(i)* 2 + 1。
父節點找右孩子:rightChild(i) = parent(i)*2 + 2。
三、最大二叉堆的實現
3.1、構建基礎程式碼
上面分析了數組作為堆存儲結構的可行性分析。接下來我們通過數組構建一下堆的基礎結構
1 /** 2 * 描述:最大堆 3 * 4 * @Author shf 5 * @Date 2019/7/29 10:13 6 * @Version V1.0 7 **/ 8 public class MaxHeap<E extends Comparable<E>> { 9 //使用數組存儲 10 private Array<E> data; 11 public MaxHeap(){ 12 data = new Array<>(); 13 } 14 public MaxHeap(int capacity){ 15 data = new Array<>(capacity); 16 } 17 public int size(){ 18 return this.data.getSize(); 19 } 20 public boolean isEmpty(){ 21 return this.data.isEmpty(); 22 } 23 24 /** 25 * 根據當前節點索引 index 計算其父節點的 索引 26 * @param index 27 * @return 28 */ 29 private int parent(int index) { 30 if(index ==0){ 31 throw new IllegalArgumentException("該節點為根節點"); 32 } 33 return (index - 1) / 2;//這裡為什麼不分左右?因為java中 / 運算符只保留整數位。 34 } 35 36 /** 37 * 返回索引為 index 節點的左孩子節點的索引 38 * @param index 39 * @return 40 */ 41 private int leftChild(int index){ 42 return index*2 + 1; 43 } 44 45 /** 46 * 返回索引為 index 節點的右孩子節點的索引 47 * @param index 48 * @return 49 */ 50 private int rightChild(int index){ 51 return index*2 + 2; 52 } 53 }
3.2、插入和上浮 sift up
向堆中插入元素意味著該堆的性質可能遭到破壞,所以這是如同向AVL中插入元素後需要再平衡是一個道理,需要調整堆中元素的位置,使之重新滿足堆的性質。在最大二叉堆中,要堆化一個元素,需要向上查找,找到它的父節點,大於父節點則交換兩個元素,重複該過程直到每個節點都滿足堆的性質為止。這個過程我們稱之為上浮操作。下面我們用圖例描述一下這個過程:

如上圖5所示,我們向該堆中插入一個元素15。在數組中位於數組尾部。
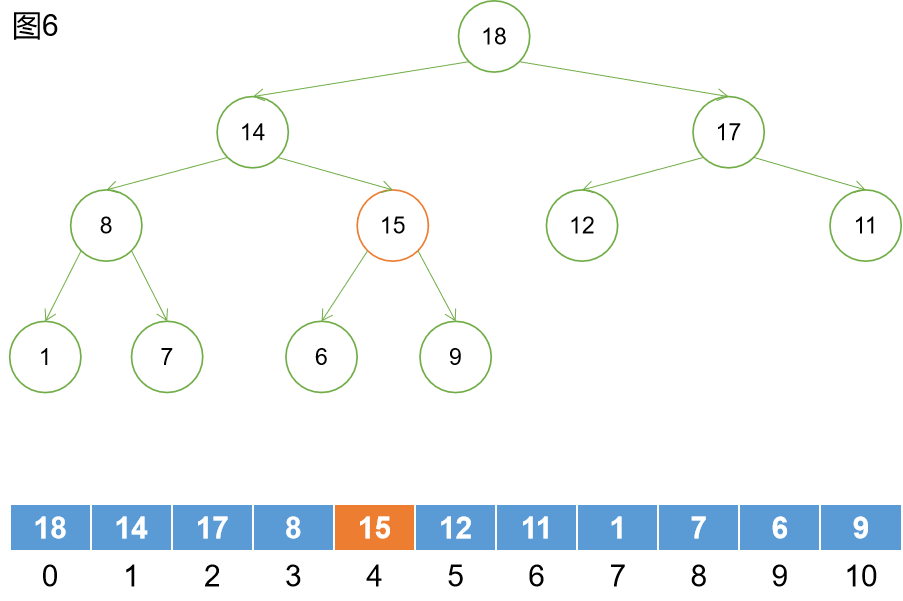
如圖6所示,向上查找,發現15大於它的父節點,所以進行交換。
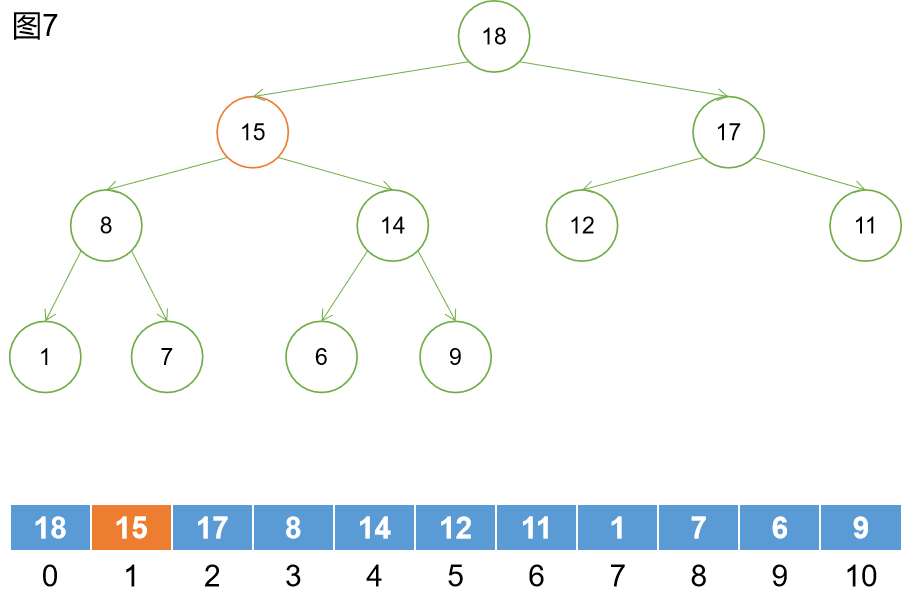
如圖7所示,繼續向上查找,發現仍大於其父節點14。繼續交換。
然後還會繼續向上查找,發現小於其父節點19,停止上浮操作。整個二叉堆通過上浮操作維持了其性質。上浮操作的時間複雜度為O(logn)
插入和上浮操作的程式碼實現很簡單,如下所示。
1 /** 2 * 向堆中添加元素 3 * @param e 4 */ 5 public void add(E e){ 6 // 向數組尾部添加元素 7 this.data.addLast(e); 8 siftUp(data.getSize() - 1); 9 } 10 11 /** 12 * 上浮操作 13 * @param k 14 */ 15 private void siftUp(int k) { 16 // 上浮,如果大於父節點,進行交換 17 while(k > 0 && get(k).compareTo(get(parent(k))) > 0){ 18 data.swap(k, parent(k)); 19 k = parent(k); 20 } 21 }
3.3、取出堆頂元素和下沉 sift down
上面我們介紹了插入和上浮操作,那刪除和下沉操作將不再是什麼難題。一般的如果我們取出堆頂元素,我們選擇將該數組中的最後一個元素替換堆頂元素,返回堆頂元素,刪除最後一個元素。然後再對該元素做下沉操作 sift down。接下來我們通過圖示看看一下過程。
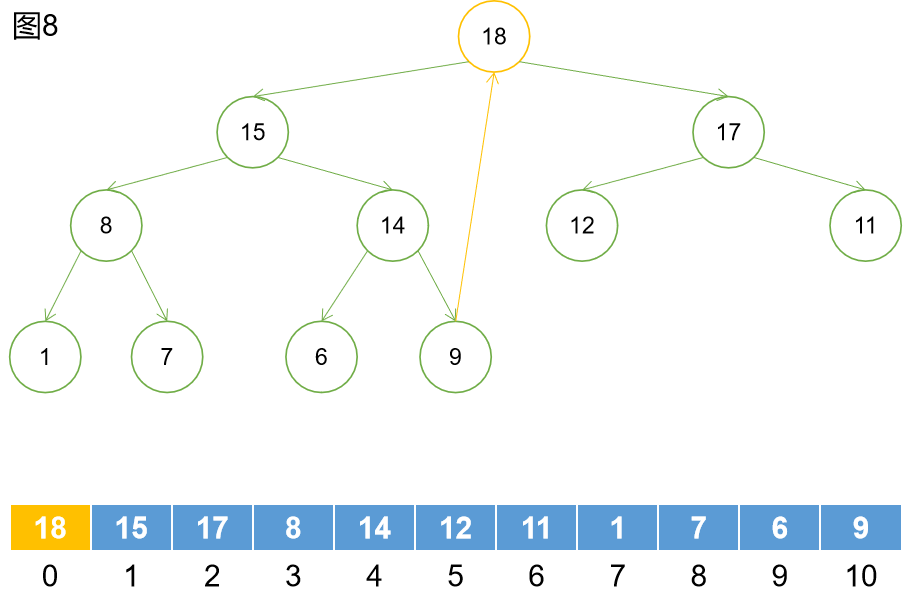
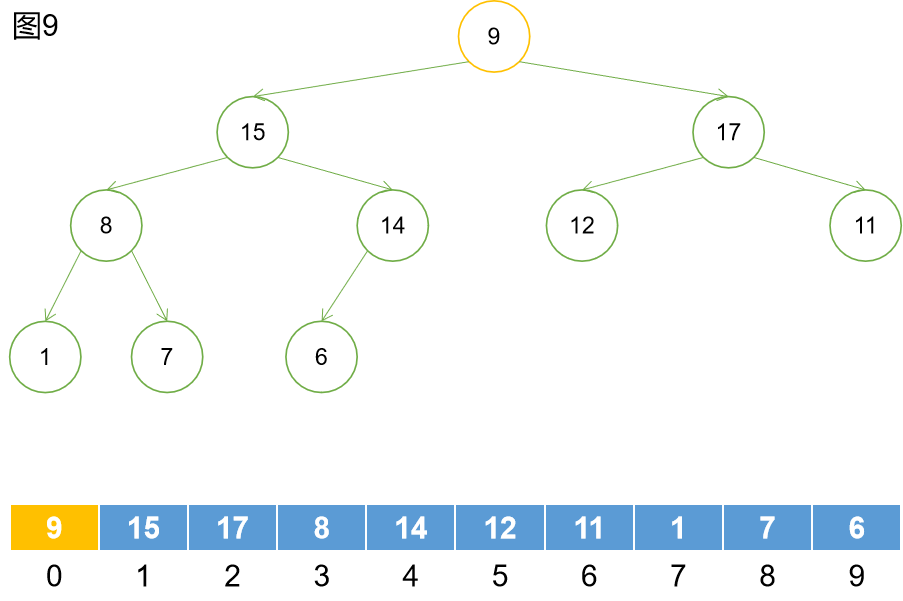
如上圖8所示,將堆頂元素取出,然後讓最後一個元素移動到堆頂位置。刪除最後一個元素,這時得到圖9的結果。

如圖10,堆頂的9元素會分別和其左右孩子節點進行比較,選出較大的孩子節點和其進行交換。很明顯右孩子17大於左孩子15。即和右孩子進行交換。
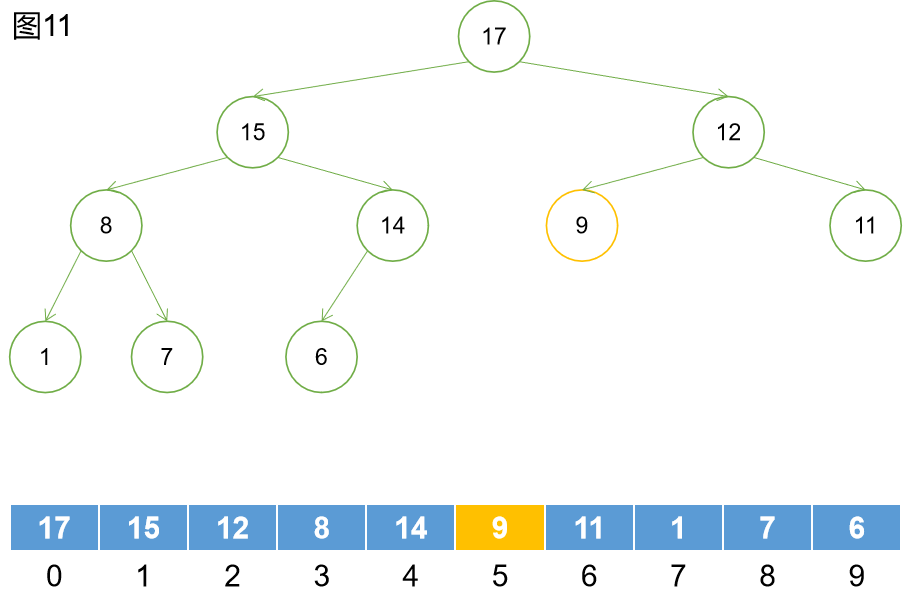
如圖11,9節點繼續下沉最終和其左孩子12交換後,再沒有孩子節點。此次過程的下沉操作完成。下沉操作的時間複雜度為O(logn)
程式碼實現仍然是非常簡單
1 /** 2 * 取出堆中最大元素 3 * 時間複雜度 O(logn) 4 * @return 5 */ 6 public E extractMax(){ 7 E ret = findMax(); 8 this.data.swap(0, (data.getSize() - 1)); 9 data.removeLast(); 10 siftDown(0); 11 return ret; 12 } 13 14 /** 15 * 下沉操作 16 * 時間複雜度 O(logn) 17 * @param k 18 */ 19 public void siftDown(int k){ 20 while(leftChild(k) < data.getSize()){// 從左節點開始,如果左節點小於數組長度,就沒有右節點了 21 int j = leftChild(k); 22 if(j + 1 < data.getSize() && get(j + 1).compareTo(get(j)) > 0){// 選舉出左右節點最大的那個 23 j ++; 24 } 25 if(get(k).compareTo(get(j)) >= 0){// 如果當前節點大於左右子節點,循環結束 26 break; 27 } 28 data.swap(k, j); 29 k = j; 30 } 31 }
3.4、Replace和Heapify
Replace操作呢其實就是取出堆頂元素然後新插入一個元素。根據我們上面的總結,大家很容易想到。返回堆頂元素後,直接將該元素置於堆頂,然後再進行下沉操作即可。
1 /** 2 * 取出最大的元素,並替換成元素 e 3 * 時間複雜度 O(logn) 4 * @param e 5 * @return 6 */ 7 public E replace(E e){ 8 E ret = findMax(); 9 data.set(0, e); 10 siftDown(0); 11 return ret; 12 }
Heapify操作就比較有意思了。Heapify本身的意思為“堆化”,那我們將什麼進行堆化呢?根據其存儲結構,我們可以將任意一個數組進行堆化。將一個數組堆化?what?一個個向最大二叉堆中插入不就行了?呃,如果這樣的話,需要對每一個元素進行一次上浮時間複雜度為O(nlogn)。顯然這樣做的話,時間複雜度控制的不夠理想。有沒有更好的方法呢。既然這樣說了,肯定是有的。思路就是將一個數組當成一個完全二叉樹,然後從最後一個非葉子節點開始逐個對飛葉子節點進行下沉操作。如何找到最後一個非葉子節點呢?這也是二叉堆常問的一個問題。相信大家還記得前面我們說過parent(i) = (child(i)-1)/2。這個公式是不分左右節點的哦,自己可以用程式碼驗證一下,在前面的parent()方法中也有注釋解釋了。那麼最後一個非葉子節點其實就是 (arr.size()-1)/2即可。
接下來我們通過圖示描述一下這個過程,假如我們將如下數組進行堆化

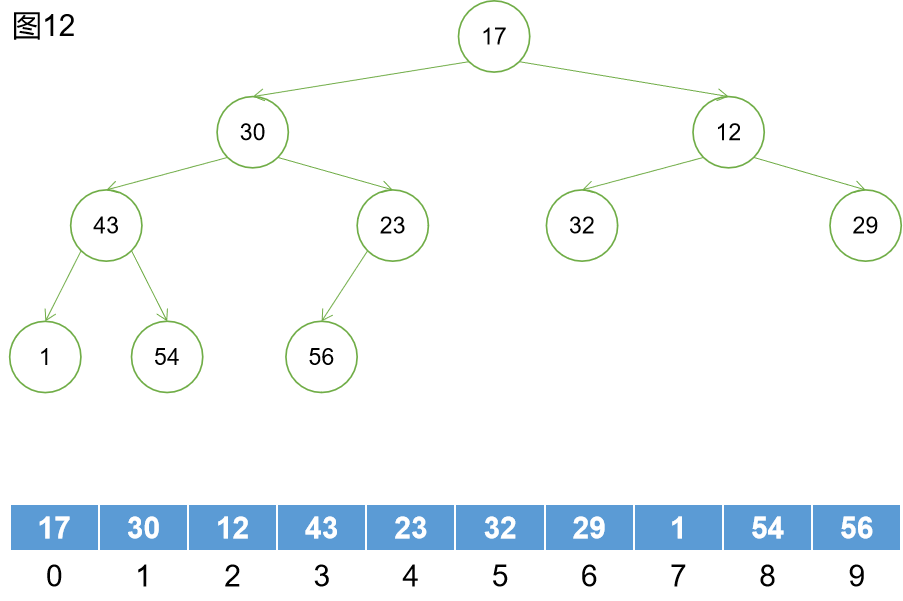
第一步:轉化為一棵完全二叉樹,如圖12所示。
第二步:找到最後一個非葉子節點,如圖13所示。這裡我們將還未調整的非葉子節點設為黃色,將即將要調整的置為綠色。調整完成的置為綠邊圓。
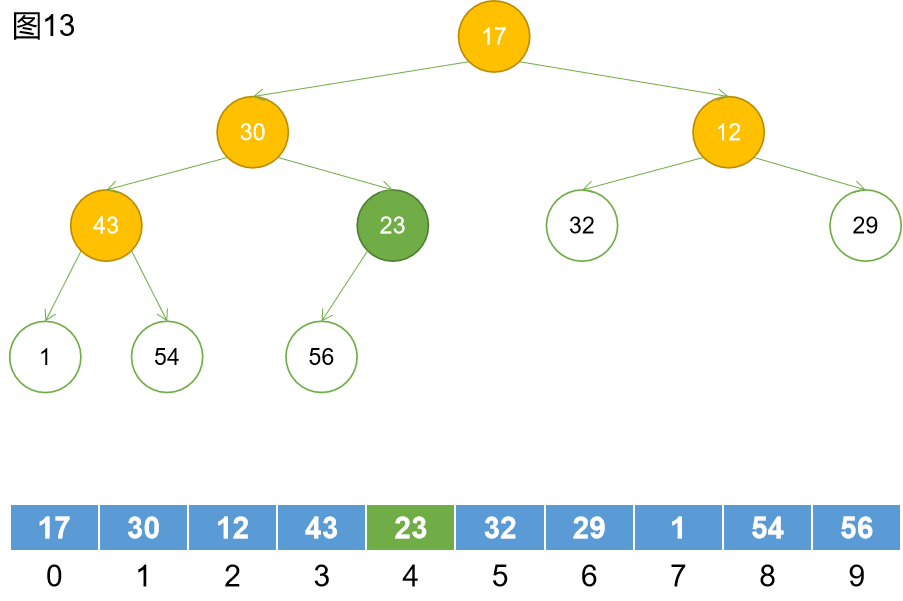
第三步:下沉,非葉子節點和左右孩子進行比較,選出最大的孩子節點進行交換。交換結果如圖14所示

第四步:找到下一個非葉子節點。
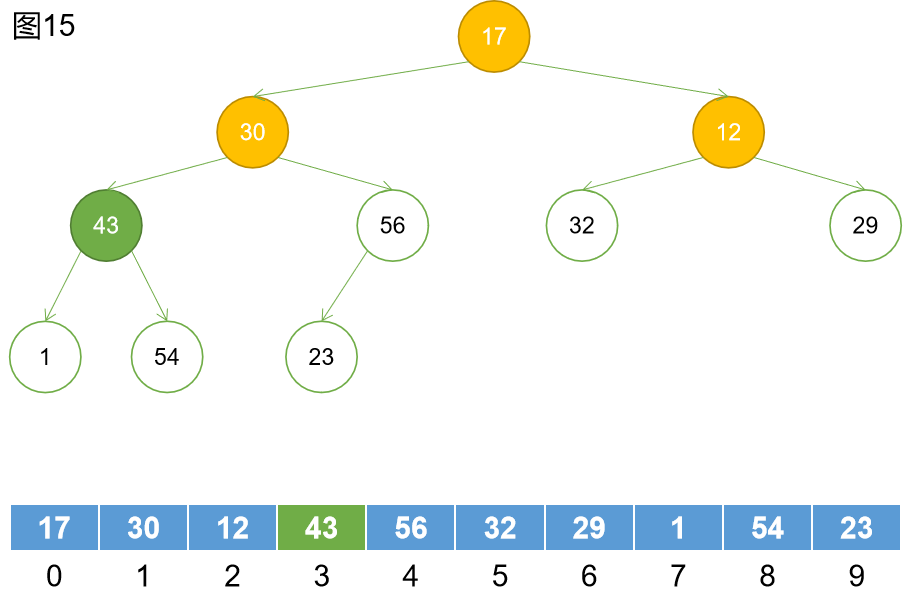
第五步:下沉。
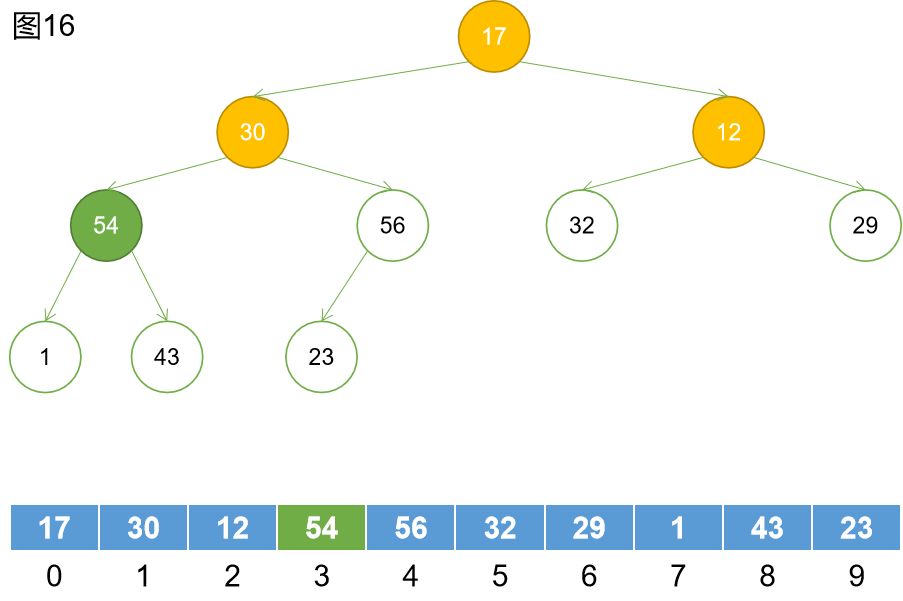
第六步:找到下一個非葉子節點。
第七步:下沉。
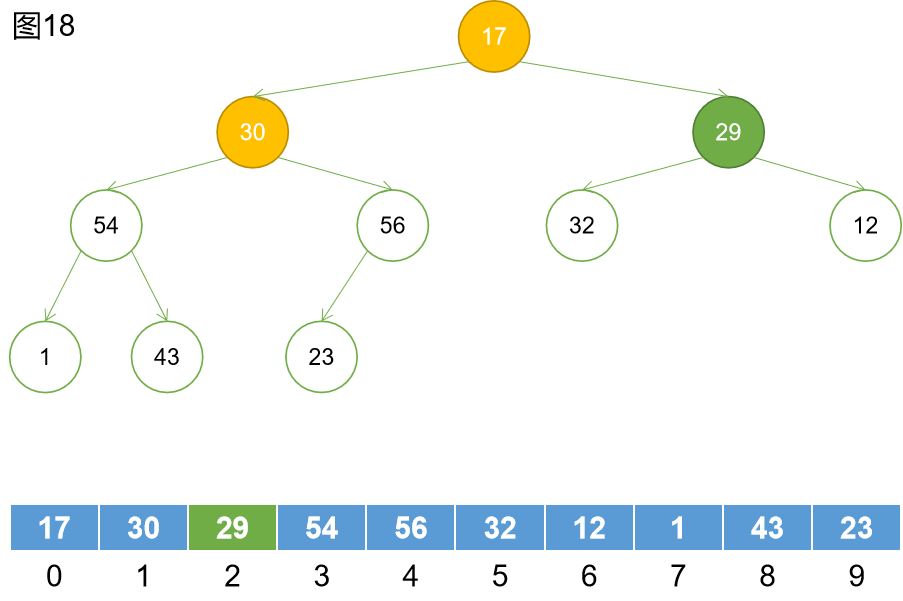
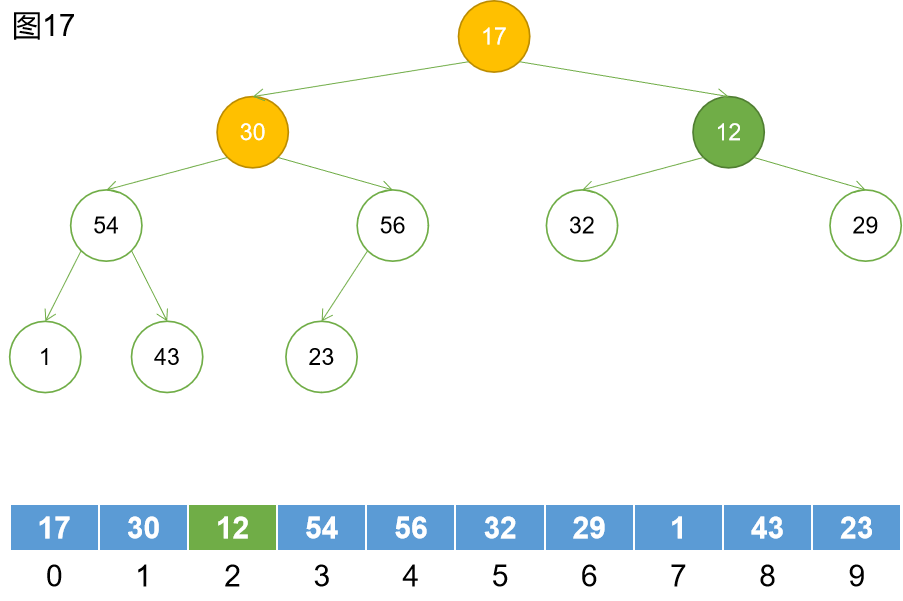
第八步:找到下一個非葉子節點。
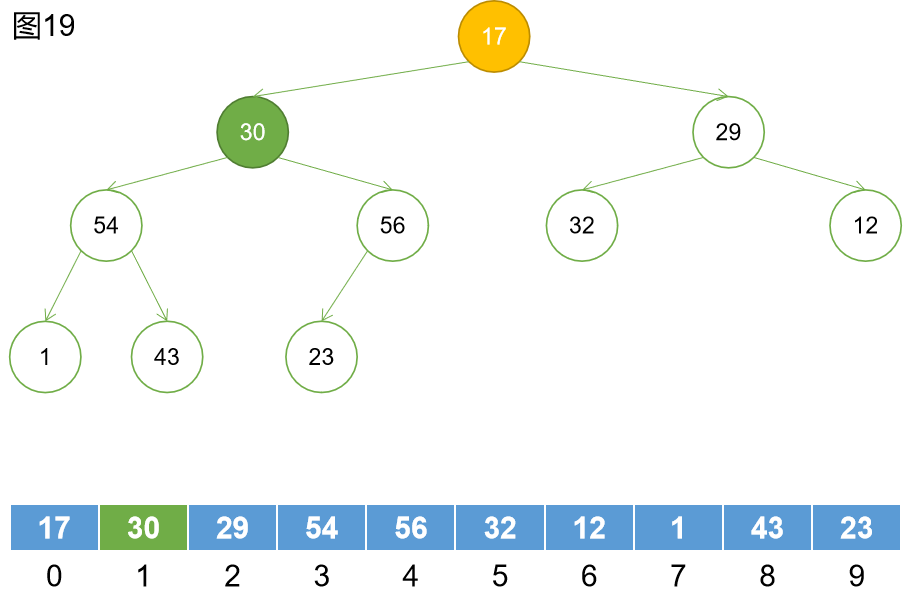
第九步:下沉。30節點下沉到56元素的位置,然後繼續下沉,但是發現大於23,下沉結束。
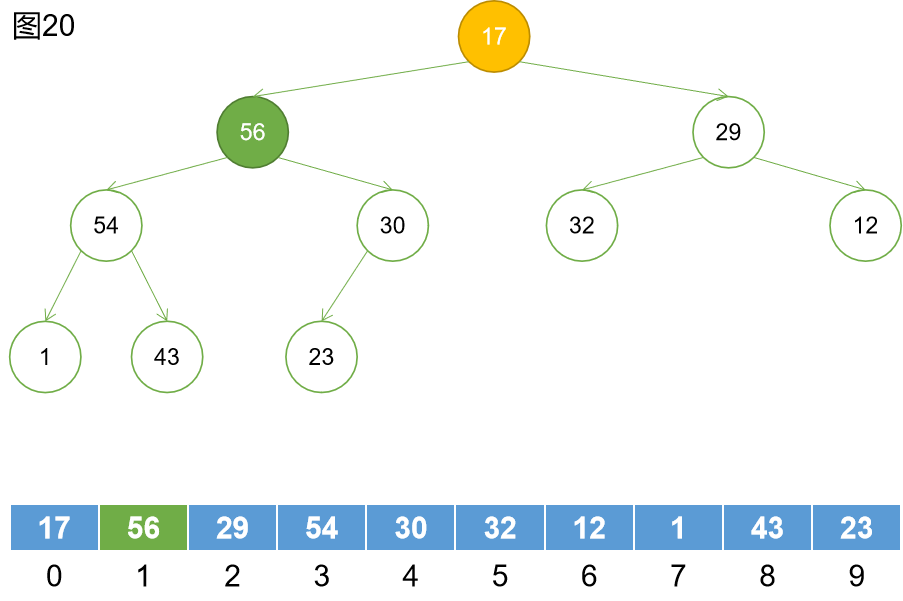
第十步:找到下一個非葉子節點。
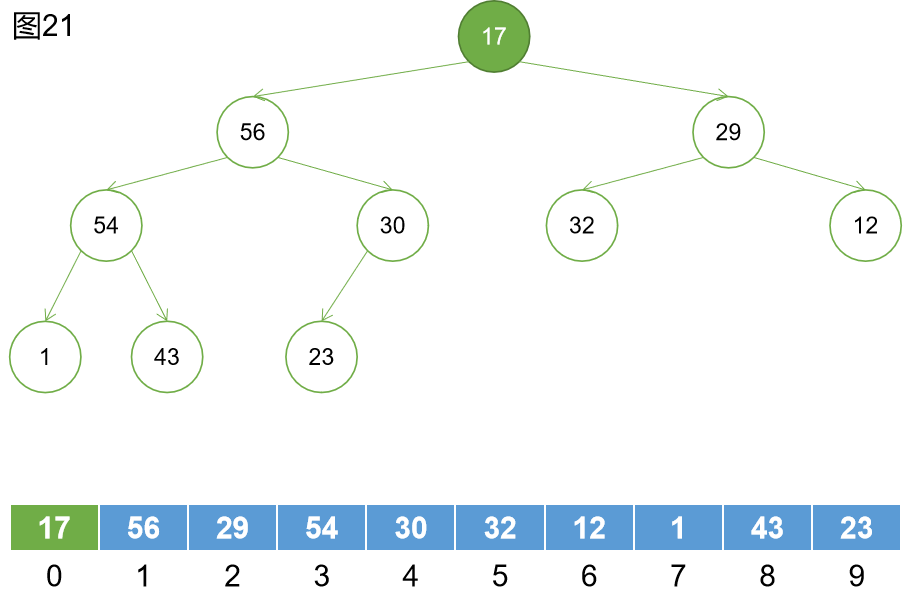
第十一步:下沉。對17節點進行下沉操作,直到其直到適合自己的位置。
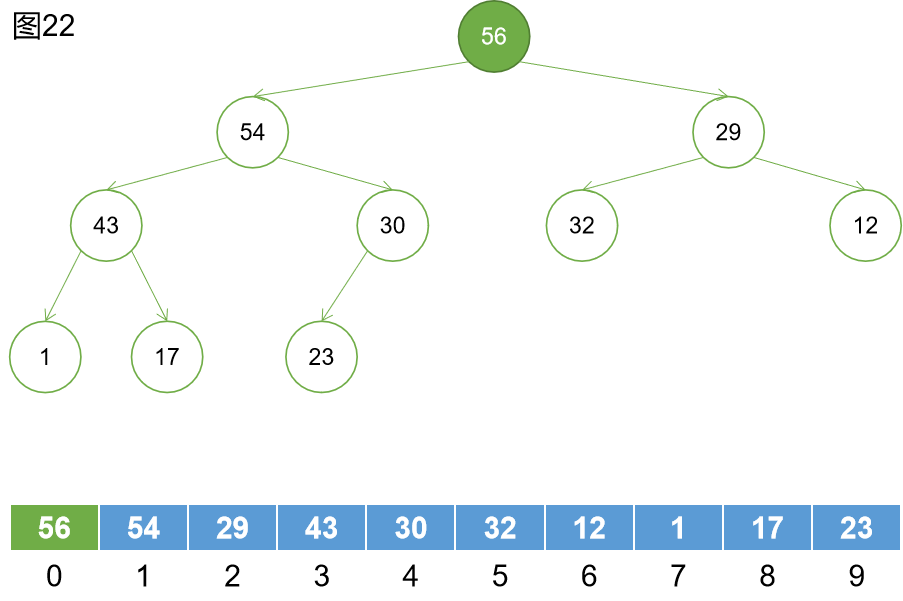
Heapify的整個過程就完成了。時間複雜度控制在了O(n)。
程式碼實現非常的簡單。
1 /** 2 * Heapify 3 * @param arr 4 */ 5 public MaxHeap(E[] arr){ 6 data = new Array<>(arr); 7 for(int i = parent(arr.length - 1); i >= 0; i --){ 8 siftDown(i); 9 } 10 }
四、完整程式碼
1 /** 2 * 描述:最大堆 3 * 4 * @Author shf 5 * @Date 2019/7/29 10:13 6 * @Version V1.0 7 **/ 8 public class MaxHeap<E extends Comparable<E>> { 9 //使用數組存儲 10 private Array<E> data; 11 public MaxHeap(){ 12 data = new Array<>(); 13 } 14 public MaxHeap(int capacity){ 15 data = new Array<>(capacity); 16 } 17 18 /** 19 * Heapify 20 * @param arr 21 */ 22 public MaxHeap(E[] arr){ 23 data = new Array<>(arr); 24 for(int i = parent(arr.length - 1); i >= 0; i --){ 25 siftDown(i); 26 } 27 } 28 public int size(){ 29 return this.data.getSize(); 30 } 31 public boolean isEmpty(){ 32 return this.data.isEmpty(); 33 } 34 35 /** 36 * 根據當前節點索引 index 計算其父節點的 索引 37 * @param index 38 * @return 39 */ 40 private int parent(int index) { 41 if(index ==0){ 42 throw new IllegalArgumentException("該節點為根節點"); 43 } 44 return (index - 1) / 2;//這裡為什麼不分左右?因為java中 / 運算符只保留整數位。 45 } 46 47 /** 48 * 返回索引為 index 節點的左孩子節點的索引 49 * @param index 50 * @return 51 */ 52 private int leftChild(int index){ 53 return index*2 + 1; 54 } 55 56 /** 57 * 返回索引為 index 節點的右孩子節點的索引 58 * @param index 59 * @return 60 */ 61 private int rightChild(int index){ 62 return index*2 + 2; 63 } 64 65 /** 66 * 向堆中添加元素 67 * 時間複雜度 O(logn) 68 * @param e 69 */ 70 public void add(E e){ 71 // 向數組尾部添加元素 72 this.data.addLast(e); 73 siftUp(data.getSize() - 1); 74 } 75 76 /** 77 * 上浮操作 78 * 時間複雜度 O(logn) 79 * @param k 80 */ 81 private void siftUp(int k) { 82 // 上浮,如果大於父節點,進行交換 83 while(k > 0 && get(k).compareTo(get(parent(k))) > 0){ 84 data.swap(k, parent(k)); 85 k = parent(k); 86 } 87 } 88 89 /** 90 * 獲取 index 索引位置的元素 91 * 時間複雜度 O(1) 92 * @param index 93 * @return 94 */ 95 private E get(int index){ 96 return this.data.get(index); 97 } 98 99 /** 100 * 查找堆中的最大元素 101 * 時間複雜度 O(1) 102 * @return 103 */ 104 public E findMax(){ 105 if(this.data.getSize() == 0){ 106 throw new IllegalArgumentException("當前heap為空"); 107 } 108 return this.data.get(0); 109 } 110 111 /** 112 * 取出堆中最大元素 113 * 時間複雜度 O(logn) 114 * @return 115 */ 116 public E extractMax(){ 117 E ret = findMax(); 118 this.data.swap(0, (data.getSize() - 1)); 119 data.removeLast(); 120 siftDown(0); 121 return ret; 122 } 123 124 /** 125 * 下沉操作 126 * 時間複雜度 O(logn) 127 * @param k 128 */ 129 public void siftDown(int k){ 130 while(leftChild(k) < data.getSize()){// 從左節點開始,如果左節點小於數組長度,就沒有右節點了 131 int j = leftChild(k); 132 if(j + 1 < data.getSize() && get(j + 1).compareTo(get(j)) > 0){// 選舉出左右節點最大的那個 133 j ++; 134 } 135 if(get(k).compareTo(get(j)) >= 0){// 如果當前節點大於左右子節點,循環結束 136 break; 137 } 138 data.swap(k, j); 139 k = j; 140 } 141 } 142 143 /** 144 * 取出最大的元素,並替換成元素 e 145 * 時間複雜度 O(logn) 146 * @param e 147 * @return 148 */ 149 public E replace(E e){ 150 E ret = findMax(); 151 data.set(0, e); 152 siftDown(0); 153 return ret; 154 } 155 }
如有錯誤的地方還請留言指正。
原創不易,轉載請註明原文地址:https://www.cnblogs.com/hello-shf/p/11393655.html
