【抓取】6-DOF GraspNet 論文解讀

2020 年 12 月 1 日
筆記
抓取

【抓取】6-DOF GraspNet 論文解讀

【注】：本文地址：【抓取】6-DOF GraspNet 論文解讀
若轉載請於明顯處標明出處。

前言

這篇關於生成抓取姿態的論文出自NVIDIA 。我在讀完該篇論文後我簡單地對其進行一些概述，如有錯誤紕漏請指正！

論文概要

生成抓握姿勢是機器人物體操縱任務的關鍵組成部分。在本工作中，作者提出了抓取生成問題，即使用變分自動編碼器對一組抓取進行取樣，並利用抓取評估器模型對取樣抓取進行評估和微調細化。抓取取樣器和抓取refine網路都以深度相機觀察到的三維點雲作為輸入。作者評估了在模擬和現實世界機器人實驗中的方法。其方法在具有不同外觀、尺度和權重的各種常用對象上獲得88%的成功率。作者直接在模擬環境中訓練而在現實場景下進行實驗測試，這其中沒有任何額外的步驟。

整體網路概述

整體網路結構如下圖：

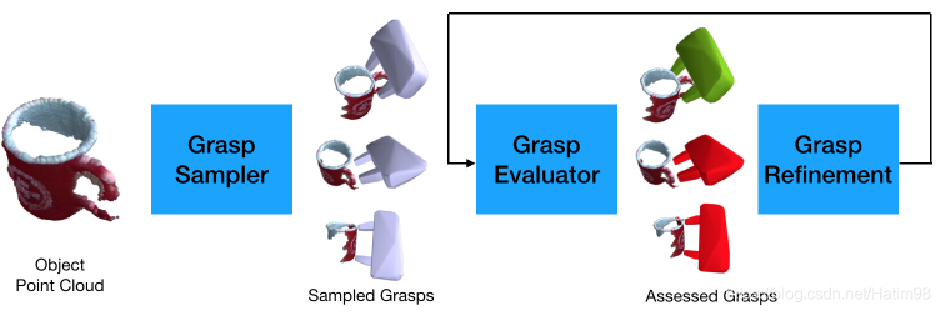
首先，輸入三維點雲，通過 Grasp Sampler 也就是抓取取樣網路，得到多個抓取；然後通過一個 Grasp Evaluater ，評估上一步生成的抓取的成功與否；在評估這一步中，通過 Grasp Refinement 將估計的抓取結果進行微調，使其更貼近於合理抓取，進一步地增大了抓取的成功率。

下面具體來講一下每一部分。

Variational Grasp Sampler

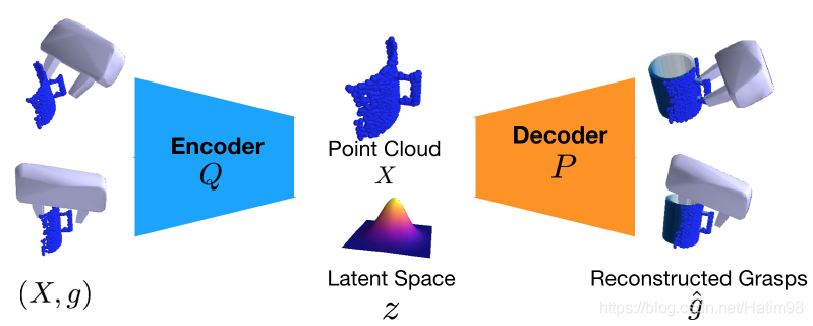
抓取取樣網路本質上是一個VAE，也就是變分自編碼器。輸入 \(X\) 是對原始目標三維點雲取樣得到的各個視角下的目標點雲， \(g\) 其實就是抓取姿態，也就是抓取器在目標坐標系下的 \(R\) 和 \(T\)。通過VAE的編碼器Q，將輸入編碼到隱層空間，得到低維度的隱層變數 \(z\) ，使其滿足單位高斯分布；然後再通過對隱層變數 \(z\) 解碼，得到與輸入相近的 \(g\) 。整個VAE的訓練過程就是讓z盡量服從上面所說的單位高斯分布，所以在測試的時候，去掉Encoder，直接在單位高斯分布中隨機取樣，取代了需要編碼得到的隱層變數 \(z\) ，再加上輸入點雲 \(X\) ，就可以得到網路所認為的絕對正確的重建抓取 \(\hat{g}\) 。在訓練中，VAE的損失函數如下：

\[\mathcal{L}_{\mathrm{vae}}=\sum_{z \sim Q, g \sim G^{*}} \mathcal{L}(\hat{g}, g)-\alpha \mathcal{D}_{K L}[Q(z \mid X, g), \mathcal{N}(0, I)]
\]

該式採用隨機梯度下降優化。對於每個mini-batch，點雲 \(X\) 從隨機視點觀察取樣。對於取樣點雲 \(X\) ，抓取 \(g\) 從Ground Truth集合\(G^{*}\)採用分層取樣。
上式中的 \(\mathcal{L}(g, \hat{g})\) 具體式子如下：

\[\mathcal{L}(g, \hat{g})=\frac{1}{n} \sum\|\mathcal{T}(g ; p)-\mathcal{T}(\hat{g} ; p)\|_{1}
\]

此式約束重建抓取與輸入抓取相近。 \(\mathcal{T}(\cdot ; p)\) 是機器人夾持器上一組預定義點 \(p\) 的變換，什麼意思呢？換句話說就是，在目標坐標系中，把抓取器的模型通過 \(R\) 和 \(T\) 作變換，從而轉變為目標坐標系下的抓取器點雲。

Grasp Pose Evaluation

因為前一步生成的抓取在網路看來他一定是正確的（因為他認為自己的 \(z\) 服從單位高斯分布，那麼從單位高斯分布中取樣重建出的 \(\hat{g}\) 一定是正確的抓取），所以實際上要想知道生成的抓取在我們看來是否可行，就還需要加一個判斷。因此作者在抓取取樣網路之後加了個抓取姿態評估網路。

整個評估網路實質上是一個二分類網路，輸入是目標和抓取器的合成渲染點雲 \(X \cup X_{g}\) ，輸出是成功率 \(s\) 。利用交叉熵損失優化抓取評價網路：

\[\mathcal{L}_{\text {evaluator }}=-(y \log (s)+(1-y) \log (1-s))
\]

式中 \(y\) 是抓取的Ground Truth二進位標籤，1/0 代表成功/失敗。

在訓練中採取了hard negative mining（有翻譯叫他難負例挖掘），簡單倆說就是建立了一個錯題集 \(G^{-}\) ：

\[G^{-}=\left\{g^{-} \mid \exists g \in G^{*}: \mathcal{L}\left(g, g^{-}\right)<\epsilon\right\}
\]

在訓練過程中，這個錯題集中包含：

從一組預先生成的負抓取中取樣 \(g^{-}\) ;
或者通過隨機擾動正抓取集 \(G^{*}\) 中的 \(g\) 使夾持器的網格要麼與物體網格碰撞，要麼將夾持器網格遠離物體。

前面說完了，這一部分我覺得才是重點部分！通過前面的評估，已經得到了一些成功和失敗的抓取例子，那麼怎麼提高成功率呢？換句話說，怎麼讓估計出來的抓取 \(g\) 更好呢？

為了達到這個目的，作者想到了一個巧妙的辦法，既然評估網路中的 \(s\) 越大代表越可能成功，那麼使得這些 \(s\) 都儘可能地變大並且趨近於1也就能讓抓取 \(g\) 更好了唄~

實際上這就代表了能讓 \(s\) 相對於 \(g\) 的函數 \(S\) 值變大的方向。這個方向就是 \(S\) 相對於 \(g\) 的梯度方向，也就得到了下面的式子：

\[\Delta g=\frac{\partial S}{\partial g}=\eta \times \frac{\partial S}{\partial \mathcal{T}(g ; p)} \times \frac{\partial \mathcal{T}(g ; p)}{\partial g}
\]

如果上面不理解，也沒關係，有點繞口。我說一個一維曲線的例子。

如上圖所示，\(y=f(\theta x)\) 代表擬合出來的曲線，其中 \(\theta\) 代表 \(x\) 的係數（等同於網路的權重參數）。現在假如輸入是 \(x_{1}\) ，輸出是 \(y_{1}\)，然後我已知 \(y_{2}\) 是一個更好更大的輸出值，那麼我就需要改變 \(x\) 的值，讓 \(x_{1}\) 變成 \(x_{2}\) ：

\[x_{2}=x_{1}+\Delta x
\]

那麼變化量 \(\Delta x\) 怎麼得到呢？在這個例子里， \(x\) 變化無非兩種情況，要麼變大要麼變小，要想知道我們需要他變大還是變小，只需要讓函數 \(f\) 對 \(x\) 求導就得到了斜率，斜率就指明了 \(x\) 變化方向。在這個例子裡面 \(x\) 變化方向是 \(x\) 軸的正方向。得到了變化方向我們乘上一個步長 \(\eta\) 就得到了我們需要的變化量 \(\Delta x\) ：

\[\frac{\partial f}{\partial x} \cdot \eta=\Delta x
\]

Experiments

實驗部分暫時不說了，作者說這抓取效果就是好反正。其他自對比實驗也很有意義，有空再更。

Tags: 抓取