在開始正式的介紹之前，先做一個簡單的定義，以免產生歧義：

1、本文中的“數據點”是指：

1）對於直線擬合、平面擬合等問題，即為相應的二維/三維坐標點；

2）對於從匹配點中估計基本矩陣、單應矩陣等問題，即為一對匹配點坐標級聯組成的向量。

一、RANSAC之前

RANSAC在1981年被Martin A. Fischler and Robert C. Bolles兩人提出，以解決給定點集的模型估計問題。在現實應用中，我們經常遇到的情況是：給定的點集中存在錯誤的點。傳統的模型估計方法，大都採用所有的點進行模型最小二乘的擬合，這種方法往往容易受野點影響而得到錯誤結果（相當於陷入局部最優）。該最小二乘法的一種變種是，首先用所有點估計模型，而後剔除誤差較大的點，而後再次估計模型，以此迭代。然而，由於野點的影響，往往會導致最開始估計的模型不準確，從而導致正確的點被剔除掉，最終導致模型估計的失敗。下面是一個例子：

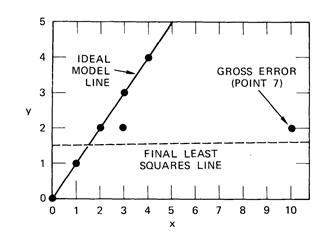
由於點7的影響，導致正確的點被剔除，最終擬合的直線為虛線，而不是正確的實線。

二、RANSAC之1.0版本

RANSAC方法為第一個方法，採用最少能決定模型的點進行模型估計的方法，最原始的方法被描述為：

整個演算法被分為三步：

1） 從所有的數據中取樣n個點，以能確定出模型；

2） 利用取樣點計算模型；

3） 利用模型來確定其他點是否是內點；如果內點率達到指定值，演算法終止，並用所有內點優化模型；否則，繼續上述過程，直到達到指定的迭代次數，此時將最高內點率對應的模型作為最終模型。

上述思路簡潔明了，其核心思想就是：待求解的模型，應該是能同時使最多數據點都符合模型。從這一思想從發，其實可以有另一條不同的思路，後續我會進一步介紹。

三、RANSAC 1.0版本剖析

下面讓我們回顧下該方法，看該方法在具體應用中，還需要解決哪些問題：

演算法第一步，從數據中取樣n個點，這裡要求n為能確定模型的最小的數據量，那麼該選取怎樣的取樣準則？從所有數據中取樣，還是僅僅從部分數據（總數據的一個子集）中進行取樣？每個數據被採集的可能性是否相同？採取隨機取樣，還是按一定順序進行取樣？是否需要避免同一組數據被重複取樣，如果需要，該如何避免？這裡先給出通常的做法，更加細緻的分析也留到後續。通常情況下，我們在所有數據中進行隨機取樣，且所有數據每次被取樣的可能性是一樣的，而且我們通常不考慮兩次取樣得到的樣本是重複的。

演算法第二步，利用取樣數據計算模型。我們知道，在第一步中，我們要求取樣點儘可能少，同時我們也知道，當數據點存在雜訊（通常考慮為高斯雜訊）時，樣本點的數目越多，求解的模型越準確。這就意味著我們此刻求解的模型不夠準確，那麼這個不夠準確的模型，是否能夠用來判斷其他點是否是內點？其次，如果我們待求解的問題，無法用一個模型，或者無法用一個僅包含若干個參數的模型進行表達，此時是否還能使用“最大一致性”的思路？針對第一個問題，我們通常認為雖然模型存在誤差，但是在後續內點判斷中，我們設定一定的誤差閾值，因此能夠用該模型來近似最終模型。同時，一些RANSAC的改進，採用“局部優化”技術來一定層度解決這一問題，關於該方法的討論，同樣會在後續，進行詳細的剖析。針對第二個問題，有一些無模型的“最大一致性估計”方法，同樣也留待後續介紹。

演算法第三步，首先，利用求解的模型確定其他點是否為內點。一個重要的問題是，如何判斷其他點是否為內點？通過其他點與模型的符合程度？那麼如何設置這樣一個閾值？有時一個數據是否為內點（例如兩個數據點相衝突，不可能同時為內點。這種情況會發生在：根據兩張圖特徵點匹配，求解其基礎矩陣時，如果A圖中的兩個點，匹配到B圖中的同一個點），還與其他數據相關，那麼此時如何考慮數據間的關聯？

其次，“如果內點率達到指定值，則終止演算法”，那麼如何設置這樣一個閾值？因為對於一組數據，通常情況下我們是無法知道其最大內點率。（但問題也不是絕對，我們也可以事先求解出最優模型對應的內點率。哈哈，是不是很crazy，這也留待後續的剖析。）因此，這一迭代的終止條件，現在的RANSAC演算法中，已經很少見了。我們通常採用一定置信度下，達到能夠保證至少一次所有的取樣點都為內點的最少取樣次數，作為終止條件。

最後，如何確定最少的取樣次數。原文中提出了兩種方案。假設在一次取樣中，所有點都為內點的概率為p，那麼“所有取樣點都為內點首先發生在第k次取樣”這一事件服從幾何分布（參考射擊時第k次才命中這一問題），於是：

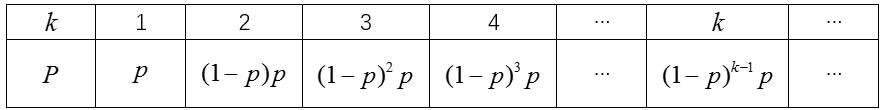
原文方案一：求解k的期望值和方差，採用期望值加上2到3倍方差，作為取樣次數。這種方案，可以理解為求解分布的“上分位數”，以保證以一定“所有取樣點都為內點”在進行k次取樣後發生過。

原文方案二：如果要求第 次取樣後，至少一次“所有取樣點都為內點”的概率大於 那麼：

由此，

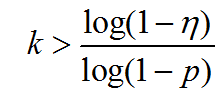
這裡一次取樣中所有點都為內點的概率為：

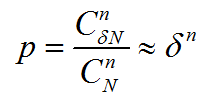
其中N為總數據量，n為最小取樣數，為內點率。

在此，我們可以看出，為什麼選取最少的樣本點進行模型估計。因為，取樣量每增加1，對應需要進行的取樣次數就增加很多，尤其是在內點率很低的情況下，這種情況尤其嚴重。

寫到這裡，我們已經對RANSAC最初版本進行了詳細的介紹，同時我們很具體剖析了其各個步驟可能面臨的問題。針對這些問題，後續衍生出了很多RANSAC的變種，我們將在後續進行具體的介紹。

參考文獻：

[1]   Fischler M A . Readings in Computer Vision || Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J]. Readings in Computer Vision, 1987:726-740.