演算法筆記·並查集

• 2019 年 10 月 3 日
• 筆記

並查集

並查集我個人認為一種用來處理某些特殊數據結構的演算法，其優點在於程式簡短，能夠快速簡潔的表達出點與點，數於數之間的關係。

這種演算法有兩個操作，合併與查詢

• 合併：能夠高時效的將某一些符合題目要求的數據合併在一個集合中
• 查詢：能夠高時效的查詢某個指定數據是否存在於某個集合之中，或者是計算滿足題目要求的集合數量

那麼這個演算法是如何運作的呢？

接下來我們看幾道例題

例題1.親戚

Luogu傳送門

這是一道十分簡單的並查集入門題，這裡用來講述並查集的運作思路。

根據題意，如果B是A的親戚，C是B的親戚，那麼ABC三個人互為親戚，也就是說ABC三個節點可以被放置在同一個集合當中，為了方便表述，我們可以認為這是一顆樹，A是根，B是A的子節點，C是B的子節點。

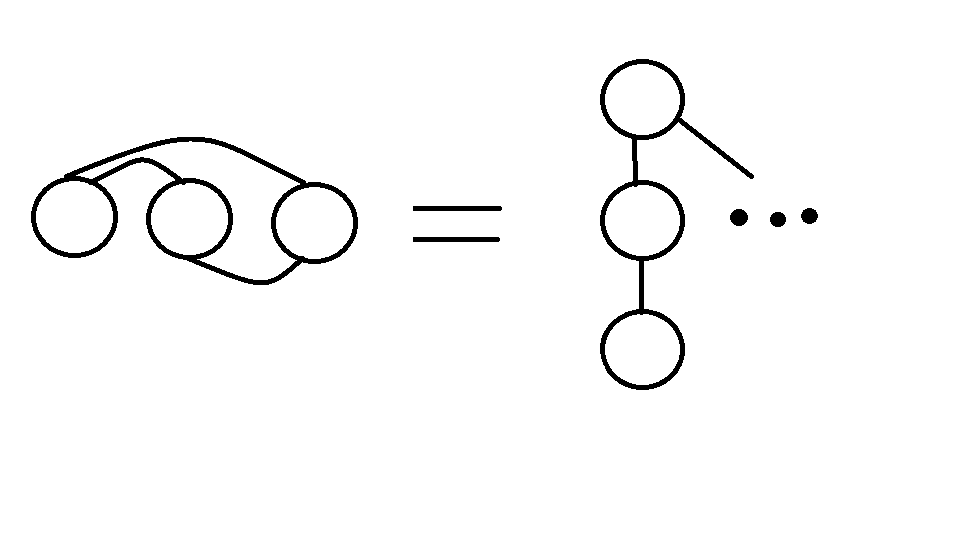
由此，我們便可以利用並查集，將有親戚關係的兩個節點，進行建邊，即將兩個有親戚關係的節點所處的集合進行合併，在查詢時，只要利用一個遞歸，不停向上詢問，直到問到自己的根節點，如根節點相同，便是有親戚關係。

但是，還有一個問題，如此下來某個點都向上詢問一遍，將會耗費大量的時間，那麼何來高時效之說呢？

這裡我們需要對並查集做一個優化，使其能更快的計算出自己的根節點，我稱之為縮點，將所有有關係的點都進行直接掛靠，也就是說，構造出一顆深度為2的樹，如圖。

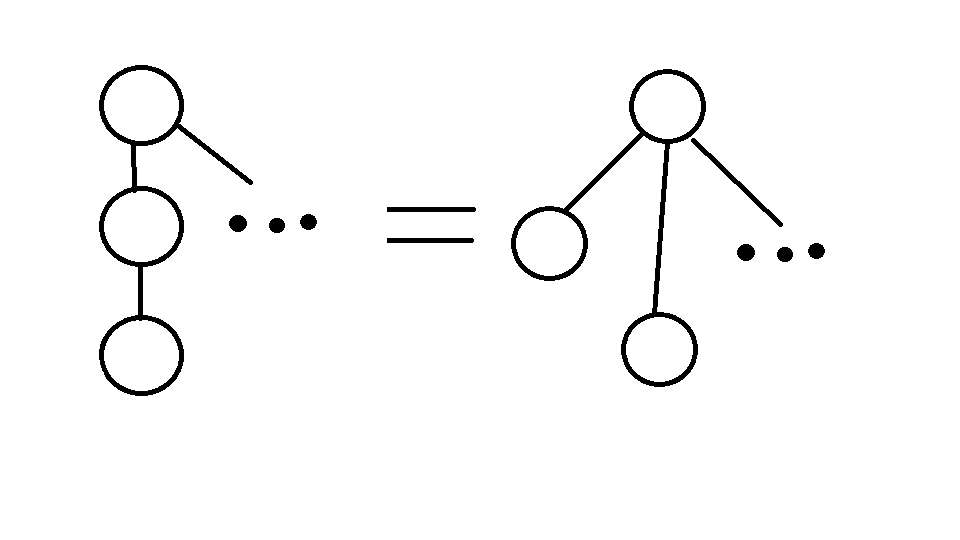
如此一來，在查詢的時候就可以直接訪問到自己的根節點了。

#include<stdio.h>  #include<algorithm>  int n,m,a,b,fa[10005];  int find(int x){   //查詢函數      if(fa[x]!=x) fa[x]=find(fa[x]);  //縮點：反覆向上詢問，詢問到根節點才賦值      return fa[x];  }  int main(){      scanf("%d%d",&n,&m);      for(register int i=1;i<=n;i++){fa[i]=i;} //初始化，開始時每個節點都是一個根節點      for(register int i=1;i<=m;i++){          scanf("%d%d",&a,&b);          a=find(a);b=find(b);          if(a!=b) fa[b]=fa[a];  //合併      }      int Q;      scanf("%d",&Q);      for(register int i=1;i<=Q;i++){          scanf("%d%d",&a,&b);          if(find(a)==find(b)) printf("Yesn");  //根節點相同          else printf("Non");      }      return 0;  }  

通過這道題目,我們可以了解了並查集的基本運行思路，其實很多題的基本程式碼也是依照這個作為模板，不過在此基礎上作出一些變化。

例題2.黑社會團伙

Luogu傳送門

由題意可知，這題與上一題大題框架一樣，變化的地方在於

• 求集合數量
• 多出了新的概念，我敵人的敵人也是我的朋友

由新的概念便可以引申出許多新的關係，稍作整理，就有如下幾條

• 我朋友的朋友是我的朋友
• 我朋友的敵人是我的敵人
• 我敵人的敵人是我的朋友
• 我敵人的朋友是我的敵人

這時如果僅用原來的單個集合進行計算，就會發現難以表現如上的4種情況，在上一題中，只存在兩種情況，是我的親戚，或者不是，而在該例題中，存在3種情況，是朋友，是敵人，或者兩者沒有關係。

在上一題中我們用了一棵圖來描述人與人之間的親戚關係，兩點之間有建邊即為親戚關係，無建邊則沒有關係，也就是將有親戚關係的集合互相合併，那麼在這一題中，我們依然可以沿用這樣的思路，不過這題我們需要兩張圖，一張用以表現朋友關係，一張用以表現敵人關係，兩張圖中的節點可以互相映射。

那麼接下來就是編寫程式碼，我們個可以使用n的空間表示朋友，n的空間表示敵人，總共使用2*n的空間。

如何編寫兩棵樹之間節點互相的關係映射，假設兩人A,B，當A與B是朋友時，在朋友關係圖中將B點與A點建邊，另外在B的敵人關係圖中查找B的敵人，在敵人關係圖中將該節點與A節點建邊。

假設A與B是朋友，A與C是朋友，B與D是敵人，如圖

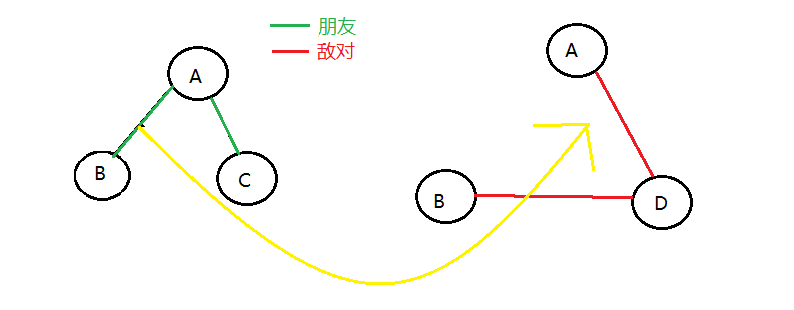
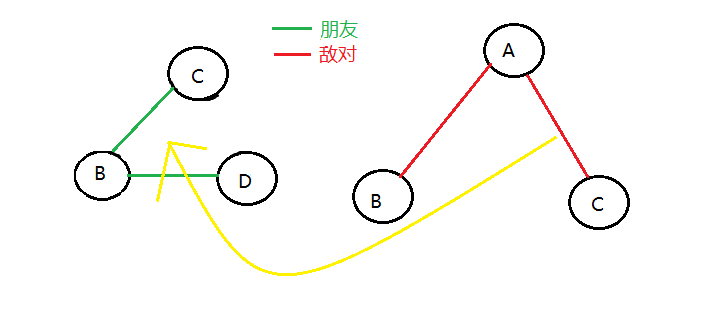
反之，亦可成立，即A與B是敵人時，將B點與A點在敵人關係樹中建邊，同時，在敵人關係樹圖中尋找與A有關的節點(除了B)，在朋友關係圖中將該節點與B節點建邊。

假設A與B是敵人，A與C是敵人，B與D是朋友，如圖

假設表示朋友的集合是P，P的反集即表示敵人的集合是D

則用數學的集合語言來表示就是

• A與B是朋友：
  1.(P_A cup P_B) 朋友的朋友是朋友
  2.(D_A cup D_B) 朋友的敵人是敵人

• A與B是敵人：
  1.(F_A cup P_B) 敵人的敵人是朋友
  2.(D_A cup F_B) 敵人的朋友是敵人

然後，再利用縮點來提高程式碼的運行效率，就可以達到「Ac的真實了！」

但是如何實現上述的關係轉化？

Fa數組開2*N空間，然後1對應n+1，2對應n+2，3對應n+3，以此類推，也就是1—n表示集合P，n+1—n+n表示P的反集，集合D，而計算團伙數量只要枚舉一下所有的點，看看有幾個點的fa數組沒有被修改過，因為縮點以後，根節點必定對應他自己，所以計算根節點的數量即為集合數量。

上程式碼！

#include <stdio.h>  #include <algorithm>  #include <iostream>  int fa[50005];  int find(int a){      if(fa[a]!=a) fa[a]=find(fa[a]);  //縮點      return fa[a];  }  int main(int argc, char const *argv[]){      int n,m;scanf("%d%d",&n,&m);      for (register int i = 1; i <= 2*n; ++i){ fa[i]=i; }  //初始化      for (register int i = 1; i <= m; ++i){          char cmd;std::cin>>cmd;          int a,b;scanf("%d%d",&a,&b);          if (cmd =='F'){              fa[find(a)]=find(b);   //朋友集合相併              fa[find(a+n)]=find(b+n);  //敵人集合相併          }else{              fa[find(a+n)]=find(b);  //敵人的朋友是敵人              fa[find(b+n)]=find(a);  //敵人的敵人是朋友          }      }      int ans=0;      for (register int i = 1; i <= n; ++i){          if(fa[i]==i) ans++;  //枚舉集團數量      }      printf("%d",ans);      return 0;  }

之後還有例題就再擴充吧www

通過上面的例題我們可以看到，並查集的本質其實就是求同存異，將具有某一相同特性或關係的數據合併在同個集合之中，並查集的程式碼量並不大，但是卻能夠清楚的描述出我們所需要的數據關係。

我個人認為並查集是一種十分優秀的演算法，簡短高效，值得去了解和鑽研，問題就是你能不能去合理的運用，用得好就是一把利器，削鐵如泥。

點贊+關注是閣下對我最大的鼓勵！