洛谷 P2101 命運石之門的選擇 （分治)

  • 2020 年 11 月 21 日
  • 筆記

P2101 命運石之門的選擇 （分治)

介紹

El Psy Congroo

題目鏈接

沒錯，作為石頭門廚，怎麼能不做石頭門的題呢？(在搜石頭門的時

候搜到了本題)

本題作為一道分治基礎練習題還是不錯的，雖然看起來挺簡單,但還

是有不少需要思考的地方的。(可能是我太菜了)

分析

我們對本題進行分析，

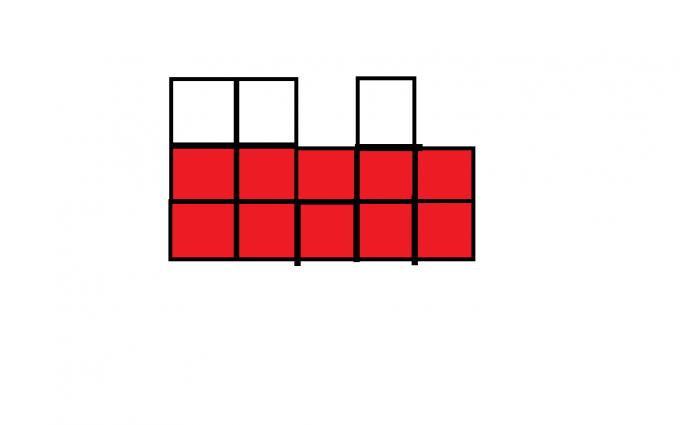
就拿下面這個圖舉例

D3n1rn.md.png

我們首先觀察到了紅色部分，紅色部分是當前所能構成的最大矩形

我們擁有兩種塗色方法，橫著塗和豎著圖，因為塗一次色的代價與塗

色面積無關，所以我們每一次塗色需要儘可能的多塗。

對於紅色部分，顯然，全部採用同一種塗色方法是要比兩

種方法同時採取更優的，因為當我們混用塗色方法時，一定是可以

通過去掉某一次塗色來降低所需代價的。

針對紅色部分，如果我們全部採用豎著塗，因為我們要儘可能的多

塗，所以我們既然可以豎著塗完紅色部分，也可以在同代價下塗完

整個圖，所以我們目前塗完整個圖的代價就是當前圖形的寬度，如

果我們採用橫著圖，塗完整張的總代價就是（該圖形中最低的小矩

形的高度）+（塗完紅色部分以外部分的最小代價）

我們所要求的答案就是這兩種方法的代價最小值

那如何求出塗完紅色部分以外部分的最小代價呢？

這時候就要採用分治思想了，

我們用原圖形減去紅色部分，得到了一個或幾個圖形，我們目前要

求的就是塗完所有新圖形的最小代價，我們針對每一個新圖形都按

先前求原圖形的最小代價的方法處理，最後將其合併即可。

放一下程式碼

#include<cstdio>
#include<cstring>
#include<string>
#include<iostream>
#define int long long
using namespace std;
const int maxn=1e4;
inline int read(){
	int ret=0;
	int f=1;
	char ch=getchar();
	while(ch<'0'||ch>'9'){
		if(ch=='-')	
			f=-f;
		ch=getchar();
	}
	while(ch<='9'&&ch>='0'){
		ret=ret*10+(ch^'0');
		ch=getchar();
	}
	return ret*f;
}
int n;
int m;
int a[maxn];
int slove(int l,int r){
	if(l==r){
		return 1;//邊界
	}
	int t=r-l+1;//目前圖形的寬度
	int minn=0x3f3f3f3f;
	for(int i=l;i<=r;i++){
		if(a[i]<minn){
			minn=a[i];//找到最低矩形的高度
		}
	}
	int ans=minn;
	for(int i=l;i<=r;i++){
		a[i]-=minn;//減掉紅色部分
	}
	int ll=l;
	for(int i=l;i<=r;i++){
		if(a[i]&&!a[i-1])
			ll=i;
		if(a[i]&&(!a[i+1]||i==r)){
			ans+=slove(ll,i);//分治處理
		}
	}
	return min(ans,t);
}
signed main(){
//	freopen("a.txt","r",stdin);
	n=read(); 
	for(int i=1;i<=n;i++){
		a[i]=read();
	}
	cout<<slove(1,n); 
	return 0;
}

這一切都是命運石之門的選擇

VirMach 便宜 VPS

QNews

QNews