自由變形技術（Free-Form Deformation）

• 2019 年 10 月 3 日
• 筆記

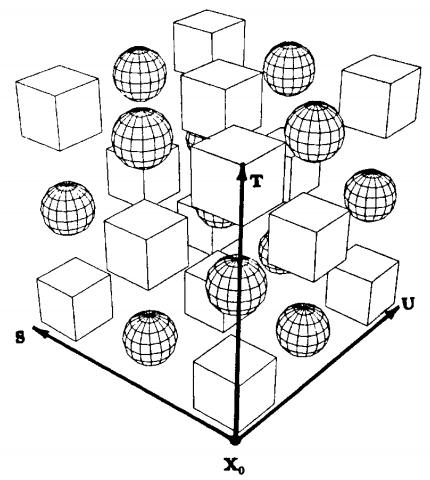
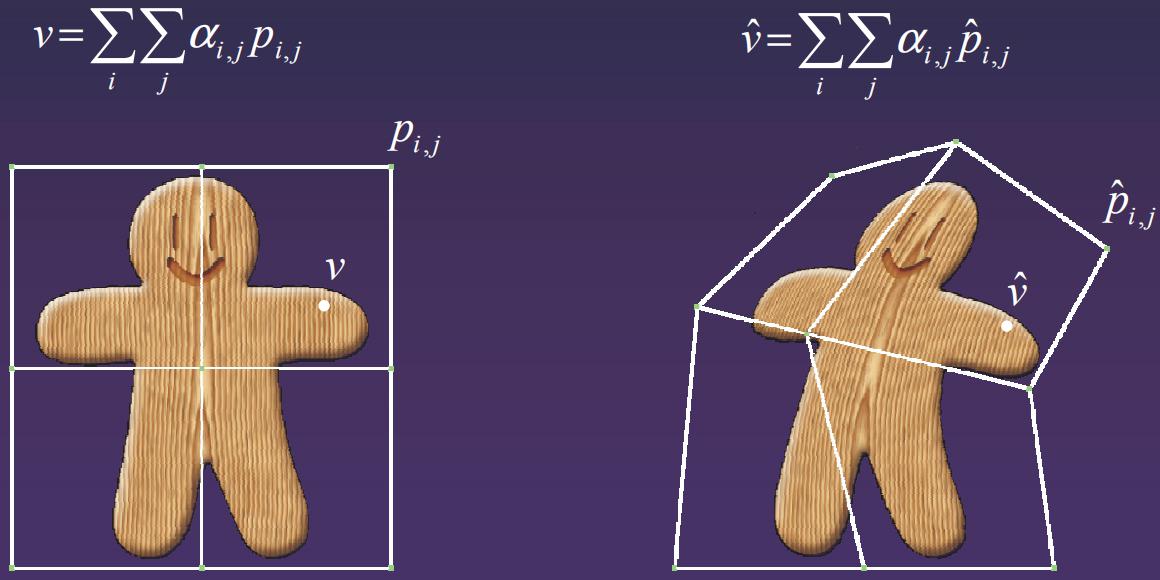
　　自由變形技術Free-Form Deformation是編輯幾何模型的重要手段，它於80年代由Sederberg等人提出，目前許多三維建模軟體中都有這種變形演算法。自由變形方法在變形過程中並不是直接操作幾何模型，而是把幾何模型嵌入到變形空間，然後通過操作變形空間來使得嵌入其中的幾何模型發生變形，如圖所示。

　　自由變形演算法主要過程如下：

　　1. 創建一個平行六面體的變形空間框架，將待變形幾何模型嵌入這個框架中，同時建立局部坐標系，計算幾何模型的頂點在局部坐標系下的坐標：

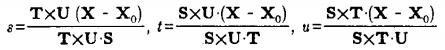
其中，S、T、U可以認為是這個變形框架的3個邊長向量，並且0 < s < 1、0 < t < 1、0 < u < 1。需要注意的是，在變形過程中，幾何模型頂點的局部坐標(s, t, u)都是固定不變的。

　　2. 移動變形框架控制點，利用幾何模型頂點的局部坐標(s, t, u)、控制點世界坐標和Bernstein多項式重新計算幾何模型每個頂點的世界坐標：

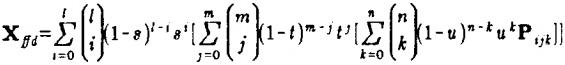
其中P(i, j, k)為框架控制點的新坐標，l、m、n分別為在S、T、U坐標軸上劃分的格子數目。

本文為原創，轉載請註明出處：http://www.cnblogs.com/shushen。

參考文獻：

[1] Sederberg, Thomas W., and Scott R. Parry. “Free-form deformation of solid geometric models.” international conference on computer graphics and interactive techniques 20.4 (1986): 151-160.

[2] https://en.wikipedia.org/wiki/Bernstein_polynomial

附錄

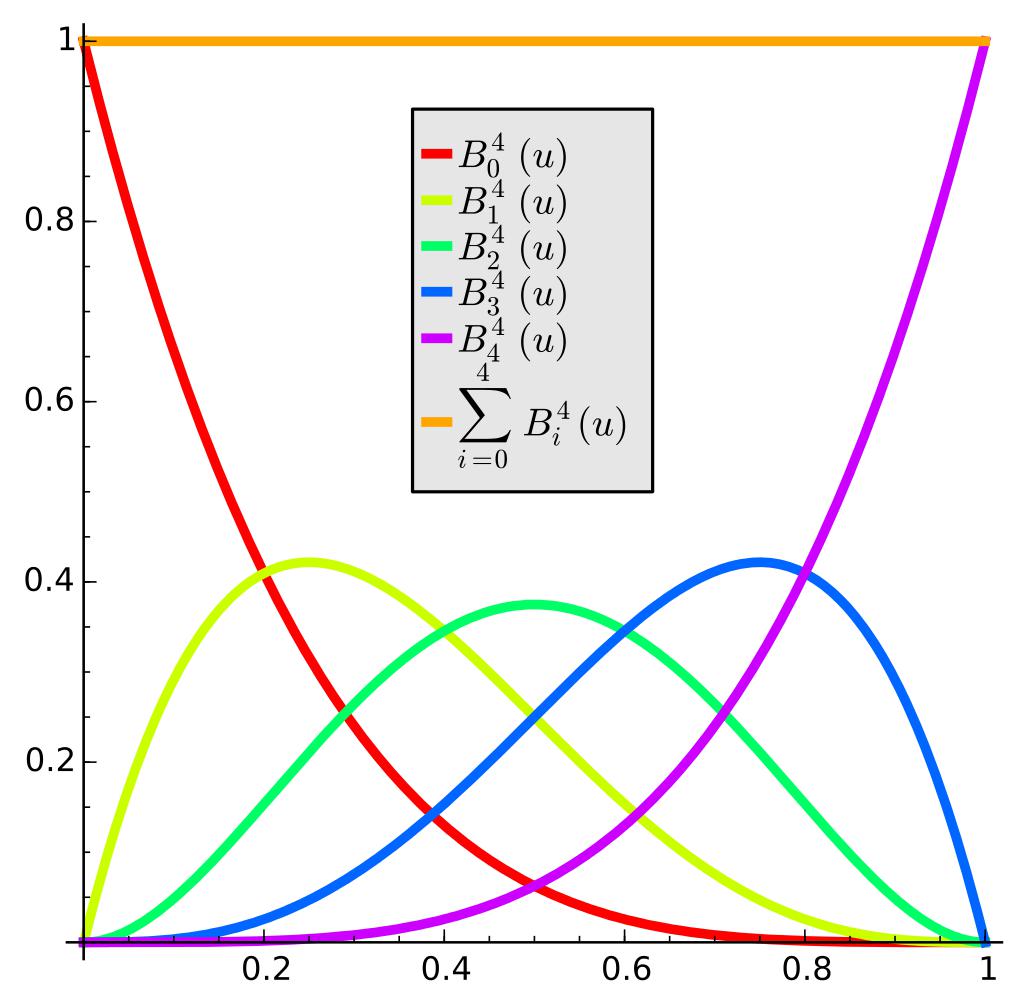
　　n階Bernstein基礎多項式的表達形式為：

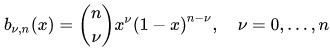
例如：。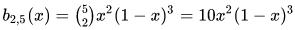

　　Bernstein基礎多項式的一個重要性質是其所有項之和為1：

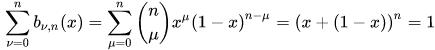
　　n階Bernstein基礎多項式可以組成一個多項式向量空間Π_n，那麼空間中任意一點可以表示成Bernstein基礎多項式的線性組合：

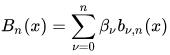
其中β_v為Bernstein係數或Bézier係數，其實上面的表達式就是Bézier曲線的表達式。