print( “Hello，NumPy！” )

2020 年 11 月 8 日
筆記
numpy, Python

print( “Hello，NumPy！” )

學習痛苦啊，今天學，明天丟。這種天氣，還是睡覺最舒服了。

咱說歸說，鬧歸鬧，但還是得學才行啊。

之前在學習的過程中一直都有記錄筆記的習慣，但筆記品質可不敢恭維，大多都未曾整理，不過拿來複習倒是個不錯的選擇。

自打接觸Python以來，寫的最多的就是爬蟲了，什麼網路小說啊，虛擬遊戲幣啊，考試題庫啊之類的都有寫過，也幫別人爬過不少網站公開數據。之前也整理過一篇爬蟲相關的文章（太懶了，才一篇，之後有機會有時間，再整理出來吧）：網路爬蟲之頁面花式解析

再之後的話，就對Social Engineering產生了一定的興趣，或許需要能言善辯，巧舌如簧，達到「江湖騙子」的等級，才能玩轉社會工程學吧。之前也寫過一篇Web滲透相關的文章：Taoye滲透到一家黑平台總部，背後的真相細思極恐。

這裡還是有必要提醒一下大家，對於一些不信任的人或資訊，如果你會一些網路安全相關技能，可以當做一次滲透經驗，否則的話，最好的處理方式是置之不理，別讓你的好奇心成為墜入深淵的開始，尤其是在這雲龍混雜的虛擬網路世界中。就在前幾天，警方還破獲了全國最大網路 luo liao 敲詐案呢，受害者達10餘萬人，涉案金額也有XXXXXXXXXXXXXXX，大家還是需要注意的。

反正，學的東西很多、很雜，學的也不精，記錄的筆記也很少回過頭複習。工欲善其事，必先利其器，這不開始系統性學習機器學習么，所以想把之前記錄的Numpy、Pandas、Matplotlib「三劍客」筆記重新整理一下，也算是做一個回顧。

後期的話，會學習一些機器學習演算法，主要參考《機器學習實戰 / Machine Learning in Action》和周志華老師的《機器學習》西瓜書，以及其他一些圈內大佬寫的一些技術文章。能手撕的話盡量手撕，不能手撕只能說明自己還有待提高吧。

Flag立的太多，感覺會被啪啪打臉。沒事，慢慢來吧，打臉也不怕，反正皮糙肉厚 (￣_,￣ )

這篇文章先把NumPy整理出來吧，可能記錄的並不全面，只記錄了一些常用的，其他的話後期用到了再進行更新吧。以下內容主要參考菜鳥教程和NumPy官方文檔：

NumPy菜鳥教程：//www.runoob.com/numpy/numpy-tutorial.html
NumPy官方文檔：//numpy.org/doc/stable/user/quickstart.html

關於NumPy的安裝，前面在介紹深度學習環境搭建的時候已經介紹過了，推薦安裝Anaconda，其內部集成了大量第三方工具模組，而不需要手動 pip install ...，這一點就有點像Java中的Maven。Anaconda可參考：基於Ubuntu+Python+Tensorflow+Jupyter notebook搭建深度學習環境

如果您沒有安裝Anaconda那也沒事，只需要在Python環境下執行以下命令安裝NumPy即可：

> pip3 install numpy -i //pypi.tuna.tsinghua.edu.cn/simple

以下內容採用的NumPy的版本為：1.18.1

In [1]: import numpy as np

In [2]: np.__version__
Out[2]: '1.18.1'

在NumPy中，操作的對象大多為ndarray類型，也可稱其別名為array，我們可以把它看做矩陣或向量。

創建np.ndarray對象有多種方式，NumPy中也有多個api可供調用，比如我們可以通過如下方式創建一個指定的ndarray對象：

In [7]: temp_array = np.array([[1, 2, 3], [4, 5, 6]], dtype = np.int32)

In [8]: temp_array
Out[8]:
array([[1, 2, 3],
       [4, 5, 6]])

In [9]: type(temp_array)
Out[9]: numpy.ndarray       # 輸出的類型為ndarray

當然了，也可以調用arange，然後對其進行reshape操作來改變其形狀，將向量轉換成2×3的矩陣形式，此時的對象類型依然是numpy.ndarray：

In [14]: temp_array = np.arange(1, 7).reshape(2, 3)     # arange產生向量，reshape改變形狀，轉化成矩陣

In [15]: temp_array
Out[15]:
array([[1, 2, 3],
       [4, 5, 6]])

In [16]: type(temp_array)       # 輸出的類型依然是ndarray
Out[16]: numpy.ndarray

由上，我們可以發現，無論通過什麼方式（其他方式後期會有介紹）來創建對象，NumPy操作的都是ndarray類型，且該類型對象中主要包含以下屬性：

ndarray.ndim：表示ndarray的軸數，也可理解成維度，或者可以通俗的理解成外層中括弧的數量。比如[1, 2, 3]的ndim就是1，[[1], [2], [3]]的ndim等於2，[[[1]], [[2]], [[3]]]的ndim等於3（注意觀察外層中括弧的數量）
ndarray.shape：表示ndarray的形狀，輸出的是一個元組。該ndarray有n行m列，那輸出的就是(n, m)，比如[[1], [2], [3]]輸出的是(3, 1)，[[[1]], [[2]], [[3]]]輸出的是(3, 1, 1)，[[[1, 2]], [[3, 4]]]輸出的是(2, 1, 2)。通過上述3個例子，可以發現shape是按照從外至內的順序來表示的
ndarray.size：這個比較容易理解，表示的就是ndarray內部元素的總個數，也就是shape的乘積
ndarray.dtype：表示ndarray內部元素的數據類型，常見的有numpy.int32、numpy.int64、numpy.float32、numpy.float64等

以上就是ndarray中常見的一些屬性，注意：只是部分，並非全部，其他屬性可參考官方文檔

我們可以通過以下列子來觀察下ndarray的各個屬性，以及其內部的屬性應該如何修改：

以上例子中涉及到的np.expand_dims和np.astype會在後面進行介紹。

np.zeros可以創建一個元素全0的ndarray，np.ones則可以創建一個元素全1的ndarray。創建的時候可以指定ndarray的shape形狀，也可以通過dtype屬性指定內部元素的數據類型：

In [70]: np.zeros([2,3,2], dtype=np.float32)
Out[70]:
array([[[0., 0.],
        [0., 0.],
        [0., 0.]],

       [[0., 0.],
        [0., 0.],
        [0., 0.]]], dtype=float32)

In [71]: np.ones([3,2,2], dtype=np.float32)
Out[71]:
array([[[1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.]],

       [[1., 1.],
        [1., 1.]]], dtype=float32)

另外，在Tensorflow中可以通過tf.fill產生指定元素的指定shape張量，如下產生2×3的張量，且內部元素為100：

In [76]: import tensorflow as tf

In [77]: tf.fill([2,3], 100)
Out[77]:
<tf.Tensor: shape=(2, 3), dtype=int32, numpy=
array([[100, 100, 100],
       [100, 100, 100]])>

而在NumPy中，也有fill介面，只不過只能通過已有的ndarray才能調用fill，而無法直接np.fill進行調用：

In [79]: data = np.zeros([2, 3])

In [80]: data.fill(100)

In [81]: data
Out[81]:
array([[100., 100., 100.],
       [100., 100., 100.]])

np.arange與常用的range作用類似，用於產生一個固定區間連續的ndarray，注意取左不取右，且數組之間成一個等差數列，公差可自行定義（可為小數），如下：

In [85]: np.arange(10)
Out[85]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

In [86]: np.arange(3, 10, 2)
Out[86]: array([3, 5, 7, 9])

In [87]: np.arange(3, 10, 0.7)
Out[87]: array([3. , 3.7, 4.4, 5.1, 5.8, 6.5, 7.2, 7.9, 8.6, 9.3])

numpy.linspace 函數用於創建一個一維數組，數組是一個等差數列構成的，可以指定元素內部元素的個數以及是否包含stop值。如下，在區間1-5中創建一個元素數目為10的等差數列：

In [89]: np.linspace(1, 5, 10)      # 默認包含stop
Out[89]:
array([1.        , 1.44444444, 1.88888889, 2.33333333, 2.77777778,
       3.22222222, 3.66666667, 4.11111111, 4.55555556, 5.        ])

In [90]: np.linspace(1, 5, 10, endpoint = False)    # endpoint屬性可以設置不包含stop
Out[90]: array([1. , 1.4, 1.8, 2.2, 2.6, 3. , 3.4, 3.8, 4.2, 4.6])

np.random.random和np.random.rand隨機從0-1中生成對應shape的ndarray對象：

In [4]: np.random.random([3, 2])
Out[4]:
array([[0.68755531, 0.56727707],
       [0.86027161, 0.01362836],
       [0.56557302, 0.94283249]])

In [5]: np.random.rand(2, 3)
Out[5]:
array([[0.19894754, 0.8568503 , 0.35165264],
       [0.75464769, 0.29596171, 0.88393648]])

np.random.randint隨機生成指定範圍的ndarray，且內部元素為int類型：

In [6]: np.random.randint(0, 10, [2, 3])
Out[6]:
array([[0, 6, 9],
       [5, 9, 1]])

np.random.randn返回滿足標準正態分布的ndarray（均值為0，方差為1）：

In [7]: np.random.randn(2,3)
Out[7]:
array([[ 2.46765106, -1.50832149,  0.62060066],
       [-1.04513254, -0.79800882,  1.98508459]])

另外，我們在NumPy中使用random的時候，都是隨機產生的一組數據，而要想每次產生的數據相同，則需要通過np.random.seed來進行設置：

In [33]: np.random.seed(100)

In [34]: np.random.randn(2, 3)
Out[34]:
array([[-1.74976547,  0.3426804 ,  1.1530358 ],
       [-0.25243604,  0.98132079,  0.51421884]])

In [35]: np.random.seed(100)

In [36]: np.random.randn(2, 3)
Out[36]:
array([[-1.74976547,  0.3426804 ,  1.1530358 ],
       [-0.25243604,  0.98132079,  0.51421884]])

在NumPy中的一維ndarray里，就如同列表一樣操作，可以對其進行切片和遍歷等操作：

In [5]: a
Out[5]: array([1., 2., 3., 4., 5., 6., 7., 8., 9.])

In [6]: a[2], a[2:5]
Out[6]: (3.0, array([3., 4., 5.]))

In [7]: a * 3, a ** 3   # 立方
Out[7]:
(array([ 3.,  6.,  9., 12., 15., 18., 21., 24., 27.]),
 array([  1.,   8.,  27.,  64., 125., 216., 343., 512., 729.]))
 
In [13]: for i in a:
...:     print(i, end=", ")
1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0,

假如我們的ndarray並非是一維數組，而是二維矩陣，或是更高維度的ndarray，則我們需要對其進行多維度的切分。且當我們對高維度的ndarray進行遍歷的時候，則遍歷出單個結果的維度比元維度少一，比如2維矩陣遍歷得到的結果為1維向量，三維遍歷的結果為2維矩陣。

另外，還有一點需要說明的是，加入我的數據的維度相當高，為了方便我們對數據進行索引，NumPy為我們提供了...的方式來進行切分，具體例子如下：

In [14]: a = np.random.randint(0, 2, 6).reshape(2, 3)

In [15]: a
Out[15]:
array([[1, 1, 1],
       [1, 0, 1]])

In [16]: a[:, :2]
Out[16]:
array([[1, 1],
       [1, 0]])

In [17]: for i in a:        # 對矩陣進行遍歷，則輸出的是行向量，單個輸出的維度比原維度少1
    ...:     print(i, end=", ")
[1 1 1], [1 0 1],

In [19]: data = np.random.randint(0, 2, [2, 2, 3])

In [20]: data
Out[20]:
array([[[0, 0, 1],
        [0, 1, 1]],

       [[1, 0, 0],
        [0, 1, 0]]])

In [21]: data[..., :2]      # ...則表示前兩個維度全要，相當於 data[:, :, :2]
Out[21]:
array([[[0, 0],
        [0, 1]],

       [[1, 0],
        [0, 1]]])

shape操作：

a.ravel()、ndarray.flatten()，將ndarray進行拉伸操作（拉直成向量形式）
a.reshape()，重新改變a的shape外形
a.T、a.transpose()，返回a的倒置矩陣

以上幾個操作返回的都是新的結果，而不改變原來的ndarray（a）。且上述操作默認的都是橫向操作，如果需要縱向，則需要控制order參數，具體操作可參考菜鳥教程。除了reshape之外，還有resize，只不過resize會改變a的結果，而並非產生一個新的結果：

還有一個小技巧需要掌握的是，在進行reshape的時候，假如傳入-1，則會自動計算出對應的結果。比如一個 2×3的矩陣a，我們進行a.reshape(3, -1)，則這裡的-1代表的就是2，當我們數據量大的時候，這個用起來還是挺方便的：

In [44]: a
Out[44]:
array([[1, 1, 1],
       [1, 0, 1]])

In [45]: a.reshape([3, -1])
Out[45]:
array([[1, 1],
       [1, 1],
       [0, 1]])

數組維度的修改：

維度	描述
broadcast_to	將數組廣播到新形狀
expand_dims	擴展數組的形狀
squeeze	從數組的形狀中刪除一維條目

具體操作如下：

數組的連接：

函數	描述
concatenate	連接沿現有軸的數組序列
hstack	水平堆疊序列中的數組（列方向）
vstack	豎直堆疊序列中的數組（行方向）

下面程式碼顯示了數組連接的操作，其中concatenate可以通過控制axis的值來確定連接的方向，作用等同於hstack和vstack。還有一點需要注意的是：以下示例僅僅是連接兩個數組，其實可以同時連接多個的，比如np.concatenate((x, y, z), axis=1)

數組的切分：

函數	描述
split	將一個數組分割為多個子數組
hsplit	將一個數組水平分割為多個子數組（按列）
vsplit	將一個數組垂直分割為多個子數組（按行）

同數組的連接一樣，split可以通過控制axis屬性來得到與hsplit、vsplit相同的作用，下面只給出split的示例，關於hsplit和vsplit可參考官方文檔：

數組元素的添加和刪除：

函數	描述
append	將值添加到數組末尾
insert	沿指定軸將值插入到指定下標之前
delete	刪掉某個軸的子數組，並返回刪除後的新數組

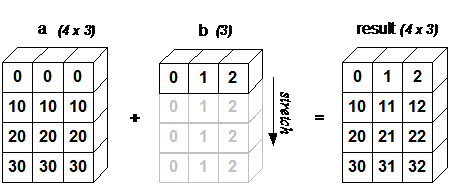
廣播(Broadcast)是 numpy 對不同形狀(shape)的數組進行數值計算的方式，對數組的算術運算通常在相應的元素上進行。

如果兩個數組 a 和 b 形狀相同，即滿足 a.shape == b.shape，那麼 a*b 的結果就是 a 與 b 數組對應位相乘。這要求維數相同，且各維度的長度相同。

In [8]: import numpy as np

In [9]: a = np.array([1,2,3,4])
   ...: b = np.array([10,20,30,40])

In [10]: a * b
Out[10]: array([ 10,  40,  90, 160])

當運算中的 2 個數組的形狀不同時，numpy 將自動觸發廣播機制。如：

In [11]: a = np.array([[ 0, 0, 0],
    ...:            [10,10,10],
    ...:            [20,20,20],
    ...:            [30,30,30]])
    ...: b = np.array([1,2,3])

In [12]: a + b
Out[12]:
array([[ 1,  2,  3],
       [11, 12, 13],
       [21, 22, 23],
       [31, 32, 33]])

下面的圖片展示了數組 b 如何通過廣播來與數組 a 兼容。

np.tile可以對目標操作數組進行廣播擴展，比如 1×3 如下操作可以廣播為 4×6，注意與前面所說的broadcast_to進行區別，broadcast_to必須要擴維，而tile可擴維，也可不擴維，具體操作根據自己的實際需求進行。

有過Tensorflow經驗的讀者應該知道，其內部也有tile和broadcast操作，但是當我們的數據量比較大的時候，據說tile的效率比broadcast要低，暫時還沒了解原因，以後有用到在了解吧。

In [20]: a
Out[20]: array([[1, 1, 0]])

In [21]: np.tile(a, [4, 2])     # 第二個參數表示各個維度廣播的倍數，這裡表示的是行擴4倍，列擴2倍
Out[21]:
array([[1, 1, 0, 1, 1, 0],
       [1, 1, 0, 1, 1, 0],
       [1, 1, 0, 1, 1, 0],
       [1, 1, 0, 1, 1, 0]])

關於NumPy中的複製和試圖：這個部分的知識也是我之前在學習NumPy時候所遺漏的點，趁著這個機會，把它在這記錄一下。

沒有複製

關於這一點，其實在之前記錄LeetCode 熱題 HOT 100（01，兩數相加）演算法的時候同樣提到過，這一點還是需要格外注意的。

視圖或者淺拷貝（view）

同樣採用上面一樣的程式碼，僅僅修改了第57行，將 y = x 和 y = x.view()，可以發現，此時的x和y的id值不一樣，也就是說他們的記憶體地址不一樣，我們修改x的shape之後，y的shape並沒有發生改變。

但是，當我們改變不是shape，而是改一個變數組內部的數據，則另一個數組同樣會發生改變

副本或者深拷貝(copy)

視圖或者淺拷貝採用的是view，而副本或者深拷貝採用的是copy。使用copy的時候無論是修改一個數組的shape，還是內部元素，另一個數組都不會發生改變。

（關於copy，這裡就不再演示程式碼了，讀者可自行操作，然後進行比較）

最後總結一下：

y = x，說明x和y的記憶體地址相同，修改其中一個，另一個也會隨著發生改變（無論是shape，還是內部元素）
y = x.view()，兩者的記憶體地址不一樣，修改其中一個的shape，另一個不會發生改變；而修改其中一個元組的內部元素，則另外一個會跟著發生改變
y = x.copy()，兩者的記憶體地址不一樣，無論是修改一個元組的shape，還是內部元素，另外一個都不會發生改變，兩者相互獨立

NumPy中的數學相關函數，這部分內容沒什麼好講的：

np.pi，返回π值
np.sin()，返回正弦值
np.cos()，返回餘弦值
np.tan()，返回正切值
numpy.ceil()，返回大於或者等於指定表達式的最小整數，即向上取整。
np.exp(2)，返回指數值，也就是 $e^2$

其他相關數學函數，可參考官方文檔。

NumPy中的算術運算，這部分內容也沒什麼好講的：

numpy.add(a,b)：兩數組相加
numpy.subtract(a,b)：兩數組相減
numpy.multiply(a,b)：兩數組相乘
numpy.divide(a,b)：兩數組相除
numpy.reciprocal(a)，返回倒數
numpy.power(a, 4)，返回a的四次方

NumPy中的統計函數，這個稍微記錄一下：

以上示例了在數組中獲取最值以及最值之差的方式，傳入了axis參數，則按照對應方向獲取，假如沒有傳入axis參數，則表示獲取數組整體的最值。除了以上幾個介面之外，還有其他一些常見的統計函數，具體操作和上述並無一二，如下：

np.amin()：獲取最小值
np.amax()：獲取最大值
np.ptp()：獲取最值之差
np.median()：獲取中位數（中值）
np.mean()：獲取均值
np.var()：獲取方差，$\sigma^2 = \frac{1}{n}\sum_{i=1}^{n(x_i-\overline{x})}2$
np.std()：獲取標準差，$\sigma$

NumPy中的線性代數：

np.dot(a, b) 就是兩個矩陣的乘積
np.vdot(a, b) 兩個矩陣對應位置數的乘積之和
np.inner(a, b) 內積，就是a的每行與b的每行相乘求和

比如a=[[1, 0], [1, 1]]，b=[[1, 2], [1, 3]]
np.inner(a, b)相當於[1, 0] * [1, 2] = 1 -> 為第一個數
[1, 0] * [1, 3] = 1 -> 為第二個數
[1, 1] * [1, 2] = 3 -> 為第三個數
[1, 1] * [1, 3] = 4 -> 為第四個數

矩陣乘積就是第一個矩陣的行與第二個矩陣的列乘積之和，而inner相當於第一個矩陣和第二個矩陣的行乘積之和

np.matmul(a, b) 目前感覺和np.dot(a, b)作用一樣，都是矩陣乘積
np.linalg.det(a) 計算矩陣的行列式的值
np.linalg.solve(a, [[1], [1]]) 求線性方程組的解，第一個的參數相當於係數，第二個參數相當於參數項
np.linalg.inv(a) 計算矩陣的逆矩陣

# 將數組保存到以 .npy 為擴展名的文件中。
numpy.save(file, arr, allow_pickle=True, fix_imports=True)

file：要保存的文件，擴展名為 .npy，如果文件路徑末尾沒有擴展名 .npy，該擴展名會被自動加上。
arr: 要保存的數組
allow_pickle: 可選，布爾值，允許使用 Python pickles 保存對象數組，Python 中的 pickle 用於在保存到磁碟文件或從磁碟文件讀取之前，對對象進行序列化和反序列化。
fix_imports: 可選，為了方便 Pyhton2 中讀取 Python3 保存的數據。

In [81]: a = np.random.randint(1, 10, [3, 4])

In [82]: np.save("a.npy", a)

In [83]: np.load("a.npy")
Out[83]:
array([[2, 7, 3, 1],
       [4, 6, 4, 3],
       [2, 2, 9, 5]])

參考資料：

參考資料：

[1] NumPy菜鳥教程：//www.runoob.com/numpy/numpy-tutorial.html
[2] NumPy官方文檔：//numpy.org/doc/stable/user/quickstart.html

時間不太夠，後面寫的有點倉促了，但應該並不影響正常閱讀和以後的複習，暫時就這樣吧。

注意：只記錄了一些常用的，其他的話後期用到了再進行更新吧，其他內容可自行參考文檔。

本來是打算按照《機器學習實戰 / Machine Learning in Action》這本書來手撕其中程式碼的，但由於實際原因，可能需要先手撕SVM了，這個演算法感覺還是挺讓人頭疼，其中內部太複雜了，也很少有資料將其完整的推導出來，也涉及到了許多陌聲的名詞，如：非線性約束條件下的最優化、KKT條件、拉格朗日對偶、最大間隔、最優下界、核函數等等，天書或許、可能、大概就是這樣的吧。好在之前有學習過SVM，但想必依然需要花費大力氣來手撕，也需要參考不少資料，包括但不局限於《機器學習實戰 / Machine Learning in Action》、《機器學習》、《統計學習方法》。

所以，下期的話，應該會開始手撕SVM，至於最後能不能手撕成功，還真不好說。時間可能需要不少，這期間的LeetCode HOT 100 還需要正常刷起來。

我是Taoye，愛專研，愛分享，熱衷於各種技術，學習之餘喜歡下象棋、聽音樂、聊動漫，希望藉此一畝三分地記錄自己的成長過程以及生活點滴，也希望能結實更多志同道合的圈內朋友，更多內容歡迎來訪微信公主號：玩世不恭的Coder。

Tags: numpy Python