遞歸思想的巧妙理解

邏輯是數學的少年時代，數學是邏輯的成年時代。

——羅素

「遞歸」

這是在程式、演算法設計中的基礎和重中之重。當初理解這一點我也花費了不少時間，對於初學者來說，如何生動形象的展現著一過程，成了理解這一思想的關鍵。

這篇博文的來由，源於同學問我的一個問題：

我一看啊，這波，這波是明顯的遞歸啊！！

我想著，怎麼解釋呢，於是打開百度搜索遞歸：

定義

程式調用自身的編程技巧稱為遞歸（ recursion）。遞歸做為一種演算法在程式設計語言中廣泛應用。一個過程或函數在其定義或說明中有直接或間接調用自身的一種方法，它通常把一個大型複雜的問題層層轉化為一個與原問題相似的規模較小的問題來求解，遞歸策略只需少量的程式就可描述出解題過程所需要的多次重複計算，大大地減少了程式的程式碼量。遞歸的能力在於用有限的語句來定義對象的無限集合。一般來說，遞歸需要有邊界條件、遞歸前進段和遞歸返回段。當邊界條件不滿足時，遞歸前進；當邊界條件滿足時，遞歸返回。

我想這，這麼生硬的解釋，還是別麻煩人家了吧，於是這個解釋就鴿了好幾天

奇思妙想

某個摸魚的晚上，我突然想到了一個解釋遞歸生動形象的例子，那就是：

俄羅斯套娃！！

那麼，如何用俄羅斯套娃的思想去理解遞歸思想呢？

又是眾所周知，遞歸其實就是程式調用自身，這不就好像是，在自己肚子裡面裝了一個自己么？

不過，我們開這個套娃的方式，得遵循以下規則；

先吧套娃的上半部分拿走（執行調用自身的函數上邊的程式碼）；

繼續拿上半部分，直到拿出了一個不能在開的娃（遞歸到底）；

看看這個不能再套娃的娃（完整的執行這個最「深」的函數）；

在依次拿出所有套娃的下半身（自底向上執行所有遞歸函數的下半部分）。

案例解釋

我們先看這個求樹的深度的程式碼：

int TreeDepth(BT *T){
    int ld=0,rd=0;
    if(T==NULL) return 0;
    else{
        ld=TreeDepth(T->lchild);
        rd=TreeDepth(T->rchild);
        if(ld>rd)
            return ld+1;
        else
            return rd+1;
    }
}

我就畫個圖來看看吧

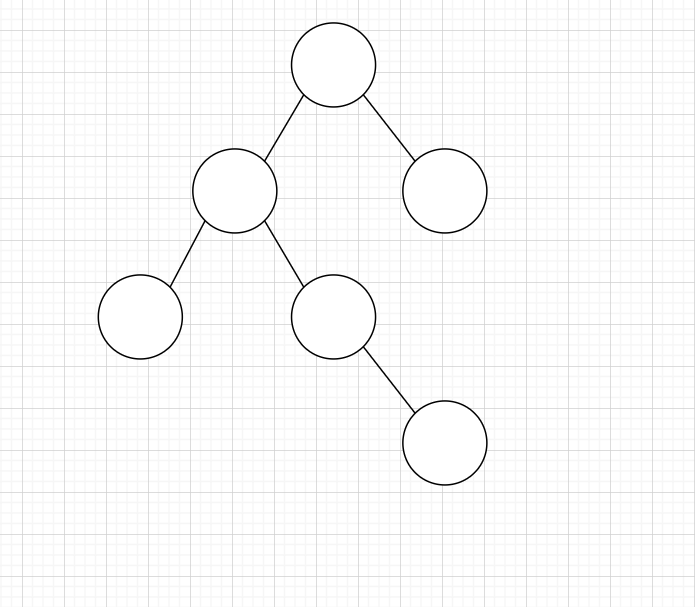
假設有這麼一顆樹，BT是函數中指針*T所在位置

我們執行這一段程式碼

int TreeDepth(BT *T){
    int ld=0,rd=0;
    if(T==NULL) return 0;
    else{
        ld=TreeDepth(T->lchild);

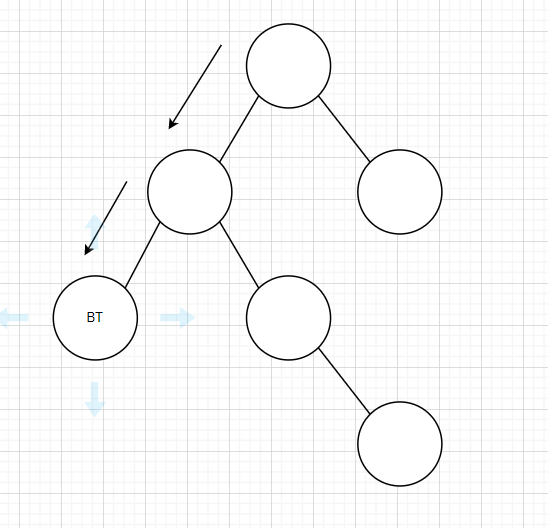
先遞歸到底邊，在走下去，全是NULL了，就可以執行後一段程式碼

if(ld>rd)
            return ld+1;
        else
            return rd+1;

當然，這裡ld和rd都是0，返回值是1，根據

ld=TreeDepth(T->lchild);

則上一層函數的ld=1

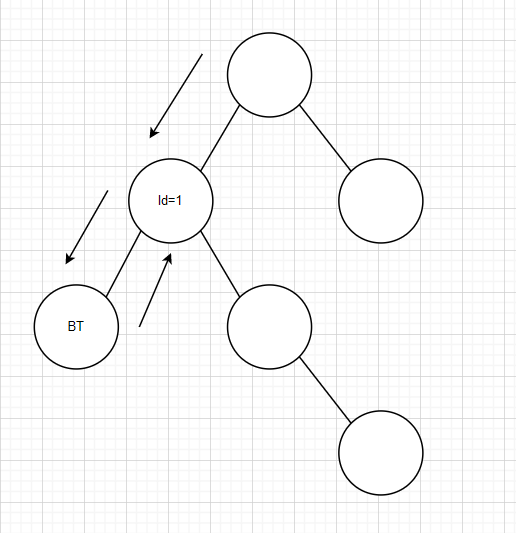
我們繼續看，因為這一個函數已經執行結束了，我們來執行上一個函數的後半段程式碼。

       rd=TreeDepth(T->rchild);
        if(ld>rd)
            return ld+1;
        else
            return rd+1;
    }
}

這裡我們發現，可以一直走右子樹走下去，參考上一步的操作，以此類推，我們得到下圖

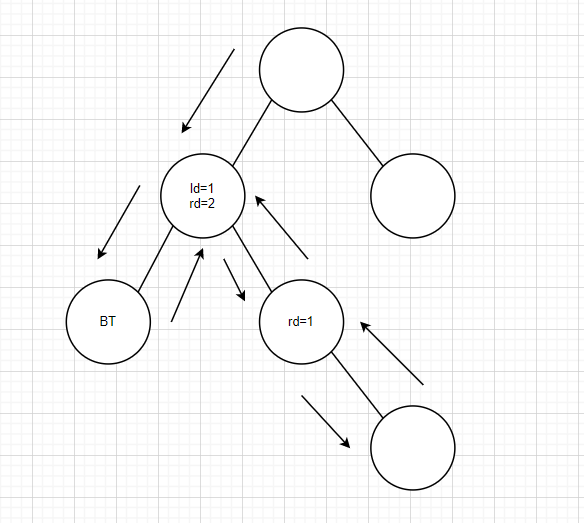
再繼續推下去，整個程式的返回值就一目了然了

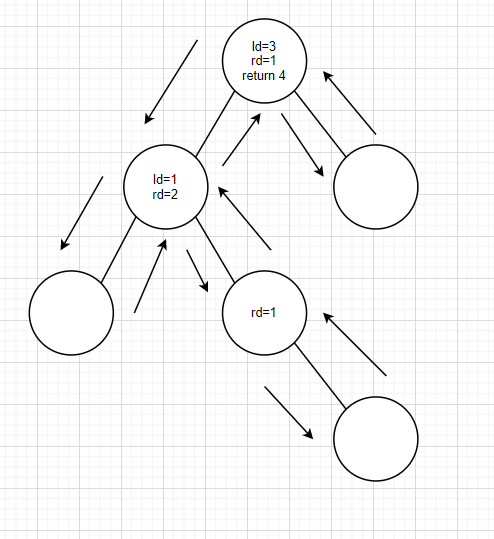
這裡還是要再提一下深度優先搜索（DFS），眾所周知深搜的最基本技巧就是遞歸。

PS：雖然深搜也可以用棧實現，不過遞歸就是程式自己調出棧來儲存數據，差別不大。

樹是特殊的圖，樹的遍歷也是圖的遍歷，這種按照深度一口氣遍歷下來的方式，就是我們所謂的DFS，再樹基礎的學習過程中，我們也可以體會到很多圖的性質

希望我的拋磚引玉能引起更多的思考😄

Tags: 數據結構數據結構與演算法演算法