PCA降維的原理、方法、以及python實現。

• 2019 年 11 月 13 日
• 筆記

PCA(主成分分析法)

1. PCA(最大化方差定義或者最小化投影誤差定義)是一種無監督演算法，也就是我們不需要標籤也能對數據做降維，這就使得其應用範圍更加廣泛了。那麼PCA的核心思想是什麼呢？

• 例如D維變數構成的數據集，PCA的目標是將數據投影到維度為K的子空間中，要求K<D且最大化投影數據的方差。這裡的K值既可以指定，也可以利用主成分的資訊來確定。
• PCA其實就是方差與協方差的運用。
• 降維的優化目標：將一組 N 維向量降為 K 維，其目標是選擇 K 個單位正交基，使得原始數據變換到這組基上後，各變數兩兩間協方差為 0，而變數方差則儘可能大（在正交的約束下，取最大的 K 個方差）。

2. PCA存在的問題：

• 原來的數據中比如包括了年齡，性別，身高等指標降維後的數據既然維度變小了，那麼每一維都是什麼含義呢？這個就很難解釋了，所以PCA本質來說是無法解釋降維後的數據的物理含義，換句話說就是降維完啦電腦能更好的認識這些數據，但是咱們就很難理解了。
• PCA對數據有兩個假設：數據必須是連續數值型；數據中沒有缺失值。
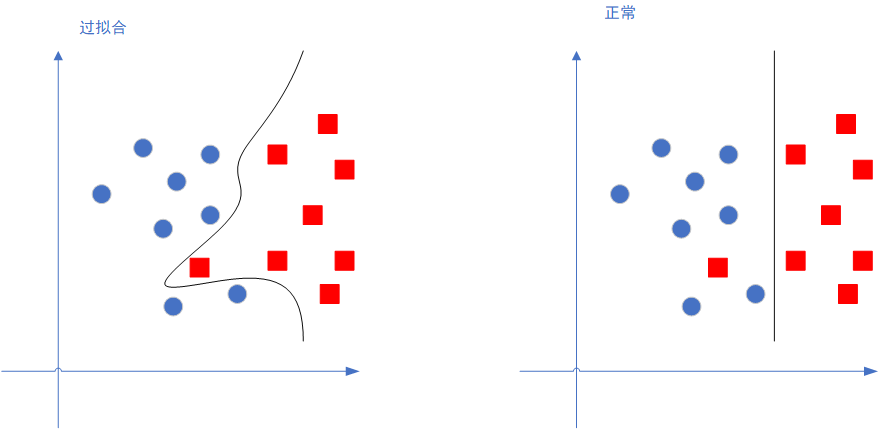
• 過擬合：PCA 保留了主要資訊，但這個主要資訊只是針對訓練集的，而且這個主要資訊未必是重要資訊。有可能捨棄了一些看似無用的資訊，但是這些看似無用的資訊恰好是重要資訊，只是在訓練集上沒有很大的表現，所以 PCA 也可能加劇了過擬合；

3. PCA的作用：

• 緩解維度災難：PCA 演算法通過捨去一部分資訊之後能使得樣本的取樣密度增大（因為維數降低了），這是緩解維度災難的重要手段；
• 降噪：當數據受到雜訊影響時，最小特徵值對應的特徵向量往往與雜訊有關，將它們捨棄能在一定程度上起到降噪的效果；
• 特徵獨立：PCA 不僅將數據壓縮到低維，它也使得降維之後的數據各特徵相互獨立；

4. 方差的作用：咱們可以想像一下，如果一群人都堆疊在一起，我們想區分他們是不是比較困難，但是如果這群人站在馬路兩側，我們就可以很清晰的判斷出來應該這是兩伙人。所以基於方差我們可以做的就是讓方差來去判斷咱們數據的擁擠程度，在這裡我們認為方差大的應該辨識度更高一些，因為分的比較開（一條馬路給隔開啦）。方差可以度量數值型數據的離散程度，數據若是想要區分開來，他那他們的離散程度就需要比較大，也就是方差比較大。

5. 協方差的作用：

6. 計算過程：(下圖為採用特徵值分解的計算過程，若採用SVM演算法，則無需計算協方差矩陣！)

為什麼我們需要協方差矩陣？我們最主要的目的是希望能把方差和協方差統一到一個矩陣里，方便後面的計算。

　　假設我們只有 a 和 b 兩個變數，那麼我們將它們按行組成矩陣 X：(與matlab不同的是，在numpy中每一列表示每個樣本的數據，每一行表示一個變數。比如矩陣X，該矩陣表示的意義為：有m個樣本點，每個樣本點由兩個變數組成！）

　　然後：

　　我們可以看到這個矩陣對角線上的分別是兩個變數的方差，而其它元素是 a 和 b 的協方差。兩者被統一到了一個矩陣里。

7. 特徵值與特徵向量的計算方法—--特徵值分解與奇異值分解法(SVD)(有關特徵值與奇異值可見我的博文！)

(1) 特徵值分解的求解過程較為簡單，以下圖為例子

(2) 特徵值分解存在的缺點：

• 特徵值分解中要求協方差矩陣A必須是方陣，即規模必須為n*n。
• 後期計算最小投影維度K時，計算量過大。
• 當樣本維度很高時，協方差矩陣計算太慢；

(3) SVD演算法(奇異值分解)的提出克服這些缺點，目前幾乎所有封裝好的PCA演算法內部採用的都是SVD演算法進行特徵值、特徵向量以及K值的求解。

• 奇異值(每個矩陣都有)：設A是一個mXn矩陣，稱正半定矩陣A‘A的特徵值的非負平方根為矩陣A的奇異值，其中A‘表示矩陣A的共扼轉置矩陣(實數矩陣的共軛轉置矩陣就是轉置矩陣，複數矩陣的共軛轉置矩陣就是上面所說的行列互換後每個元素取共軛)
• 只有方陣才有特徵值。

(4) SVD演算法的計算過程：(numpy中已經將SVD進行了封裝，所以只需要調用即可)

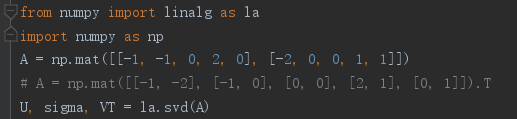
可以發現，採用SVD演算法無需計算協方差矩陣，這樣在數據量非常大的時候可以降低消耗。

• A為數據矩陣，大小為M*N(2*5)
• U是一個由與數據點之間具有最小投影誤差的方向向量所構成的矩陣，大小為M*M(2*2),假如想要將數據由M維降至K維，只需要從矩陣U中選擇前K個列向量，得到一個M*K的矩陣，記為Ureduce。按照下面的公式即可計算降維後的新數據：降維後的數據矩陣G = A.T * Ureduce. 
• sigma為一個列向量，其包含的值為矩陣A的奇異值。
• VT是一個大小為N*N的矩陣，具體意義我們無需了解。

利用python實現PCA降維(採用SVD的方法)：

 1 from numpy import linalg as la   2 import numpy as np   3 #1.矩陣A每個變數的均值都為0，所以不用進行“去平均值”處理。倘若矩陣A的每個變數的均值不為0，則首先需要對數據進行預處理   4 #  才可以進行協方差矩陣的求解。   5 #2.與matlab不同的是，在numpy中每一列表示每個樣本的數據，每一行表示一個變數。   6 #  比如矩陣A，該矩陣表示的意義為：有5個樣本點，每個樣本點由兩個變數組成！   7 #3.np.mat()函數中矩陣的乘積可以使用 * 或 .dot()函數   8 #  array()函數中矩陣的乘積只能使用 .dot()函數。而星號乘（*）則表示矩陣對應位置元素相乘，與numpy.multiply()函數結果相同。   9 A = np.mat([[-1, -1, 0, 2, 0], [-2, 0, 0, 1, 1]])  10 # A = np.mat([[-1, -2], [-1, 0], [0, 0], [2, 1], [0, 1]]).T  11 U, sigma, VT = la.svd(A)  12 print("U:")  13 print(U)  14 print("sigma:")  15 print(sigma)  16 print("VT:")  17 print(VT)  18 print("-"*30)  19 print("降維前的數據：")  20 print(A.T)  21 print("降維後的數據:")  22 print(A.T * U[:,0])

運行結果圖：與上文採用特徵值分解所得到的降維結果一致！

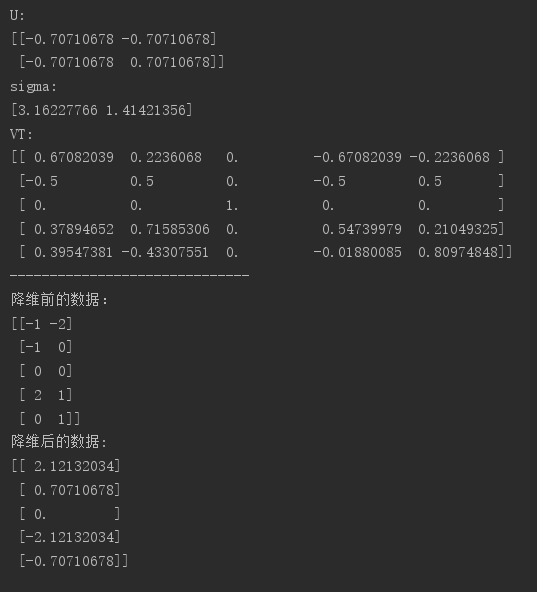
8.PCA的重建

 眾所周知，PCA可以將高維數據壓縮為較少維度的數據，由於維度有所減少，所以PCA屬於有損壓縮，也就是，壓縮後的數據沒有保持原來數據的全部資訊，根據壓縮數據無法重建原本的高維數據，但是可以看作原本高維數據的一種近似。

 還原的近似數據矩陣Q = 降維後的矩陣G * Ureduce.T

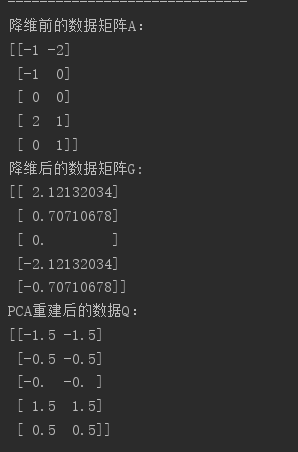
9.採用sklearn封裝好的PCA實現數據降維(採用的是SVD演算法)：

 1 import numpy as np   2 from sklearn.decomposition import PCA   3 # 利用sklearn進行PCA降維處理的時候，數據矩陣A的行數表示數據的個數，數據矩陣A的列數表示每條數據的維度。這與numpy中是相反的！   4 # A = np.mat([[-1, -1, 0, 2, 0], [-2, 0, 0, 1, 1]]).T   5 A = np.mat([[-1, -2], [-1, 0], [0, 0], [2, 1], [0, 1]])   6 pca = PCA(n_components = 1)   7 pca.fit(A)   8 # 投影后的特徵維度的方差比例   9 print(pca.explained_variance_ratio_)  10 # 投影后的特徵維度的方差  11 print(pca.explained_variance_)  12 print(pca.transform(A))

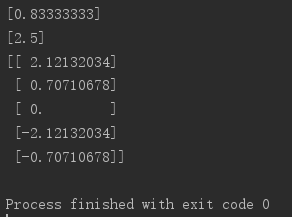
 可以發現，採用sklearn封裝的方法實現PCA與上文的方法達到的結果一致！

10.如何確定主成分數量(針對於Sklearn封裝的PCA方法而言)

PCA演算法將D維數據降至K維，顯然K是需要選擇的參數，表示要保持資訊的主成分數量。我們希望能夠找到一個K值，既能大幅降低維度，又能最大限度地保持原有數據內部的結構資訊。實現的過程是通過SVD方法得到的S矩陣進行操作求解，

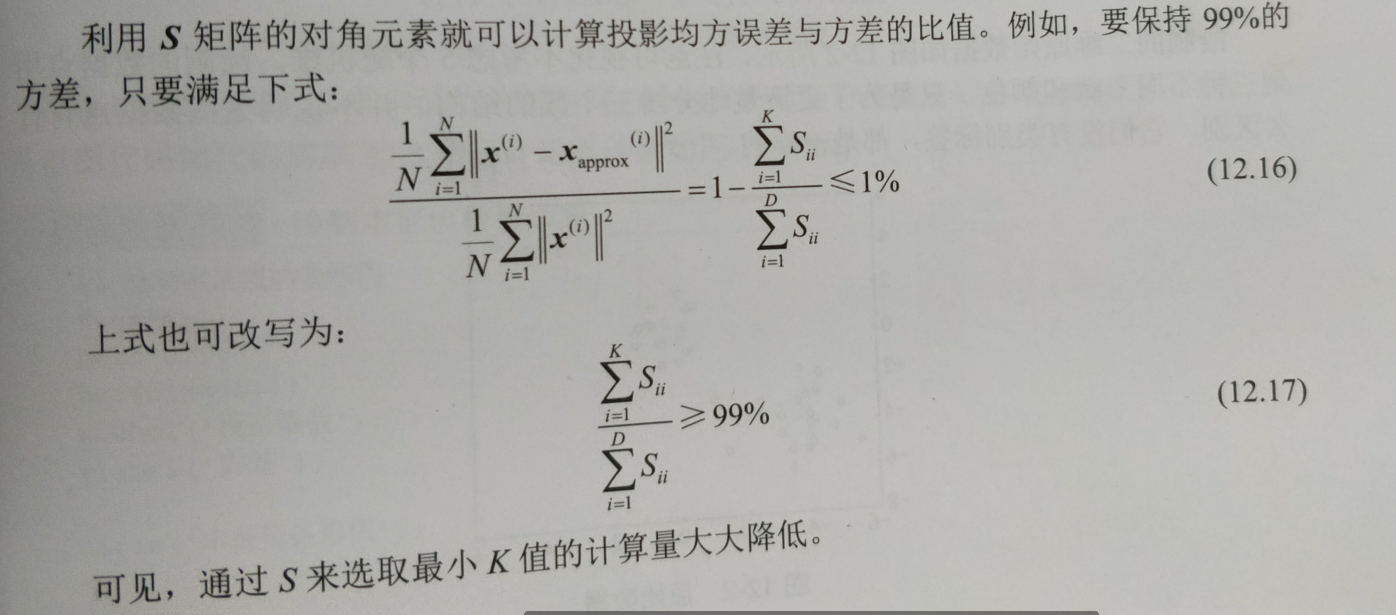
11.sklearn中封裝的PCA方法的使用介紹。

PCA的函數原型

 (1)主要參數介紹

n_components

• 這個參數類型有int型，float型，string型，默認為None。 它的作用是指定PCA降維後的特徵數(也就是降維後的維度)。 
• 若取默認(None)，則n_components==min(n_samples, n_features)，即降維後特徵數取樣本數和原有特徵數之間較小的那個；
• 若n_components}設置為‘mle’並且svd_solver設置為‘full’則使用MLE演算法根據特徵的方差分布自動去選擇一定數量的主成分特徵來降維； 
• 若0<n_components<1，則n_components的值為主成分方差的閾值； 通過設置該變數，即可調整主成分數量K。
• 若n_components≥1，則降維後的特徵數為n_components； 

copy

•  bool (default True) 
• 在運行演算法時，將原始訓練數據複製一份。參數為bool型，默認是True，傳給fit的原始訓練數據X不會被覆蓋；若為False，則傳給fit後，原始訓練數據X會被覆蓋。 

whiten

• bool, optional (default False)
• 是否對降維後的數據的每個特徵進行歸一化。參數為bool型，默認是False。

（2）主要方法介紹：

fit(X,y=None) ：用訓練數據X訓練模型，由於PCA是無監督降維，因此y=None。 

transform(X,y=None) ：對X進行降維。 

fit_transform(X) ：用訓練數據X訓練模型，並對X進行降維。相當於先用fit(X)，再用transform(X)。 

inverse_transform(X) ：將降維後的數據轉換成原始數據。(PCA的重建)

 （3）主要屬性介紹：

components：array, shape (n_components, n_features) ，降維後各主成分方向，並按照各主成分的方差值大小排序。 

explained_variance：array, shape (n_components,) ，降維後各主成分的方差值，方差值越大，越主要。 

explained_variance_ratio：array, shape (n_components,) ，降維後的各主成分的方差值佔總方差值的比例，比例越大，則越主要。 

singular_values：array, shape (n_components,) ，奇異值分解得到的前n_components個最大的奇異值。

參考資料：https://zhuanlan.zhihu.com/p/77151308?utm_source=qq&utm_medium=social&utm_oi=1095998405318430720