Codeforces Round #678 (Div. 2)

Codeforces Round #678 (Div. 2)

A. Reorder

題意：有一個有 n 個數的序列 a ，以及一個數 m ，問能否給序列a重新排序，能夠滿足式子 $\sum_{i=1}^{n}\sum_{j=1}^{n}\frac{a_{j}}{j}=m$。

思路：稍微計算一下便可以發現$1\times \frac{a_{1}}{1}+2\times \frac{a_{2}}{2}+…+n\times \frac{a_{n}}{n}=a_{1}+a_{2}+…+a_{n}$，其實這道題就是問序列的所有數之和是否為m。

程式碼：

#include<bits/stdc++.h>
using namespace std;
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t;
    cin>>t;
    while(t--){
        int n,m,ans=0,get_num;
        cin>>n>>m;
        while(n--){
            cin>>get_num;
            ans+=get_num;
        }
        if(ans==m) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

View Code

B. Prime Square

題意：t 組數據，每組數據給一個 n ，構造一個以 n 為邊長的數字方陣，要求每個數都不能是質數，但是每行每列之和都為質數。

思路：構造，對於每一個 n ，可以考慮從 n 開始往上找質數，每找到一個質數 p 嘗試構造一次，構造方法為主對角線元素為$p-n+1$，其餘位置上的元素均為1，這樣如果$p-n+1$不是質數，那就可以保證滿足題意。（因為每個$p-n+1$都在主對角線上，所以每個$p-n+1$只對當前行列造成影響，所以這樣構造可以保證每一行每一列的和都為我們找到的質數 p ）。

程式碼：

#include<bits/stdc++.h>
using namespace std;
bool is_prime(int n){
    if(n==1) return false;
    for(int i=2;i*i<=n;i++){
        if(n%i==0) return false;
    }
    return true;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int t,n;
    cin>>t;
    while(t--){
        cin>>n;
        int p=n;
        while(!(is_prime(p) && !is_prime(p-n+1))) p++;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(i==j) cout<<p-n+1<<" ";
                else cout<<1<<" ";
            }
            cout<<endl;
        }
        cout<<endl;
    }
    return 0;
}

View Code

C. Binary Search

題意：有一個序列有 n 個數，如果序列有序，則按照如下程式碼可以找到 pos 位置上的數字 x ，現在詢問如果序列無序，而且仍然可以用下面這段程式碼找到位於pos 位置上的數字 x ，請問這樣的序列有多少種，答案對1e9+7取模。

思路：按照程式碼我們可以得知，算至pos的路徑是固定的，而且對於每次循環 left 和 right 所產生的 middle ，我們都可以用來確定 a[middle] 和 x 的大小關係，那麼我們就可以確定某些位置的數字是嚴格大於 x 的，某些位置的數字是嚴格小於 x 的，這樣我們就可以用全排列和乘法原理算出答案。

我們可以來進行二分，當 middle > pos 時，a[middle]是大於 x 的 , 大於 x 的計數變數加一；當middle < pos 時，a[middle]是小於 x 的，小於x的計數變數加一；二分完成後，會剩下$n-big-small$個位置上的數無法確定。所以答案就是從$n-x$個大於 x 的數選 big 個數的全排列乘以從$x-1$個小於 x 的數選 small 個數的全排列乘以剩下$n-big-small-1$個數的全排列，即$A_{n-x}^{big}\times A_{x-1}^{small}\times A_{n-big-small}^{n-big-small}$。當然，如果big>n-x或者small>x-1的話，不存在這樣的排列，答案為0。

程式碼：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod=1e9+7;

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    long long n,x,pos,l,r,big=0,small=0,ans=1;
    cin>>n>>x>>pos;
    l=0;r=n;
    while(l<r){
        long long mid=(l+r)/2;
        if(mid==pos){
            l=mid+1;
        }else if(mid>pos){
            r=mid;
            big++;
        }else if(mid<pos){
            l=mid+1;
            small++;
        }
    }
    if(small>=x || big>n-x){
        cout<<0<<endl;
    }else{
        for(ll i=x-1,j=1;j<=small;i--,j++){
            ans=(ans*i)%mod;
        }
        for(ll i=n-x,j=1;j<=big;i--,j++){
            ans=(ans*i)%mod;
        }
        for(ll i=1;i<=n-small-big-1;i++){
            ans=(ans*i)%mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}

View Code

D. Bandit in a City

題意：城市有 n 個區域編號為1…n，n-1 個單向通路，而且1號區域為主區域，保證主區域可以到達任何其它區域。現在給出 i 號區域有 ai 個人，且一夥土匪位於主區域，他們希望抓住更多的人，他們會一隻往前走，直至最後的區域沒有通往其它區域的路，市民則可以選擇通路進行逃跑，當沒有通往其它區域的路且土匪位於該區域時市民會被抓住。現在土匪想要抓住儘可能多的人，而市民則希望儘可能少的人被抓住，兩方都採取最優解。問土匪最多能抓到多少人。

思路：對於某一個區域，我們考慮當前區域時，土匪最多能抓多少人 ，那麼這個問題依賴於該區域可以通往的其它區域所計算的結果。所以這個問題我們可以拆成一個一個的子問題然後用遞歸的思想來解決。對於任意一個區域 x ，我們需要算出這個當前區域以及這個區域能達到的區域的總人數num，當前區域之後的分支線路數lu，以及人數最多的那條路的人數maxx（這個maxx是考慮到位於尾節點的人無法逃跑），將這三個值放入一個結構體中遞歸時返回。

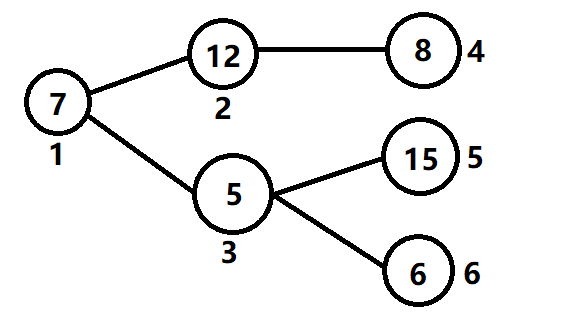
舉個例子，對於上圖這個例子考慮節點1就需要節點2和節點3的值，2需要4的值，3需要5和6的值。對於4節點{num=8,lu=1,maxx=8}，對於5節點{num=15,lu=1,maxx=15}，對於6節點{num=6,lu=1,maxx=6}，對於3節點，這時我們計算的{num=當前節點的人數+所有子問題返回的人數 num 之和，lu=所有子問題返回的路數 lu 之和，maxx=max( maxx,剛算出的總人數num/剛算出的路數lu+(1) ) } （括弧內的1分情況討論，若num整除lu則不加，不整除則加），所以3節點{num=15+6+5=26,lu=1+1=2,maxx=max(15,26/2=13)=15}。對於2節點{num=12+8=20,lu=0+1,maxx=(0,20/1)=20}，對於節點1{num=20+26+7=52,lu=1+2=3,maxx=max(20,15,52/3+1)=20}所以最後答案為20。

程式碼：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
vector<vector<int> >ro(200005);
ll num[200005];
struct node{
    ll lu,sum,maxx;
}now,get_solve;
node solve(int root){
    //cout<<"cont "<<root<<endl;
    if(ro[root].size()==0){
        now.lu=1;now.sum=num[root];now.maxx=num[root];
        return now;
    }
    ll lu=0,sum=num[root],maxx=0,mark=0;
    for(int i=0;i<ro[root].size();i++){
        get_solve=solve(ro[root][i]);
        lu+=get_solve.lu;
        sum+=get_solve.sum;
        maxx=max(get_solve.maxx,maxx);
    }
    now.lu=lu;now.sum=sum;
    if(sum%lu!=0) mark++;
    now.maxx=max(maxx,sum/lu+mark);
    return now;
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int n,get_num,mark=0;
    cin>>n;
    for(int i=2;i<=n;i++){
        cin>>get_num;
        ro[get_num].push_back(i);
    }
    for(int i=1;i<=n;i++){
        cin>>num[i];
    }
    node ans=solve(1);
    if(ans.sum%ans.lu!=0) mark++;
    cout<<max(ans.maxx,ans.sum/ans.lu+mark)<<endl;
    return 0;
}

View Code

 

Tags:

VirMach 便宜 VPS

QNews

QNews