3. Distributional Reinforcement Learning with Quantile Regression

2020 年 10 月 23 日
筆記
Deep Reinforcement Learning

C51演算法理論上用Wasserstein度量衡量兩個累積分布函數間的距離證明了價值分布的可行性，但在實際演算法中用KL散度對離散支援的概率進行擬合，不能作用於累積分布函數，不能保證Bellman更新收斂；且C51演算法使用價值分布的若干個固定離散支援，通過調整它們的概率來構建價值分布。

而分位數回歸(quantile regression)的distributional RL對此進行了改進。首先，使用了C51的「轉置」，即固定若干個離散支援的均勻概率，調整離散支援的位置；引入分位數回歸的思想，近似地實現了Wasserstein距離作為損失函數。

Quantile Distribution

假設\(\mathcal{Z}_Q\)是分位數分布空間，可以將它的累積概率函數均勻分為\(N\)等分，即\(\tau_0,\tau_1…,\tau_N(\tau_i=\frac{i}{N},i=0,1,..,N)\)。使用模型\(\theta:\mathcal{S}\times \mathcal{A}\to \mathbb{R}^N\)來預測分位數分布\(Z_\theta \in \mathcal{Z}_Q\)，即模型\(\{\theta_i (s,a)\}\)將狀態-動作對\((s,a)\)映射到均勻概率分布上。\(Z_\theta (s,a)\)的定義如下

\[Z_\theta (s,a):=\frac{1}{N}\sum_{i=1}^N \delta_{\theta_i(s,a)} \tag{1}
\]

其中，\(\delta_z\)表示在\(z\in\mathbb{R}\)處的Dirac函數

與C51演算法相比，這種做法的好處：

不再受預設定的支援限制，當回報的變化範圍很大時，預測更精確
取消了C51的投影步驟，避免了一些先驗知識
使用分位數回歸，可以近似最小化Wassertein損失，梯度下降不再有偏

Quantile Approximation

Quantile Projection

使用1-Wassertein距離對隨機價值分布\(Z\in \mathcal{Z}\)到\(\mathcal{Z}_Q\)的投影進行量化：

\[\mathcal{\Pi}_{W_1}Z:=\underset{{Z_\theta}\in\mathcal{Z}_Q}{\arg\min}W_1(Z,Z_\theta)
\]

假設\(Z_\theta\)的支援集為\(\{\theta_1,…,\theta_N \}\)，那麼

\[W_1(Z,Z_\theta)=\sum_{i=1}^N \int_{\tau_{i-1}}^{\tau_i} |F_Z^{-1}(w)-\theta_i|dw
\]

其中，\(\tau_i,\tau_{i-1}\in[0,1]\)論文指出，當\(F_Z^{-1}\)是逆累積分布函數時，\(F_Z^{-1}((\tau_{i-1}+\tau_i)/2)\)最小。因此，量化中點為\(\mathcal{\hat\tau_i}=\frac{\tau_{i-1}+\tau_i}{2}(1\le i\le N)\)，且最小化\(W_1\)的支援\(\theta_i=F_Z^{-1}(\mathcal{\hat\tau_i})\)。如下圖

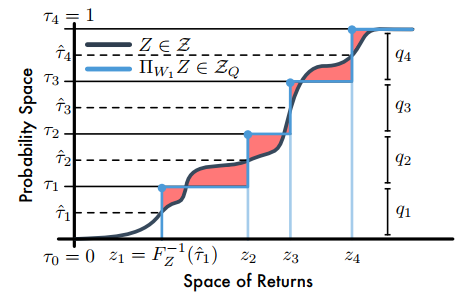
【注】C51是將回報空間(橫軸)均分為若干個支援，然後求Bellman運算元更新後回報落在每個支援上的概率，而分位數投影是將累積概率(縱軸)分為若干個支援(圖中是4個支援)，然後求出對應每個支援的回報值；圖中陰影部分的面積和就是1-Wasserstein誤差。

Quantile Regression

建立分位數投影后，需要去近似分布的分位數函數，需要引入分位數回歸損失。對於分布\(Z\)和一個給定的分位數\(\tau\)，分位數函數\(F_Z^{-1}(\tau)\)的值可以通過最小化分位數回歸損失得到

\[\mathcal{L}_{\text{QR}}^\tau(\theta):=\mathbb{E}_{\hat Z\sim Z}[\rho_\tau (\hat Z -\theta)],\quad \text{where} \quad \rho_\tau (u)=u(\tau-\delta_\{u<0\}),\forall u\in\mathbb{R}
\]

最終，整體的損失函數為

\[\sum_{i=1}^N \mathbb{E}_{\hat Z\sim Z}[\rho_{\hat{\tau}_i} (\hat Z -\theta)]
\]

但是，分位數回歸損失在0處不平滑。論文進一步提出了quantile Huber loss：

\[\mathcal{L}_{\mathcal{K}}(u)=
\begin{cases}
& \frac{1}{2}u^2,\quad\quad\quad\quad \text{if} |u|\le \mathcal{K} \\
& \mathcal{K}(|u|-\frac{1}{2}\mathcal{K}),\,\, \text{otherwise}
\end{cases}
\]

\[\rho_{\tau}^{\mathcal{K}}(u)=|\tau-\delta_{\{u<0\}}|\mathcal{L}_{\mathcal{K}}(u)
\]

Implement

QR TD-Learning

QRTD演算法(quantile regression temporal difference learning algorithm)的更新

\[\theta_i(s)\leftarrow \theta_i(s)+\alpha (\hat{\mathcal{\tau}}_i-\delta_{\{r+\gamma z^\prime < \theta_i (s) \}})
\]

\(a\sim\pi (\cdot|s),r\sim R(s,a),s^\prime\sim P(\cdot|s,a),z^\prime\sim Z_\theta(s^\prime)\)
其中，\(Z_\theta\)是由公式(1)給出的分位數分布，\(\theta_i (s)\)是狀態\(s\)下\(F_{Z^\pi (s)}^{-1}(\mathcal{\hat \tau}_i)\)的估計值。

QR-DQN

QR-DQN演算法偽程式碼

Append

1. Dirac Delta Function

\[\delta_a (x)=\delta (x-a)=0,(x\neq 0) \quad且\quad \int_{-\infty}^\infty \delta_a (x)d_x=1
\]

References

Will Dabney, Mark Rowland, Marc G. Bellemare, Rémi Munos. Distributional Reinforcement Learning with Quantile Regression. 2017.
Distributional RL

Tags: Deep Reinforcement Learning

3. Distributional Reinforcement Learning with Quantile Regression

Quantile Distribution