AVL樹概念

前面學習二叉查找樹和二叉樹的各種遍歷，但是其查找效率不穩定(斜樹)，而二叉平衡樹的用途更多。查找相比穩定很多。(歡迎關注數據結構專欄)

AVL樹是帶有平衡條件的二叉查找樹。這個平衡條件必須要容易保持。而且要保證它的深度是O(logN).
AVL的條件是左右樹的高度差（平衡因子）不大於1；並且它的每個子樹也都是平衡二叉樹。
對於平衡二叉樹的最小個數，n0=0;n1=1;nk=n(k-1)+n(k-2)+1;(求法可以類比斐波那契！)

難點：AVL是一顆二叉排序樹，用什麼樣的規則或者規律讓它能夠在複雜度不太高的情況下實現動態平衡呢？

不平衡概況

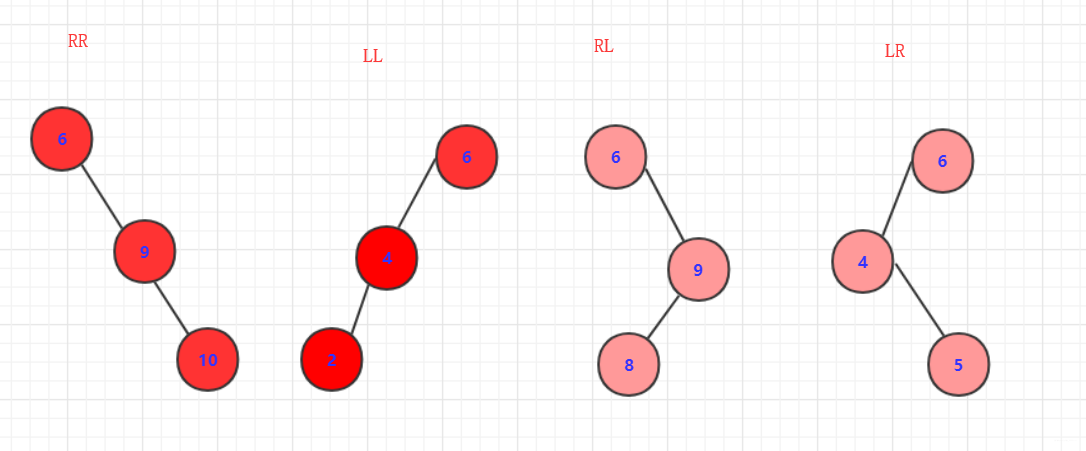
如果簡單的以單節點看，大致有上面四種情形，並且他們的最後結果也是有的有所相近。只是：上下會變動。該在左面的還在左面，改在右面的還在右面。

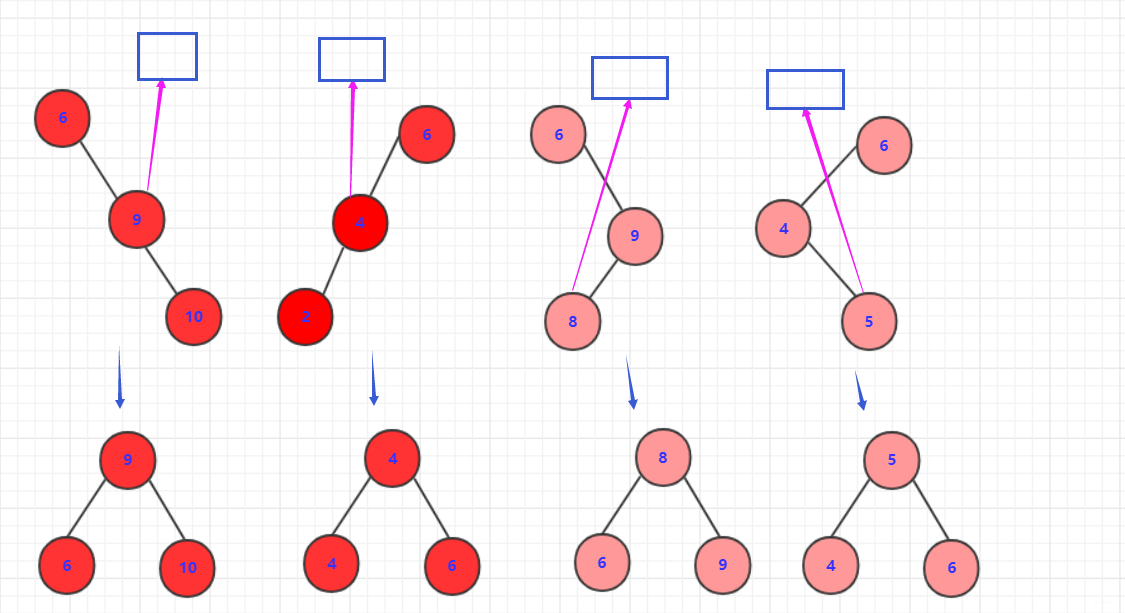
這只是針對在底部，對於可能出現的平衡要首先搞清楚：

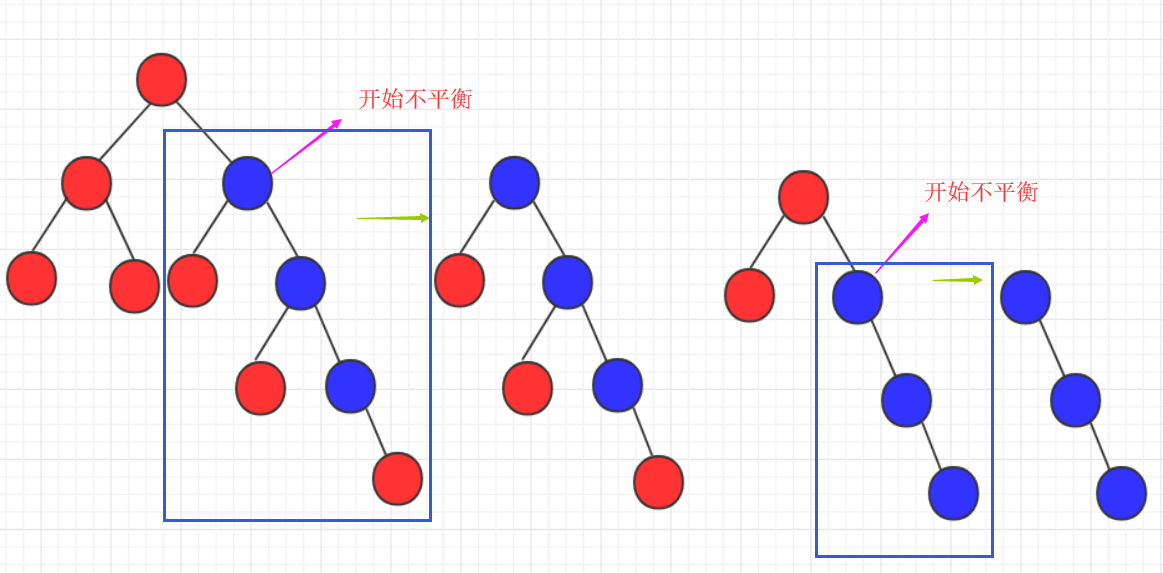
所以針對四種不平衡，可能出現在底部，也可能出現在頭，也可能出現在某個中間節點導致不平衡。 而我們只需要研究其首次不平衡點，解決之後整棵樹即繼續平衡。當然，在實際解決肯定會帶上遞歸的思想解決問題。

# 四種平衡旋轉方式

RR平衡旋轉(左單旋轉)

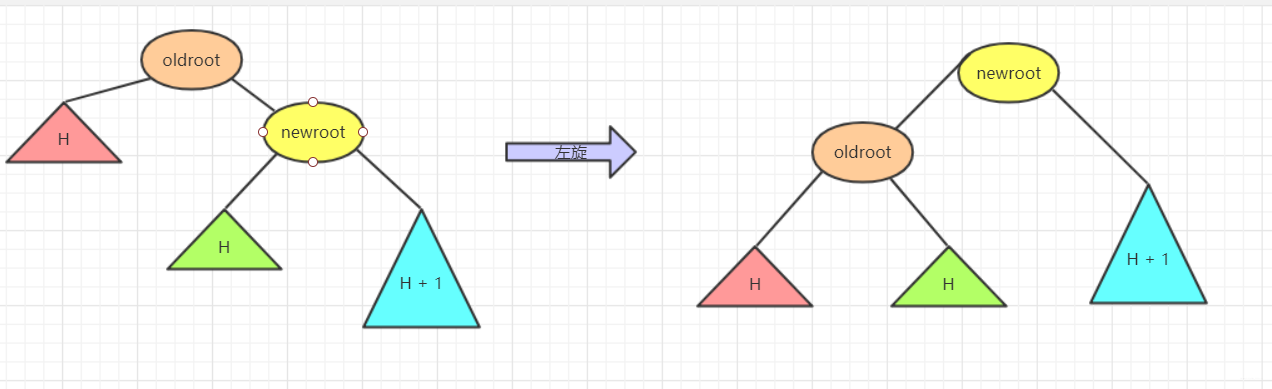
出現這種情況的原因是節點的右側的右側較深這時候不平衡節點需要左旋。再細看過程。

再左旋的過程中，root(oldroot)節點下沉，中間節點(newroot)上浮.而其中中間節點(newroot)的右側依然不變。
它上浮左側所以需要指向根節點(oldroot)(畢竟一棵樹)。但是這樣newroot原來左側節點H空缺。而我們需要仍然讓整個樹完整並且滿足二叉排序樹的規則。
而剛好本來oldroot右側指向newroot變成oldroot被newroot左側指向。所以oldroot右側空缺，剛好這個位置滿足在oldroot的右側。在newroot的左側。.所以我們將H插入在這個位置。
其中H可能為NULL。不過不影響操作！

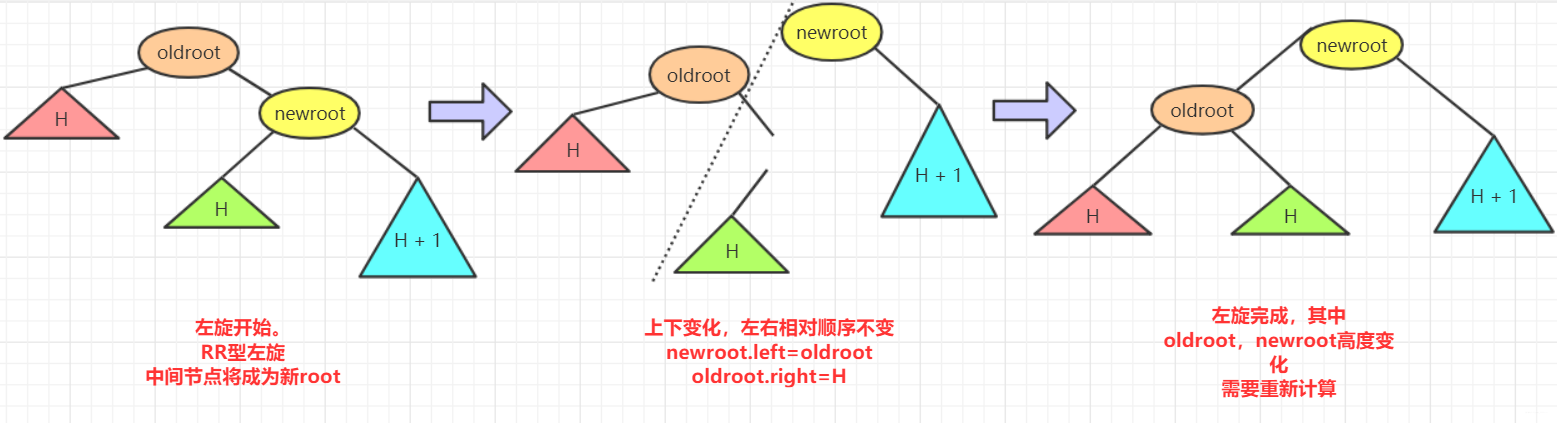
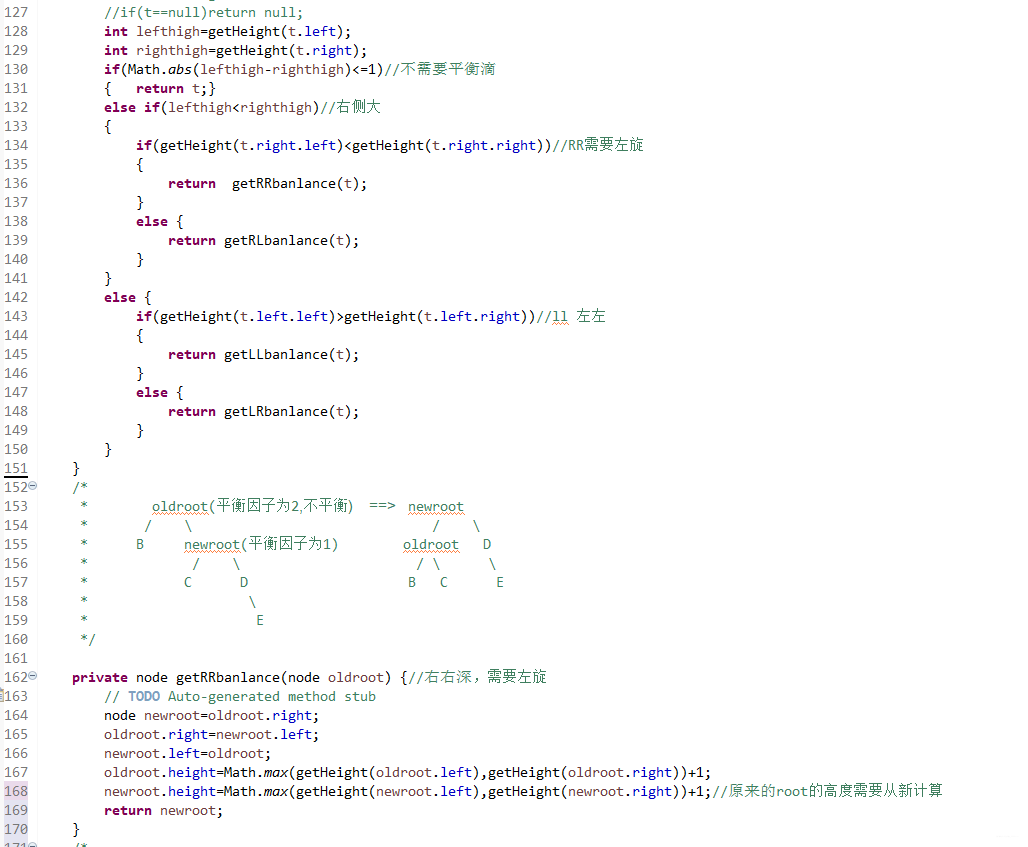
而左旋的程式碼可以表示為：

private node getRRbanlance(node oldroot) {//右右深，需要左旋      // TODO Auto-generated method stub      node newroot=oldroot.right;      oldroot.right=newroot.left;      newroot.left=oldroot;      oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;      newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新計算      return newroot;  }

LL平衡旋轉(右單旋轉)

而右旋和左旋相反，但是思路相同，根據上述進行替換即可！

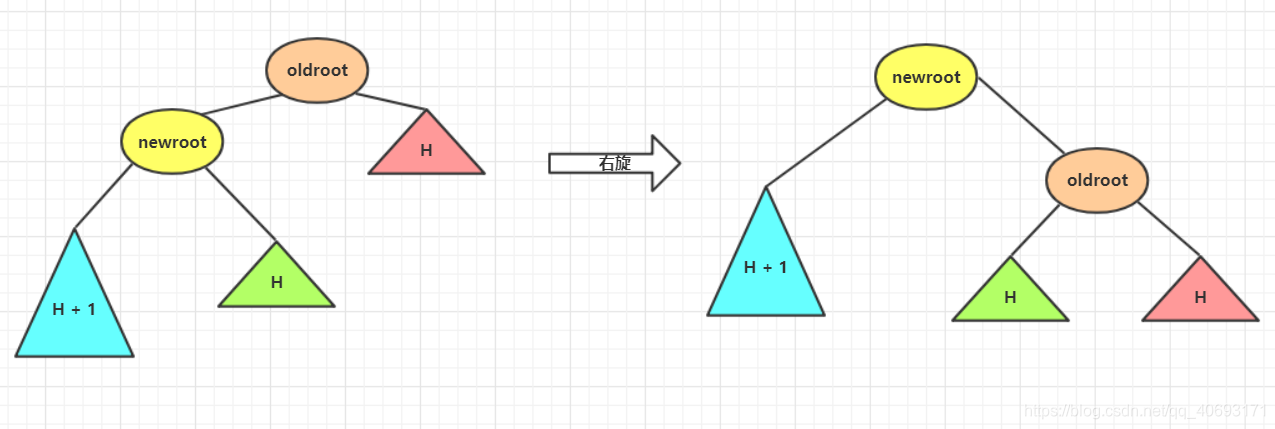
程式碼：

private node getLLbanlance(node oldroot) {//LL小，需要右旋轉      // TODO Auto-generated method stub      node newroot=oldroot.left;      oldroot.left=newroot.right;      newroot.right=oldroot;      oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;      newroot.height=Math.max(getHeight(newroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸      return newroot;  }

RL平衡旋轉(先右後左雙旋轉)

產生不平衡的條件原因是：

root節點右側左側節點的深度高些，使得與左側的差大於1.這個與我們前面看到的左旋右旋不同的是因為它的結構不能直接變一下就可以完成。
因為對於右左結構，中間的最大，兩側的最小。但是下面的比上面大(下面在上面右側)所以如果平衡的話，那麼右左的R.L應該在中間，而R應該在右側。原來的root在左側。
所以節點的變化浮動比較大，而且需要妥善處理各個子節點的移動使其滿足二叉排序樹的性質！
期間考慮樹高度變化即可！

這種雙旋轉其實也很簡單。不要被外表唬住。基於前面的單旋轉，雙旋轉有兩種具體邏輯思路。
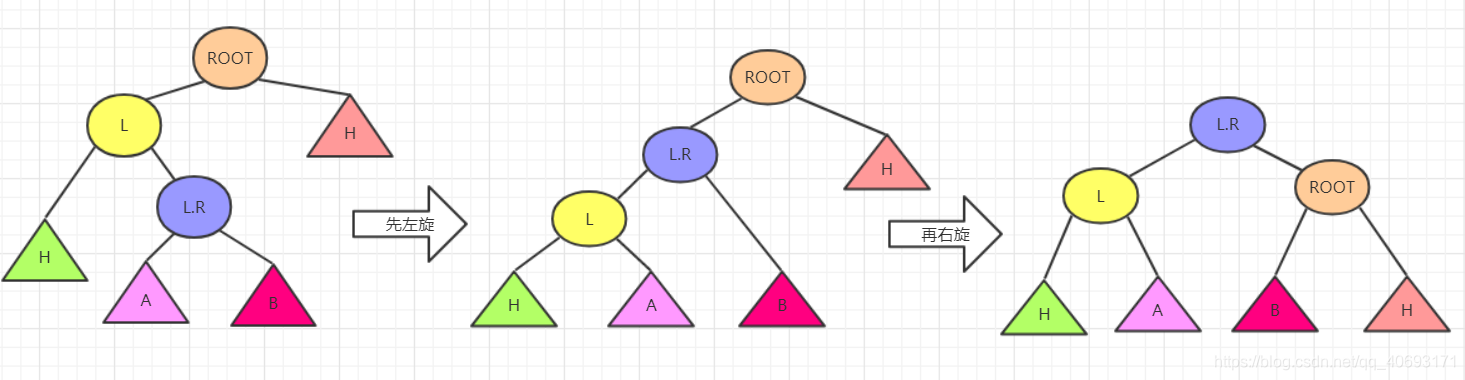
思路1：兩次旋轉RR,LL

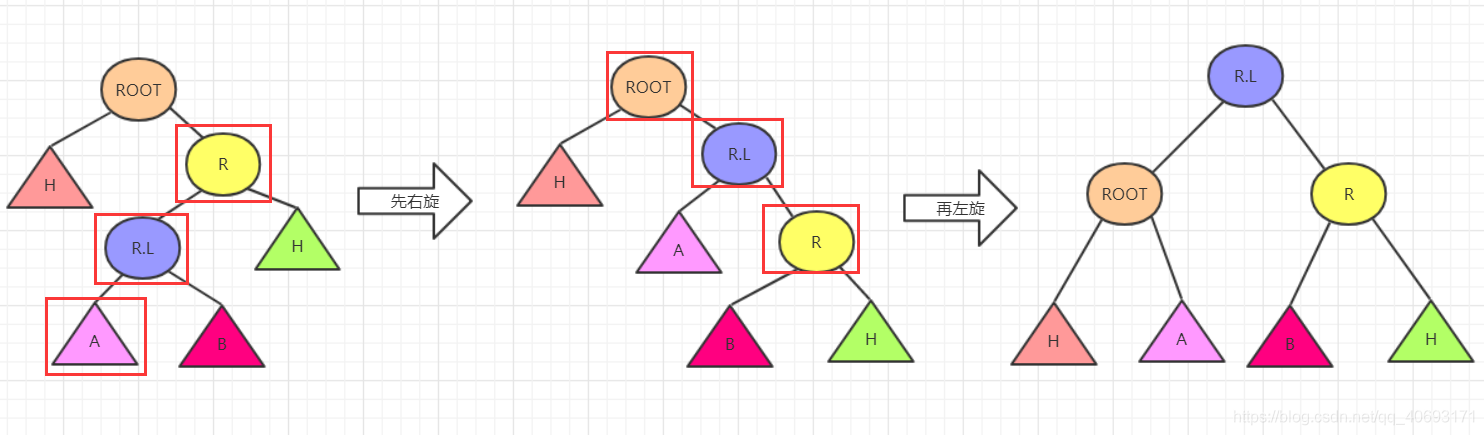
根據上圖所圈的，先對底部使得底部的大小關係變化，使其在滿足二叉平衡樹的條件下還滿足RR結構的二叉樹。所以只需要對右節點R先進行右旋,再對ROOT進行左旋即可。
思路2：直接分析
根據初始和結果的狀態，然後分析各個節點變化順序。手動操作這些節點即可！

首先根據ROOT,R,R.L三個節點變化。R.L肯定要在最頂層。左右分別指向ROOT和R。那麼這其中R.left，ROOT.right發生變化(原來分別是R,L和R)暫時為空。而剛好根據左右大小關係可以補上R.L的左右節點。
這樣思考整棵樹也可以完成平衡，但是要考慮樹的高度變化。

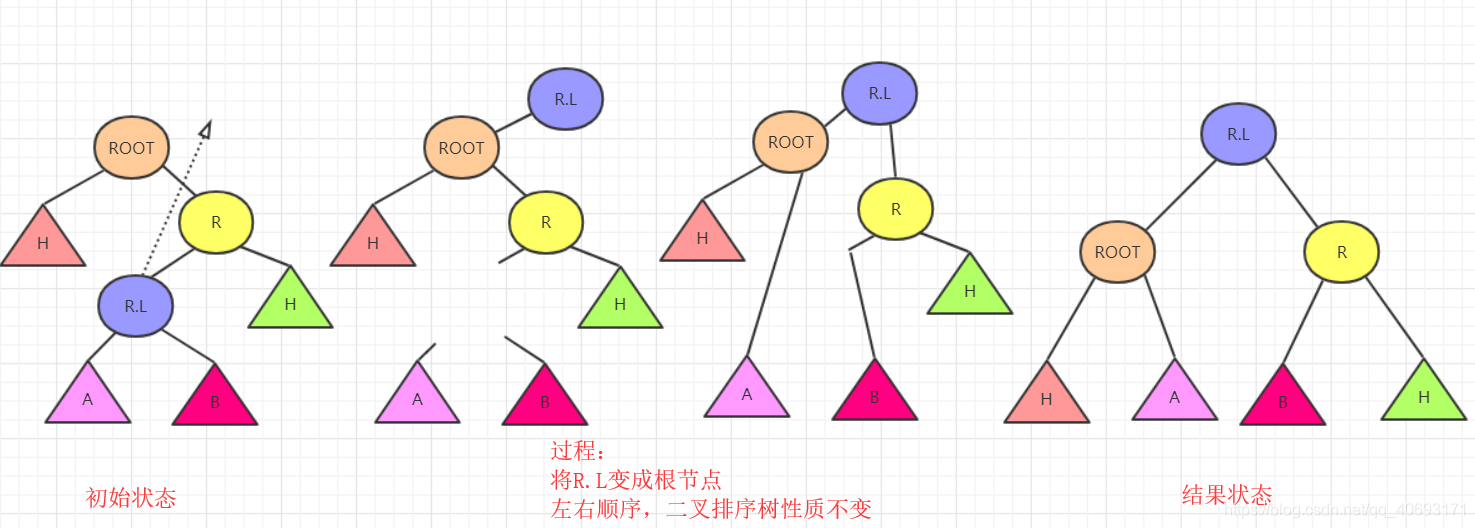
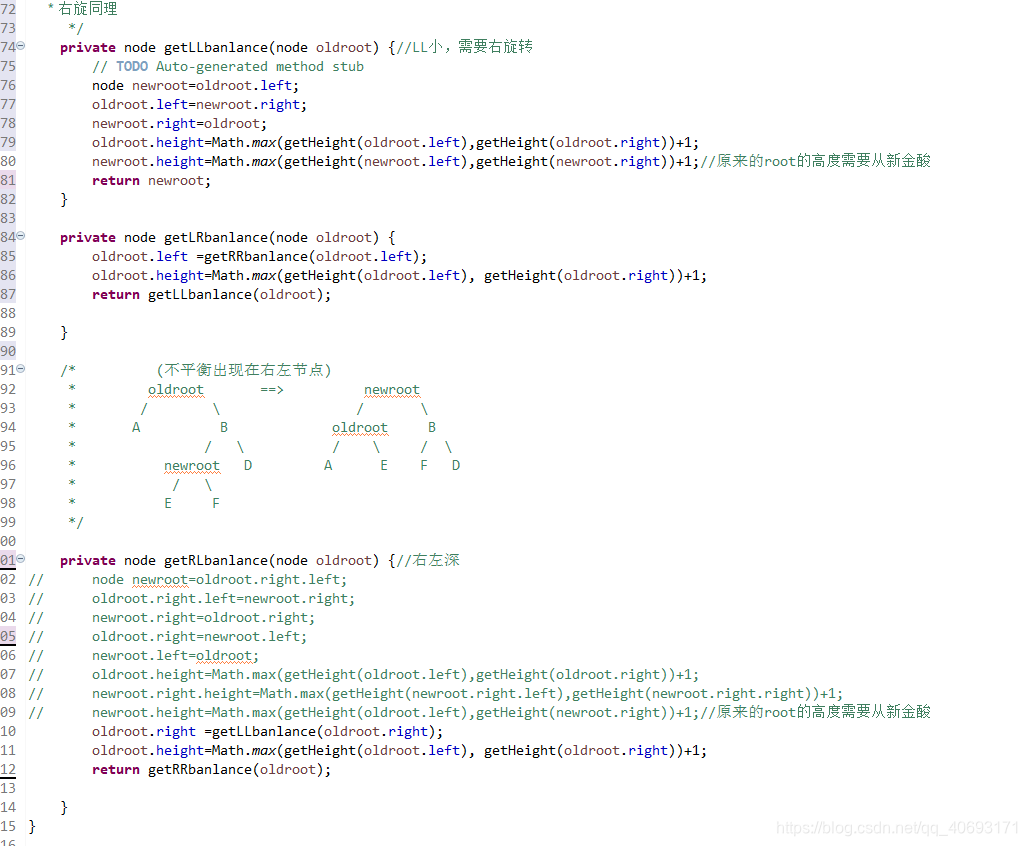
程式碼為：(注釋部分為方案1)

private node getRLbanlance(node oldroot) {//右左深  //      node newroot=oldroot.right.left;  //      oldroot.right.left=newroot.right;  //      newroot.right=oldroot.right;  //      oldroot.right=newroot.left;  //      newroot.left=oldroot;  //      oldroot.height=Math.max(getHeight(oldroot.left),getHeight(oldroot.right))+1;  //      newroot.right.height=Math.max(getHeight(newroot.right.left),getHeight(newroot.right.right))+1;  //      newroot.height=Math.max(getHeight(oldroot.left),getHeight(newroot.right))+1;//原來的root的高度需要從新金酸      oldroot.right =getLLbanlance(oldroot.right);      oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1;      return getRRbanlance(oldroot);        }

LR平衡旋轉(先左後右單旋轉)

根據上述RL修改即可

private node getLRbanlance(node oldroot) {      oldroot.left =getRRbanlance(oldroot.left);      oldroot.height=Math.max(getHeight(oldroot.left), getHeight(oldroot.right))+1;      return getLLbanlance(oldroot);        }

java程式碼實現

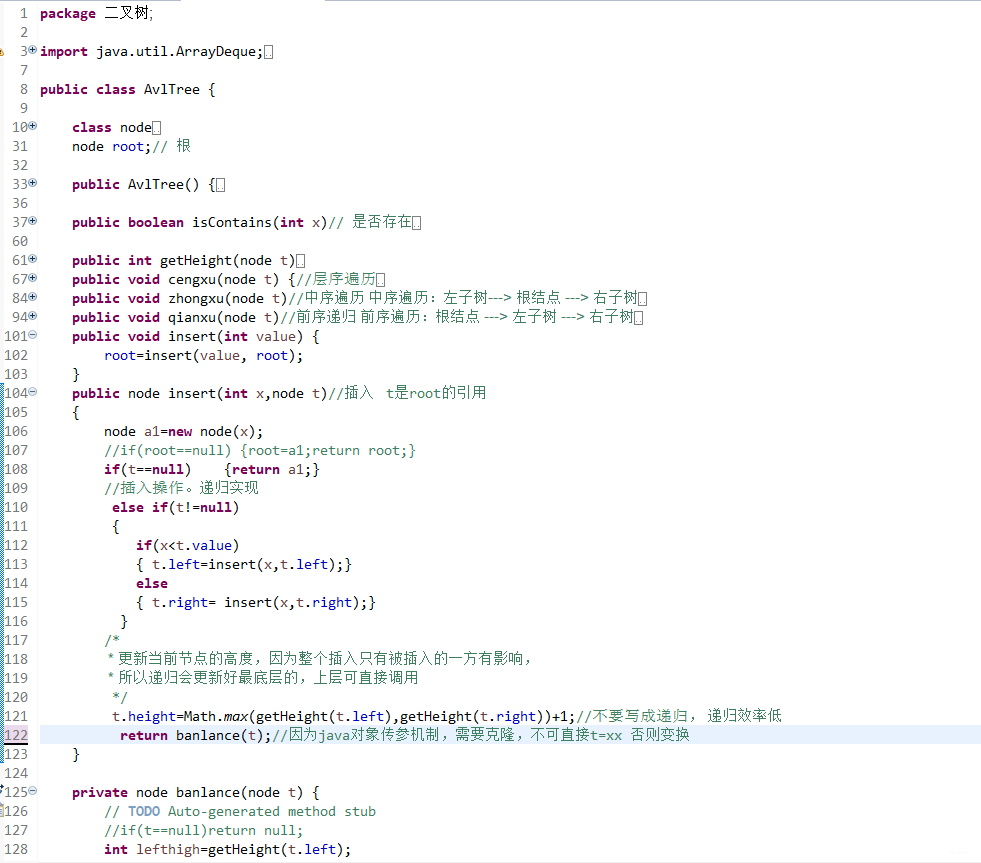
首先對於節點多個height屬性。用於計算高度(平衡因子)
插入是遞歸插入。遞歸一個來回的過程，去的過程進行插入。回的過程進行高度更新。和檢查是否平衡。不要寫全局遞歸計算高度，效率太低下。事實上高度變化只和插入和平衡有關，仔細考慮即不會有疏漏！

總結

測試情況：
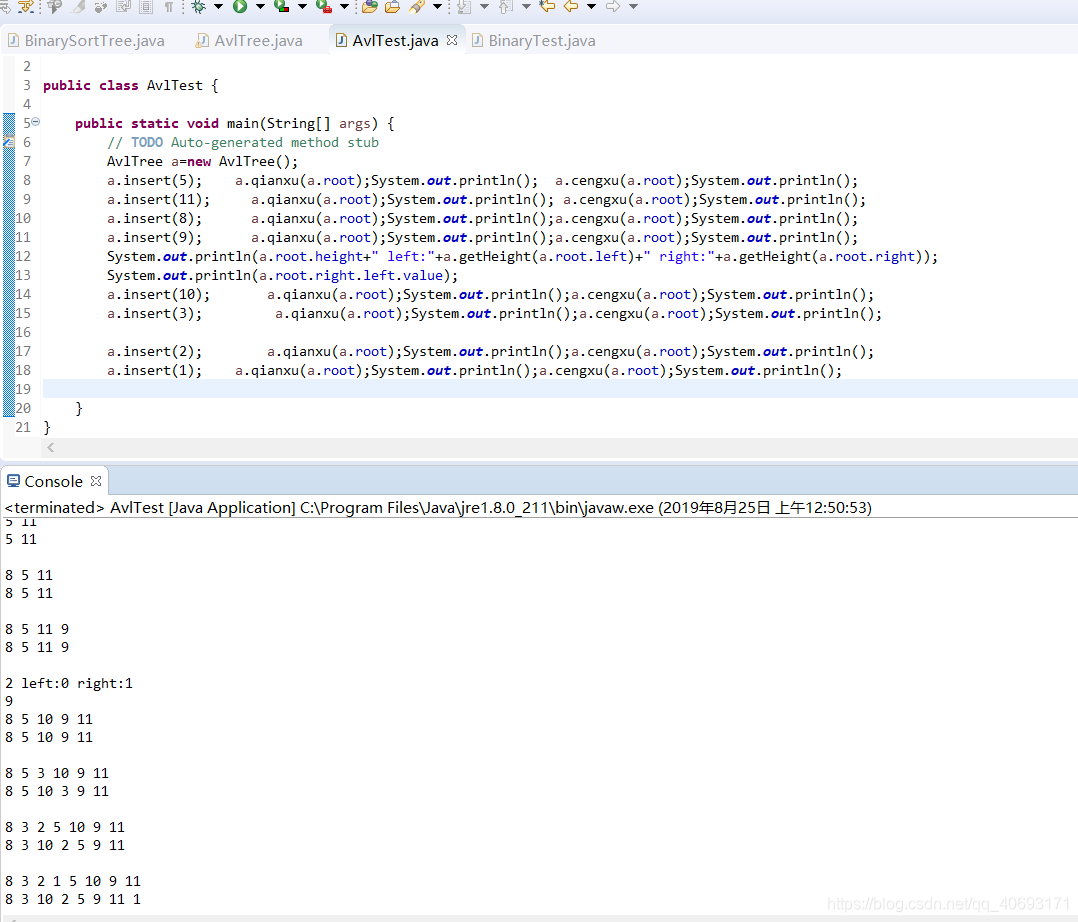
AVL的理解需要時間，當然筆者的AVL自己寫的可能有些疏漏，如果有問題還請各位一起探討！
當然，除了插入，AVL還有刪除等其他操作，(原理相似。刪除後平衡)有興趣可以一起研究。
如果需要源碼還請關注筆者公眾號：公眾號查看相關專題文章！
如果對後端、爬蟲、數據結構演算法等感性趣歡迎關注我的個人公眾號交流：bigsai(回復數據結構、爬蟲、java等有精心準備資料一份！)