【暢通工程 HDU – 1232 】【並查集模板題】
- 2019 年 10 月 3 日
- 筆記
並查集講解和模板
有一個博文對此分析的很透徹,附鏈接
為避免原鏈接失效,現摘錄如下:
為了解釋並查集的原理,我將舉一個更有愛的例子。
話說江湖上散落著各式各樣的大俠,有上千個之多。他們沒有什麼正當職業,整天背著劍在外面走來走去,碰到和自己不是一路人的,就免不了要打一架。但大俠們有一個優點就是講義氣,絕對不打自己的朋友。而且他們信奉「朋友的朋友就是我的朋友」,只要是能通過朋友關係串聯起來的,不管拐了多少個彎,都認為是自己人。這樣一來,江湖上就形成了一個一個的幫派,通過兩兩之間的朋友關係串聯起來。而不在同一個幫派的人,無論如何都無法通過朋友關係連起來,於是就可以放心往死了打。但是兩個原本互不相識的人,如何判斷是否屬於一個朋友圈呢?
我們可以在每個朋友圈內推舉出一個比較有名望的人,作為該圈子的代表人物。這樣,每個圈子就可以這樣命名「中國同胞隊」美國同胞隊」……兩人只要互相對一下自己的隊長是不是同一個人,就可以確定敵友關係了。
但是還有問題啊,大俠們只知道自己直接的朋友是誰,很多人壓根就不認識隊長要判斷自己的隊長是誰,只能漫無目的的通過朋友的朋友關係問下去:「你是不是隊長?你是不是隊長?」這樣,想打一架得先問個幾十年,餓都餓死了,受不了。這樣一來,隊長面子上也掛不住了,不僅效率太低,還有可能陷入無限循環中。於是隊長下令,重新組隊。隊內所有人實行分等級制度,形成樹狀結構,我隊長就是根節點,下面分別是二級隊員、三級隊員。每個人只要記住自己的上級是誰就行了。遇到判斷敵友的時候,只要一層層向上問,直到最高層,就可以在短時間內確定隊長是誰了。由於我們關心的只是兩個人之間是否是一個幫派的,至於他們是如何通過朋友關係相關聯的,以及每個圈子內部的結構是怎樣的,甚至隊長是誰,都不重要了。所以我們可以放任隊長隨意重新組隊,只要不搞錯敵友關係就好了。於是,門派產生了。
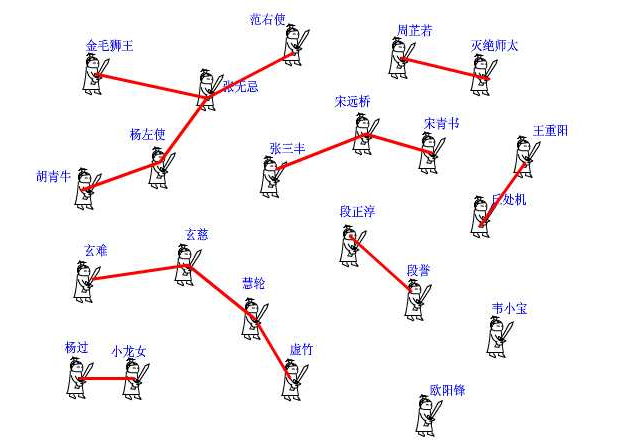
下面我們來看並查集的實現。 int pre[1000]; 這個數組,記錄了每個大俠的上級是誰。大俠們從1或者0開始編號(依據題意而定),pre[15]=3就表示15號大俠的上級是3號大俠。如果一個人的上級就是他自己,那說明他就是掌門人了,查找到此為止。也有孤家寡人自成一派的,比如歐陽鋒,那麼他的上級就是他自己。每個人都只認自己的上級。比如胡青牛同學只知道自己的上級是楊左使。張無忌是誰?不認識!要想知道自己的掌門是誰,只能一級級查上去。
find這個函數就是找掌門用的,意義再清楚不過了(路徑壓縮演算法先不論,後面再說)。
int unionsearch(int root) //查找根結點 { int son, tmp; son = root; while(root != pre[root]) //我的上級不是掌門 root = pre[root]; while(son != root) //我就找他的上級,直到掌門出現 { tmp = pre[son]; pre[son] = root; son = tmp; } return root; //掌門駕到~~ }再來看看join函數,就是在兩個點之間連一條線,這樣一來,原先它們所在的兩個板塊的所有點就都可以互通了。這在圖上很好辦,畫條線就行了。但我們現在是用並查集來描述武林中的狀況的,一共只有一個pre[]數組,該如何實現呢? 還是舉江湖的例子,假設現在武林中的形勢如圖所示。虛竹帥鍋與周芷若MM是我非常喜歡的兩個人物,他們的終極boss分別是玄慈方丈和滅絕師太,那明顯就是兩個陣營了。我不希望他們互相打架,就對他倆說:「你們兩位拉拉勾,做好朋友吧。」他們看在我的面子上,同意了。這一同意可非同小可,整個少林和峨眉派的人就不能打架了。這麼重大的變化,可如何實現呀,要改動多少地方?其實非常簡單,我對玄慈方丈說:「大師,麻煩你把你的上級改為滅絕師太吧。這樣一來,兩派原先的所有人員的終極boss都是師太,那還打個球啊!反正我們關心的只是連通性,門派內部的結構不要緊的。」玄慈一聽肯定火大了:「我靠,憑什麼是我變成她手下呀,怎麼不反過來?我抗議!」於是,兩人相約一戰,殺的是天昏地暗,風云為之變色啊,但是啊,這場戰爭終究會有勝負,勝者為王。弱者就被吞併了。反正誰加入誰效果是一樣的,門派就由兩個變成一個了。這段函數的意思明白了吧?
void join(int root1, int root2) //虛竹和周芷若做朋友 { int x, y; x = unionsearch(root1);//我老大是玄慈 y = unionsearch(root2);//我老大是滅絕 if(x != y) pre[x] = y; //打一仗,誰贏就當對方老大 }再來看看路徑壓縮演算法。建立門派的過程是用join函數兩個人兩個人地連接起來的,誰當誰的手下完全隨機。最後的樹狀結構會變成什麼樣,我也無法預知,一字長蛇陣也有可能。這樣查找的效率就會比較低下。最理想的情況就是所有人的直接上級都是掌門,一共就兩級結構,只要找一次就找到掌門了。哪怕不能完全做到,也最好盡量接近。這樣就產生了路徑壓縮演算法。
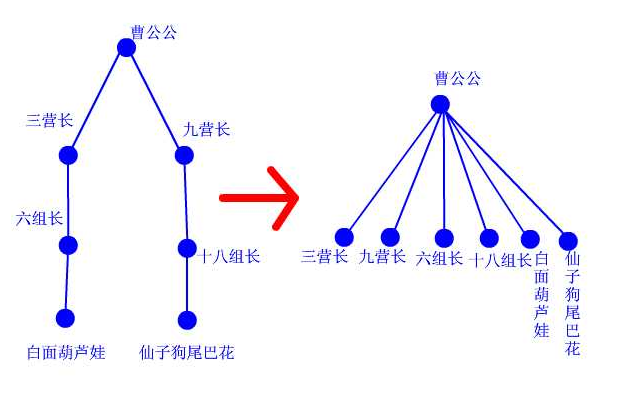
設想這樣一個場景:兩個互不相識的大俠碰面了,想知道能不能幹一場。 於是趕緊打電話問自己的上級:「你是不是掌門?」 上級說:「我不是呀,我的上級是誰誰誰,你問問他看看。」 一路問下去,原來兩人的最終boss都是東廠曹公公。 「哎呀呀,原來是自己人,有禮有禮,在下三營六組白面葫蘆娃!」 「幸會幸會,在下九營十八組仙子狗尾巴花!」 兩人高高興興地手拉手喝酒去了。 「等等等等,兩位大俠請留步,還有事情沒完成呢!」我叫住他倆。 「哦,對了,還要做路徑壓縮。」兩人醒悟。 白面葫蘆娃打電話給他的上級六組長:「組長啊,我查過了,其實偶們的掌門是曹公公。不如偶們一起結拜在曹公公手下吧,省得級別太低,以後查找掌門麻煩。」 「唔,有道理。」 白面葫蘆娃接著打電話給剛才拜訪過的三營長……仙子狗尾巴花也做了同樣的事情。 這樣,查詢中所有涉及到的人物都聚集在曹公公的直接領導下。每次查詢都做了優化處理,所以整個門派樹的層數都會維持在比較低的水平上。路徑壓縮的程式碼,看得懂很好,看不懂可以自己模擬一下,很簡單的一個遞歸而已。總之它所實現的功能就是這麼個意思。
於是,問題圓滿解決。。。。。。。。。
程式碼如下:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; int pre[1010]; //裡面全是掌門 int unionsearch(int root) { int son, tmp; son = root; while(root != pre[root]) //尋找掌門ing…… root = pre[root]; while(son != root) //路徑壓縮 { tmp = pre[son]; pre[son] = root; son = tmp; } return root; //掌門駕到~ } int main() { int num, road, total, i, start, end, root1, root2; while(scanf("%d%d", &num, &road) && num) { total = num - 1; //共num-1個門派 for(i = 1; i <= num; ++i) //每條路都是掌門 pre[i] = i; while(road--) { scanf("%d%d", &start, &end); //他倆要結拜 root1 = unionsearch(start); root2 = unionsearch(end); if(root1 != root2) //掌門不同?踢館!~ { pre[root1] = root2; total--; //門派少一個,敵人(要建的路)就少一個 } } printf("%dn", total);//天下局勢:還剩幾個門派 } return 0; }以上內容全部摘錄自那個部落格 , 現在接下來均為原創。
模板
並查集主要包括兩部分,查找root和合併兩個本不關聯的連通分支,查找root的目的正是為了將那些本不連通的部分相連。
int father[1010]; //存放第i個元素的父節點 int Find(int root) //查找根結點 { int son; son = root; while(root != father[root]) //尋找根結點 root = father[root]; while(son != root) //路徑壓縮 { int tmp = father[son]; father[son] = root; son = tmp; } return root; } void Union(int a, int b) //判斷是否連通,不連通就合併,判斷是否連通的手段是看他們的根(也就是上面講解中所說的掌門,而不單純的指它的上一級)是否是同一個 { int root1, root2; root1 = Find(a); root2 = Find(b); if(root1 != root2) //如果不連通,就把它們所在的連通分支合併 pre[root1] = root2; } //注意在main函數中將father數組中的每一個元素都賦值成它本身關於Find函數部分貌似用遞歸較快些,附程式碼如下:
int Find(int root) { if(root != father[root]) father[root] = Find(father[root]) ; //一步步去尋找最終的根節點 return father[root]; //root與father[root]相等會返回father[root],不相等同樣最終也會返回它 }題目講解及AC程式碼
講解
題目問最少還需要建設多少條道路才能使得全省任何兩個城鎮間都可以實現交通(但不一定有直接的道路相連,只要互相間接通過道路可達即可)。這剛好對應上面,將每個城鎮視為一個連通分支,其根節點也就是它自己,若是簡單的將它們連成一條線則需要建設N-1條路(N為城鎮數),倘若有兩個城鎮有一個共同的根節點則就會少建設一條路,這樣依據並查集即可解決這個問題。
AC程式碼
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int maxn = 1000 + 10; int father[maxn]; int N, M, num; int Find(int root) { if(root != father[root]) father[root] = Find(father[root]) ; //一步步去尋找最終的根節點 return father[root]; //root與father[root]相等會返回father[root],不相等同樣最終也會返回它 } int main() { // freopen("input.txt", "r", stdin); // freopen("output.txt", "w", stdout); while(scanf("%d", &N) && N) { scanf("%d", &M); for(int i = 1; i <= N; i++) father[i] = i; int num = N - 1; for(int i = 0; i < M; i++) { int a, b; scanf("%d%d", &a, &b); int f1 = Find(a), f2 = Find(b); if(f1 != f2) { father[f1] = f2; --num; } } cout << num << endl; } }