樹的基本概念
樹:
- 樹是一種遞歸數據結構,包含一個或多個數據節點的集合,其中一個節點被指定為樹的根節點,而其餘節點被稱為根的子節點。
- 除根節點以外的其他節點均被劃分為多個非空集,其中每個空集都稱為子樹。
- 樹的節點或者在它們之間保持父子關係,或者它們是姐妹節點。
- 在一般樹中,一個節點可以有任意數量的子節點,但只能有一個父節點。
- 下圖顯示了一棵樹,其中節點A是樹的根節點,而其他節點可以看作是A的孩子。
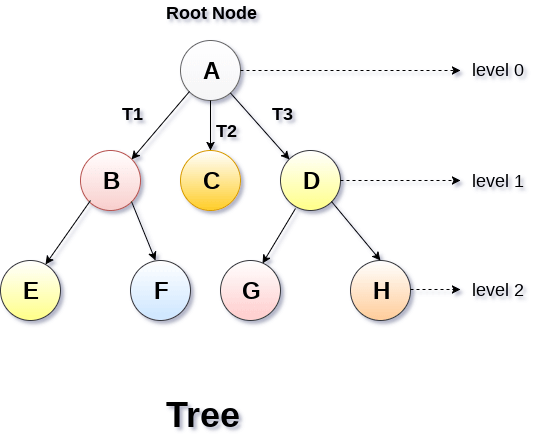
基本術語
- 根節點:-根節點是樹層次結構中的最高節點。換句話說,根節點是沒有任何父節點的節點。
- 子樹:-如果根節點不為空,則樹T1,T2和T3被稱為根節點的子樹。
- 葉子節點:-沒有任何子節點的樹的節點稱為葉子節點。葉節點是樹的最底部節點。普通樹中可以有任意數量的葉節點。葉節點也可以稱為外部節點。
- 程度:-節點的程度等於節點具有的子代數。在上圖所示的樹中,節點B的度為2。葉節點的度始終為0,而在完整的二叉樹中,每個節點的度均等於2。
二叉樹:
每個節點最多有2個節點的樹;
二叉樹的類型
1.嚴格二叉樹
每個非葉節點都包含非空的左右子樹
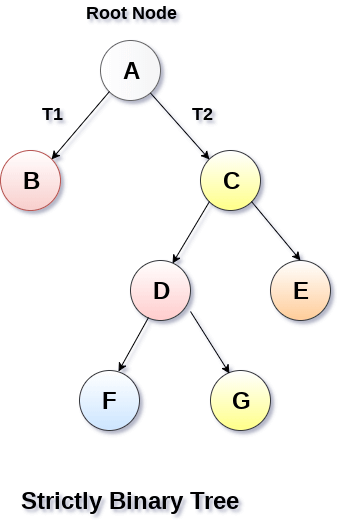
2.滿二叉樹(特殊的完全二叉樹)
所有的葉子節點都位於同一級。
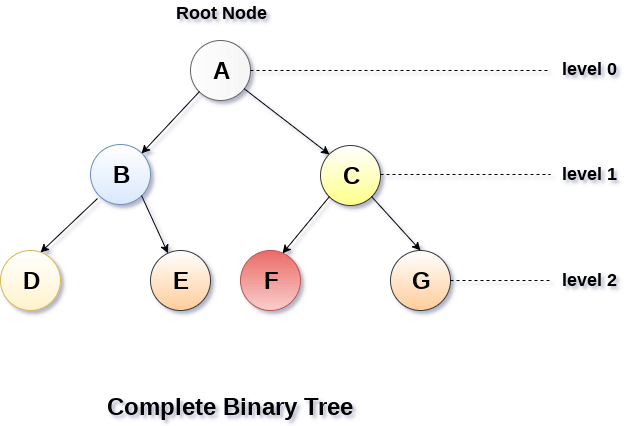
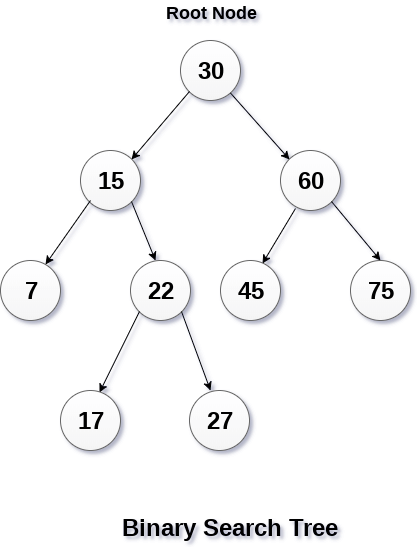
二叉排序樹:
二叉樹的基礎上滿足如下特性則為二叉排序樹;
- 若它的左子樹不為空,則左子樹的所有節點的值均小於它的根節點。
- 若它的右子樹不為空,則右子樹的所有節點的值均大於它的根節點。
- 它的左右子樹也分別為二叉排序樹。
優點:
- 在二叉搜索樹中搜索變得非常有效,因為我們在每一步都得到了提示,即哪個子樹包含所需的元素。
- 與數組和鏈表相比,二進位搜索樹被認為是有效的數據結構。在搜索過程中,它會在每個步驟中刪除一半的子樹。在二叉搜索樹中搜索元素需要o(log 2 n)時間。在最壞的情況下,搜索元素所需的時間為0(n)。
- 與數組和鏈表中的插入和刪除操作相比,它還加快了插入和刪除操作的速度。
二叉平衡樹(AVL):
所有節點的左右子樹的高度差小於1的二叉排序樹;

B樹:
所以,我們為了減少磁碟IO的次數,就你必須降低樹的深度,將「瘦高」的樹變得「矮胖」。
- 根節點必須至少含有2個節點。
- 除了根節點和葉節點之外,B樹中的每個節點至少包含m / 2個子節點。
- B樹中的每個節點最多包含m個子節點
- 所有葉節點必須處於同一級別。
B+樹:
B +樹是B樹的擴展,它允許有效的插入,刪除和搜索操作。
在B樹中,鍵和記錄都可以存儲在內部節點和葉節點中。而在B +樹中,記錄(數據)只能存儲在葉節點上,而內部節點只能存儲鍵值。
B +樹的葉節點以單鏈接列表的形式鏈接在一起,以使搜索查詢更高效。
B +樹用於存儲無法存儲在主存儲器中的大量數據。由於總是限制主存儲器的大小,因此B +樹的內部節點(訪問記錄的鍵)存儲在主存儲器中,而葉節點存儲在輔助存儲器中。
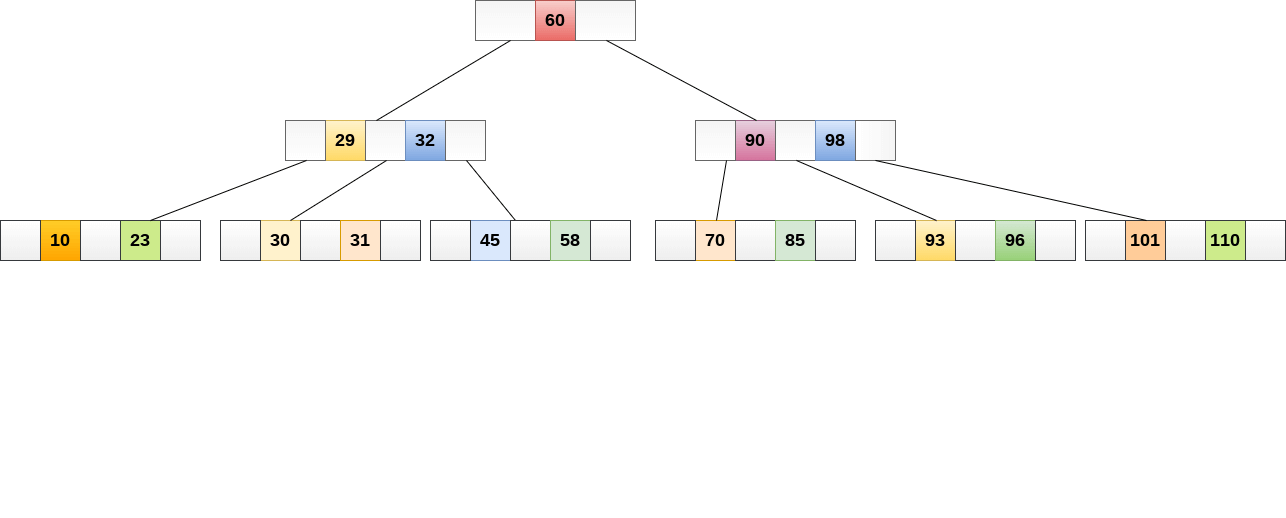
B +樹的內部節點通常稱為索引節點。下圖顯示了3級的B +樹。

B +樹的優勢
- 可以以相同數量的磁碟訪問來獲取記錄。
- 與B樹相比,樹的高度保持平衡並且較小。
- 我們可以依次或直接訪問存儲在B +樹中的數據。
- 鍵用於索引。
- 由於數據僅存儲在葉節點上,因此搜索查詢速度更快。
B樹VS B +樹
| SN | B樹 | B +樹 |
| 1個 | 搜索鍵不能重複存儲。 | 可能存在冗餘搜索鍵。 |
| 2 | 數據可以存儲在葉節點以及內部節點中 | 數據只能存儲在葉節點上。 |
| 3 | 搜索一些數據的過程較慢,因為可以在內部節點以及葉節點上找到數據。 | 由於只能在葉節點上找到數據,因此搜索相對較快。 |
| 4 | 內部節點的刪除是如此複雜且耗時。 | 刪除絕不會是一個複雜的過程,因為元素總是會從葉節點中刪除。 |
| 5 | 葉節點不能鏈接在一起。 | 葉節點鏈接在一起,使搜索操作更高效。 |
紅黑樹:
紅黑樹是一棵二叉搜索樹,它在每個節點上增加了一個存儲位來表示節點的顏色,可以是Red或Black。
通過對任意一條從根到葉子的簡單路徑上各個節點的顏色進行約束,紅黑樹確保沒有一條路徑會比其他路徑長出2倍,因而是近似平衡的。
特性:
- 每個節點要麼是紅色,要麼是黑色。
- 根節點是黑色。
- 葉子節點是黑色。
- 相鄰的兩個節點不能同時位紅色。
- 任意節點到其所有後代葉子節點的路徑上,都包含相同數目的黑色節點。
- 插入的節點一定是紅色。
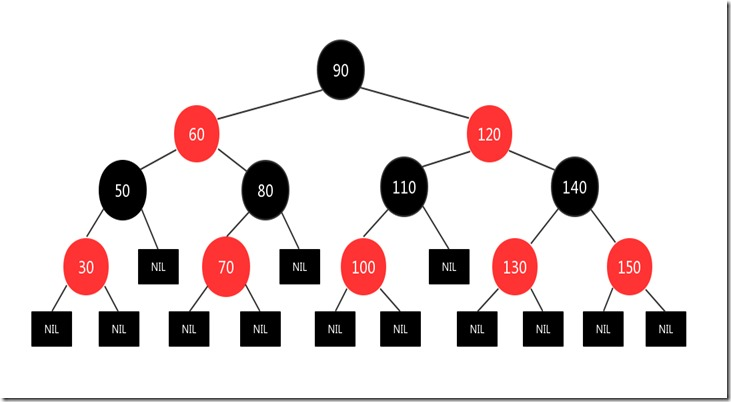
從某個節點x出發(不含該節點)到達一個葉節點的任意一條簡單路徑上的黑色節點個數成為該節點的黑高;
(以上如有錯誤或理解不到位地方歡迎指正)
參考資料:


