[點分治系列] 靜態點分
- 2019 年 11 月 5 日
- 筆記
沒錯…我就是要講點分治。這個東西原本學過的，當時學得不好…今天模擬賽又考這個東西結果寫不出來。
於是部落客專門又去學了學這個東西，這次絕對要搞懂了…【複賽倒計時：11天】
——正片開始——
點分是一個用來解決樹上路徑問題、距離問題的演算法。說直接點其實就是分治思想在樹上的體現和應用。
首先是分治的方法，既然是樹上問題，自然就是對樹進行分治。
我們對於一棵樹，選定一個點作為它的根，將這個點與其子樹拆開，然後對它的子樹也進行相同的操作，然後利用子樹統計答案。一般來說，點分更像一種思想，而不是一個演算法，當然你也可以把它當演算法來學。
關於怎麼選根來分樹，其他dalao的部落格已經講得非常清楚仔細了，每次選定一棵樹的重心，然後分它，這樣可以做到
O(nlogn)的優秀時間複雜度。
關於求重心，做法就是一個size統計。
這裡還是介紹一下吧（很多部落格都只貼一個程式碼…):
對於一個節點x，若我們把其刪除，原來的樹就會變成若干部分，我們設maxsubtree(x)表示刪除x後剩下的最大子樹的大小，若我們找到一個x，使得maxsubtree(x)最小，x就是這棵樹的重心。
給出求重心的程式碼：
void getroot(int x,int fa){ siz[x]=1;son[x]=0; for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(y==fa||vis[y])continue; getroot(y,x); siz[x]+=siz[y]; if(siz[y]>son[x])son[x]=siz[y]; } if(Siz-siz[x]>son[x])son[x]=Siz-siz[x]; if(son[x]<maxx)maxx=son[x],root=x; }
於是我們就知道怎麼拆樹了，後面的東西就不難了。
update: 19.11.5 對於上面的程式碼加一些解釋，siz表示當前在求重心的這一棵樹的大小，root用來記錄重心
我們來講如何統計資訊
首先我們要統計與每一次找到的重心有關的路徑，我們用dis[x]表示目標點（重心）到x的距離。
給出getdis的程式碼：
void getdis(int x,int fa,int d){//d表示x到目標點的距離 dis[++top]=d;//我們只需要知道每一個點到目標點的距離就行，不用知道這個點是哪個 for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(y==fa||vis[y])continue; getdis(y,x,d+val(i)); } }
有了dis數組後，我們就可以很輕鬆的獲得路徑的長度了。
比如，我們已知x到重心的距離是m，y到重心的距離是n，那x到y的距離就是m+n，可能細心的讀者已經發現鍋了。
如果x到y的路徑都在一棵子樹內，我們就會有一段距離被重複計算了，這樣我們得到的路徑就是不對的。
給一張圖理解一下：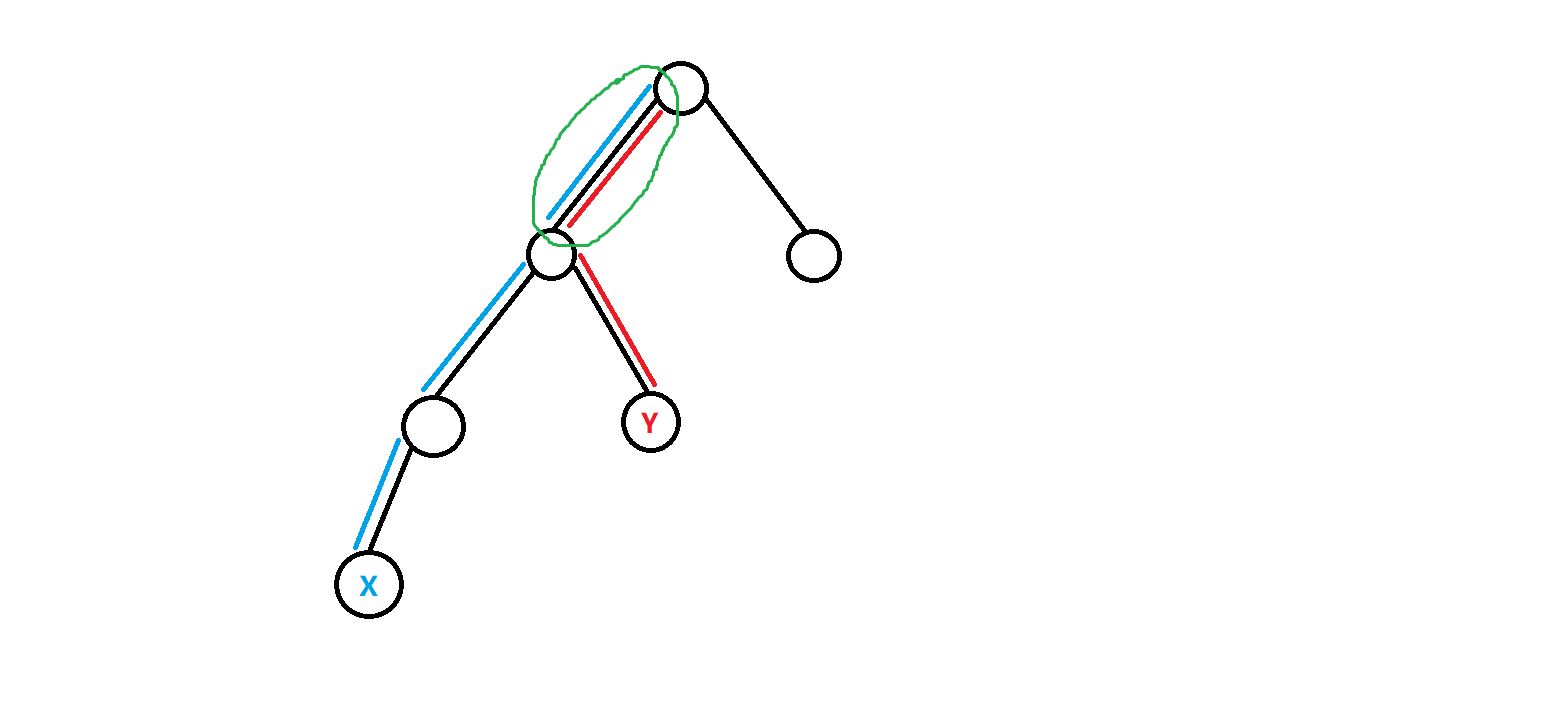
如圖，藍色的代表x到重心的路徑，紅色的代表y到重心的路徑，我們可以得到dis[x]=3，dis[y]=2。
如果按照前面說的計算方式，x到y的路徑長度應該是5了，但是並不是，我們的路徑長度是3。
原因就是，綠色的那一段，我們根本不走，我們不經過它。
於是我們要解決這種不合法路徑。知道所有路徑，又知道不合法路徑，利用容斥原理，我們可以得到：
合法路徑=所有路徑 – 不合法路徑。
這樣我們divide的程式碼就出來了：
void divide(int x){ vis[x]=1;//保證我們每次divide的x都是當前這棵樹的重心，所以標記x已經divide過了 solve(x,0,1);//計算這棵樹以x為重心的所有路徑答案 int totsiz=Siz;//這棵樹的大小 for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(vis[y])continue; solve(y,val(i),0);//求不合法路徑 maxx=inf,root=0;//初始化 Siz=siz[y]>siz[x]?totsiz-siz[x]:siz[y];//更新siz getroot(y,0);//求出以y為根的子樹 divide(root);//以y為根的子樹分治下去 } }
我們看一看去除不合法路徑的程式碼：
solve(y,val(i),-1);
思考發現：
所有不合法路徑都是在同一棵子樹中的路徑，我們要減去它。
先往下看完solve再回來看這裡。
我們進入到solve中，首先是getdis，以x為目標點獲取dis。但是我們要獲取的是距離為val(i)的dis。
這就使得dis[y]=val(i)，所以以y為根的子樹中的所有dis值就等於dis[y]+它們到y的距離，然後因為dis[y]是x到y的距離，
所以我們就求出了以y為根的子樹中所有點到x的距離。
實際一點的理解就是，y到目標點的距離是dis[y]=val(i)，y的子樹中的點到x的距離就是它們到y的距離+dis[y]，所以跑一遍可以求出y的子樹中所有點到x的距離。
然後就是solve函數了：
我們這裡的solve以模板題：【模板】點分治1 為例，不同題目我們solve的東西不同。
首先肯定可以想到一個O(n^2)的做法的，確實可以水過去這一題。
但是我畢竟是在寫部落格…所以，O(nlogn)做法奉上…
我們這麼想，我們需要統計路徑長為k的點對個數，那我們只要確定了一個點x，另一個點的dis[y]就應該是k-dis[x]，我們只需要二分找k-dis[x]就行了。
void solve(int x,int d,int avl){//avl(available)表示這次計算得到的答案是否合法 top=0;//清空dis數組 getdis(x,0,d);//獲取到當前這棵樹到x的距離為d的所有dis int cnt=0; sort(dis+1,dis+top+1);//排好序準備二分 dis[0]=-1;//第一個dis設置為奇怪的數方便下面比較 for(int i=1;i<=top;i++){//把所有距離相同的點放進一個桶裡面方便操作 if(dis[i]==dis[i-1]) bucket[cnt].amount++;//原來桶的個數+1 else bucket[++cnt].dis=dis[i],bucket[cnt].amount=1;//新開一個桶 } for(int i=1;i<=m;i++){ if(query[i]%2==0)//如果k是偶數的話，我們單獨考慮一下距離為k/2那些點，它們可以互相配對形成長為k的路徑 for(int j=1;j<=cnt;j++) if(bucket[j].dis==query[i]/2)//如果距離是k/2 ans[i]+=(bucket[j].amount-1)*bucket[j].amount/2*avl; //組合計數，假設我們有x個距離為k/2的點，就有(x-1)*x/2個點對距離為k，也就是我們可以配出這麼多個不同點對 //其實就是C(x,2)->x!/((x-2)!*2)->(x-1)*x/2 for(int j=1;j<=cnt&&bucket[j].dis<query[i]/2;j++){
//接著枚舉<k/2的距離，然後我們二分找>2的距離配對，避免重複(點對(u,v)和(v,u)是等價的)，等於k/2的我們前面算過了，所以所有情況都考慮到了 int l=j+1,r=cnt; while(l<=r){ int mid=(l++r)>>1; if(bucket[j].dis+bucket[mid].dis==query[i]){ ans[i]+=bucket[j].amount*bucket[mid].amount*avl; //組合計數記錄答案，假設我們有x個距離為m的點，y個距離為k-m的點，我們就有x*y個不同的點對(分類相乘) break;//這一輪二分完了，下一輪 } if(bucket[j].dis+bucket[mid].dis>query[i])r=mid-1;//大了，往小的二分 else l=mid+1;//小了，往大的二分 } } } }
這麼詳細都看不懂我就教不了了…
接下來就給出所有程式碼吧…（我知道你們只想看這個/doge）
#include<bits/stdc++.h> #define N 100010 #define lint long long #define inf 0x7fffffff using namespace std; int vis[N],son[N],Siz,maxx,siz[N]; int root,head[N],tot,n,m,dis[N],top,query[N],ans[N]; lint k; struct Bucket{ int dis,amount; }bucket[N]; struct Edge{ int nxt,to,val; #define nxt(x) e[x].nxt #define to(x) e[x].to #define val(x) e[x].val }e[N<<1]; inline int read(){ int data=0,w=1;char ch=0; while(ch!='-' && (ch<'0'||ch>'9'))ch=getchar(); if(ch=='-')w=-1,ch=getchar(); while(ch>='0' && ch<='9')data=data*10+ch-'0',ch=getchar(); return data*w; } inline void addedge(int f,int t,int val){ nxt(++tot)=head[f];to(tot)=t;val(tot)=val;head[f]=tot; } void getroot(int x,int fa){ siz[x]=1;son[x]=0; for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(y==fa||vis[y])continue; getroot(y,x); siz[x]+=siz[y]; if(siz[y]>son[x])son[x]=siz[y]; } if(Siz-siz[x]>son[x])son[x]=Siz-siz[x]; if(son[x]<maxx)maxx=son[x],root=x; } void getdis(int x,int fa,int d){ dis[++top]=d; for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(y==fa||vis[y])continue; getdis(y,x,d+val(i)); } } void solve(int rt,int d,int avl){//avl(available)表示這次計算得到的答案是否合法 top=0;//清空dis數組 getdis(rt,0,d);//獲取到當前這棵樹的rt的距離為d的所有dis int cnt=0; sort(dis+1,dis+top+1);//排好序準備二分 dis[0]=-1;//第一個dis設置為奇怪的數方便下面比較 for(int i=1;i<=top;i++){//把所有距離相同的點放進一個桶裡面方便操作 if(dis[i]==dis[i-1]) bucket[cnt].amount++;//原來桶的個數+1 else bucket[++cnt].dis=dis[i],bucket[cnt].amount=1;//新開一個桶 } for(int i=1;i<=m;i++){ if(query[i]%2==0)//如果k是偶數的話，我們單獨考慮一下距離為k/2那些點，它們可以互相配對形成長為k的路徑 for(int j=1;j<=cnt;j++) if(bucket[j].dis==query[i]/2)//如果距離是k/2 ans[i]+=(bucket[j].amount-1)*bucket[j].amount/2*avl; //組合計數，假設我們有x個距離為k/2的點，就有(x-1)*x/2個點對距離為k，也就是我們可以配出這麼多個不同點對 //其實就是C(x,2)->x!/((x-2)!*2)->(x-1)*x/2 for(int j=1;j<=cnt&&bucket[j].dis<query[i]/2;j++){//接著枚舉<k/2的距離，然後我們二分找>2的距離配對 int l=j+1,r=cnt; while(l<=r){ int mid=(l+r)>>1; if(bucket[j].dis+bucket[mid].dis==query[i]){ ans[i]+=bucket[j].amount*bucket[mid].amount*avl; //組合計數記錄答案，假設我們有x個距離為m的點，y個距離為k-m的點，我們就有x*y個不同的點對(分類相乘) break;//這一輪二分完了，下一輪 } if(bucket[j].dis+bucket[mid].dis>query[i])r=mid-1;//大了，往小的二分 else l=mid+1;//小了，往大的二分 } } } } void divide(int x){ vis[x]=1; solve(x,0,1);//合法的算進去 int totsiz=Siz; for(int i=head[x];i;i=nxt(i)){ int y=to(i); if(vis[y])continue; solve(y,val(i),-1);//不合法的算出來減掉 maxx=inf,root=0; Siz=siz[y]>siz[x]?totsiz-siz[x]:siz[y]; getroot(y,0); divide(root); } } int main(){ n=read();m=read(); for(int i=1;i<n;i++){ int x=read(),y=read(),z=read(); addedge(x,y,z);addedge(y,x,z); } for(int i=1;i<=m;i++)query[i]=read(); maxx=inf;root=0;Siz=n; getroot(1,0); divide(root); for(int i=1;i<=m;i++){ if(ans[i]>0)puts("AYE"); else puts("NAY"); } return 0; }
這份程式碼不僅求出了是否有路徑長為k的答案存在，還求出了路徑長為k的點對個數。
不需要求個數的話你就改一改solve，這樣常數會小一點，跑得更快，但是這一題我更想給你們講講思路，學會舉一反三…最後還是那句話，我個人並不認為點分是一種演算法，它更多體現的是分治的思想在樹上的應用。
其實你會發現，很多高端的數據結構、演算法之類的，都是由基礎的演算法思想衍生出來的泛用性更強的東西。
懂了基礎的演算法思想，你不但可以輕鬆的學會各種高階演算法，甚至可以自己造出解題的演算法。
比如圖論裡面的dijkstra最短路演算法，不就是貪心嗎？再比如線段樹，不就是分治嗎？
一些看起來很高級，聽起來很難的東西，只要你弄明白了其中的本質，你在感嘆發明者的智慧同時，自己也就收穫到了其中蘊含的知識和基礎思想的應用方法。學習不是死學…只有弄明白了它的工作原理和方式，你才算是掌握了它，僅僅是可以用它來做題，那題目變變形，你就一臉懵了。
