【計算幾何 01】叉積
- 2020 年 9 月 23 日
- 筆記
- 演算法基礎:計算幾何
這幾天閑來無事去學習了一下計算幾何,發現其實不(sang)是(xin)太(bing)難(kuang)😛
今天就重點介紹一下簡單的叉積及其簡單的運用(畢竟作為蒟蒻,難的搞不來啊)
什麼是計算幾何?
「對幾何外形資訊的電腦表示、分析和綜合」——福雷斯特
其實所謂計算幾何,就是用電腦去解決不同維度上的幾何問題,而我們要做的,就是設計一套演算法,讓電腦去分析和解決一系列的幾何問題。
一些基本知識
坐標的存儲
一般來說,計算幾何都涉及到了小數坐標,這時開一個含兩個double類型的結構體就比較穩健,我一般的定義如下:
struct node//定義一個點
{
double x,y;
}a[11000];
線段的存儲
聰明絕頂的你肯定已經想到了,線段就是包含兩個點的一個結構體,所以我一般的定義如下
struct line//定義一條線
{
node p1,p2;
} list[11000];
叉積
終於到今天的主角—叉積了!😝
那麼什麼是叉積呢?叉積其實是兩個矢量模的乘積再乘夾角正弦,經過推導可以發現兩個向量\(A(x1,y1),B(x2,y2)\)的叉積為:
\]
先丟出程式碼:
double multi(node p1,node p2,node p0)//計算叉積,p1,p2,p0都為點
{
double x1,y1,x2,y2;
x1=p1.x-p0.x;
y1=p1.y-p0.y;
x2=p2.x-p0.x;
y2=p2.y-p0.y;
return x1*y2-x2*y1;
}
這就是傳說中的叉積計算了!是不是很短呢,那就讓我們來理解一下這個multi函數吧。
由於叉積是向量間的運算,大家都知道向量可以用末坐標減去首坐標得到,那麼其實multi函數計算的就是向量A(x1,y1)與向量B(x2,y2)的叉積。
對於multi函數的意義,首先multi的正負是有特殊含義的:以p0為參考點,如果multi大於0,則p2在p1的逆時針方向,反正,如果multi小於0,則p2在p1的順時針方向,特殊的,當multi等於0,p1、p2、p0三點共線。

其次,multi的值也是有含義的!通過後面的學習你就會發現,multi的絕對值就是以p0、p1、p2三點構成的三角形的面積的兩倍!利用這個規律,可以完成很多與計算幾何有關的題目。
一些簡單的運用
【caioj 1212 判斷線段相交(跨立實驗)】
題目描述
【題意】
有n條線段(編號為1~n),按1~n的順序放在二維坐標繫上(就是先放1號,再放2號……),
要求輸出最上面的那些線段的編號(就是沒有其他線段壓在它上面的那些線段)
【輸入格式】
第一行第一個數n( 1 <= n <= 10000)表示這組數據有n條線段。
下來n行,每行兩個坐標,表示第i條線段的兩個端點。
【輸出格式】
一行。輸出最上面的線段的編號(從小到大)。相鄰兩個編號用空格隔開,最後一個編號沒有空格。
【樣例1輸入】
5
1 1 4 2
2 3 3 1
1 -2.0 8 4
1 4 8 2
3 3 6 -2.0
【樣例1輸出】
2 4 5
【樣例2輸入】
3
0 0 1 1
1 0 2 1
2 0 3 1
【樣例2輸出】
1 2 3
這道題很明顯要讓我們判斷任意兩條線段是否相交,這就要用到剛剛講到的叉積的第一種用法了!
很明顯,相交有兩種情況,相交且穿過和相交但不穿過(如下圖)
我們首先先討論第一種情況,如何判斷兩條直線相交且穿過?

如上圖,先假設兩條直線為L1和L2,每條直線的兩個端點分別為p1和p2,那麼如果以
L1.p1為一個參考點,如果L1.p2在L2.p1與L2.p2中間;再以L2.p1為參考點,如果L2.p2在L1.p1與L1.p2中間,那麼就可以判斷L1與L2相交且穿過(如下圖)

這種情況非常好理解吧,下一種情況就更加簡單了,僅需討論哪三個點在一條「直線」上(畢竟不穿過,所以必有三點共線),然後判斷一下
不穿過的那個點是否在一條「線段」上(如下圖)

具體程式碼如下
double check(line l1,line l2)//判斷是否相交
{
if(multi(l2.p1,l1.p2,l1.p1)*multi(l1.p2,l2.p2,l1.p1)>0)//判斷以L1.p1為基準,L1.p2是否在L2.p1與L2.p2中間
if(multi(l1.p1,l2.p2,l2.p1)*multi(l2.p2,l1.p2,l2.p1)>0)//判斷以L2.p1為基準,L2.p2是否在L1.p1與L2.p2中間
return true;//大部分情況下,能判斷兩直線相交
if(multi(l1.p1,l1.p2,l2.p1)==0)if(mymin(l1.p1.x,l1.p2.x)<=l2.p1.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p1.x)if(mymin(l1.p1.y,l1.p2.y)<=l2.p1.y)if(mymax(l1.p1.y,l1.p2.y)>=l2.p1.y)return true;
if(multi(l1.p1,l1.p2,l2.p2)==0)if(mymin(l1.p1.x,l1.p2.x)<=l2.p2.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p2.x)if(mymin(l1.p1.y,l1.p2.y)<=l2.p2.y)if(mymax(l1.p1.y,l1.p2.y)>=l2.p2.y)return true;
if(multi(l2.p1,l2.p2,l1.p1)==0)if(mymin(l2.p1.x,l2.p2.x)<=l1.p1.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p1.x)if(mymin(l2.p1.y,l2.p2.y)<=l1.p1.y)if(mymax(l2.p1.y,l2.p2.y)>=l1.p1.y)return true;
if(multi(l2.p1,l2.p2,l1.p2)==0)if(mymin(l2.p1.x,l2.p2.x)<=l1.p2.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p2.x)if(mymin(l2.p1.y,l2.p2.y)<=l1.p2.y)if(mymax(l2.p1.y,l2.p2.y)>=l1.p2.y)return true;
//判斷兩條直線相交且一條直線端點在另一條直線上
return false;
}
在之前的版本里,我在判斷兩條直線相交且一條直線端點在另一條直線上的情況中忽略了兩條直線互相一條與x軸垂直,一條與y軸垂直,且某一條延伸出去恰好交於另一條直線交點的情況,於是在一次比賽中WA了十多發QwQ,下面放上錯誤程式碼以作為警示:
double check(line l1,line l2)//判斷是否相交
{
if(multi(l2.p1,l1.p2,l1.p1)*multi(l1.p2,l2.p2,l1.p1)>0)//判斷以L1.p1為基準,L1.p2是否在L2.p1與L2.p2中間
if(multi(l1.p1,l2.p2,l2.p1)*multi(l2.p2,l1.p2,l2.p1)>0)//判斷以L2.p1為基準,L2.p2是否在L1.p1與L2.p2中間
return true;//大部分情況下,能判斷兩直線相交 if(multi(l2.p1,l1.p1,l1.p2)==0)if(mymin(l1.p1.x,l1.p2.x<=l2.p1.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p1.x)return true;
if(multi(l2.p2,l1.p1,l1.p2)==0)if(mymin(l1.p1.x,l1.p2.x<=l2.p2.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p2.x)return true;
if(multi(l1.p1,l2.p1,l2.p2)==0)if(mymin(l2.p1.x,l2.p2.x<=l1.p1.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p1.x)return true;
if(multi(l1.p2,l2.p1,l2.p2)==0)if(mymin(l2.p1.x,l2.p2.x<=l1.p2.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p2.x)return true;
//判斷兩條直線相交且一條直線端點在另一條直線上
return false;
}
主程式就很簡單了,一條一條邊讀入,讀入第i條邊時判斷他與前i-1條邊是否相交,若相交,這之前的邊j被蓋住,判斷數組bo【j】=1。最後統計bo【i】==0的邊就好啦
附上完整程式碼:
#include<cmath>
#include<cstdlib>
#include<cstdio>
#include<cstring>
using namespace std;
struct node//定義一個點
{
double x,y;
};
struct line//定義一條線
{
node p1,p2;
} list[11000];
int a[11000]={0};
bool bo[11000]={0};
int i,j,k,m,n,o,p,js,jl,jk,len;
//================================
double mymax(double x,double y)//求max
{
if(x>y)return x;
else return y;
}
double mymin(double x,double y)//求min
{
if(x<y)return x;
else return y;
}
//=================================
double multi(node p1,node p2,node p0)//計算叉積:而且值為三點構成三角形的面積的兩倍
{
double x1,y1,x2,y2;
x1=p1.x-p0.x;
y1=p1.y-p0.y;
x2=p2.x-p0.x;
y2=p2.y-p0.y;
return x1*y2-x2*y1;
}
double check(line l1,line l2)//判斷是否相交
{
if(multi(l2.p1,l1.p2,l1.p1)*multi(l1.p2,l2.p2,l1.p1)>0)//判斷以L1.p1為基準,L1.p2是否在L2.p1與L2.p2中間
if(multi(l1.p1,l2.p2,l2.p1)*multi(l2.p2,l1.p2,l2.p1)>0)//判斷以L2.p1為基準,L2.p2是否在L1.p1與L2.p2中間
return true;//大部分情況下,能判斷兩直線相交
if(multi(l1.p1,l1.p2,l2.p1)==0)if(mymin(l1.p1.x,l1.p2.x)<=l2.p1.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p1.x)if(mymin(l1.p1.y,l1.p2.y)<=l2.p1.y)if(mymax(l1.p1.y,l1.p2.y)>=l2.p1.y)return true;
if(multi(l1.p1,l1.p2,l2.p2)==0)if(mymin(l1.p1.x,l1.p2.x)<=l2.p2.x)if(mymax(l1.p1.x,l1.p2.x)>=l2.p2.x)if(mymin(l1.p1.y,l1.p2.y)<=l2.p2.y)if(mymax(l1.p1.y,l1.p2.y)>=l2.p2.y)return true;
if(multi(l2.p1,l2.p2,l1.p1)==0)if(mymin(l2.p1.x,l2.p2.x)<=l1.p1.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p1.x)if(mymin(l2.p1.y,l2.p2.y)<=l1.p1.y)if(mymax(l2.p1.y,l2.p2.y)>=l1.p1.y)return true;
if(multi(l2.p1,l2.p2,l1.p2)==0)if(mymin(l2.p1.x,l2.p2.x)<=l1.p2.x)if(mymax(l2.p1.x,l2.p2.x)>=l1.p2.x)if(mymin(l2.p1.y,l2.p2.y)<=l1.p2.y)if(mymax(l2.p1.y,l2.p2.y)>=l1.p2.y)return true;
//判斷兩條直線相交且一條直線端點在另一條直線上
return false;
}
//==================================
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf%lf%lf",&list[i].p1.x,&list[i].p1.y,&list[i].p2.x,&list[i].p2.y);
for(int i=1;i<n;i++)
for(int j=i+1;j<=n;j++)
{
if(check(list[i],list[j]))//判斷相交
{
bo[i]=1;
break;
}
}
len=0;
for(int i=1;i<=n;i++)if(bo[i]==0)a[++len]=i;
for(int i=1;i<len;i++)printf("%d ",a[i]);
printf("%d\n",a[len]);
return 0;
}
【caioj 1213 面積】
題目描述
【題意】
在一個平面坐標繫上隨意畫一條有n個點的封閉折線(按畫線的順序給出點的坐標),保證封閉折線的任意兩條邊都不相交。最後要計算這條路線包圍的面積。
【輸入格式】
第一行整數 n (3 <= n <= 1000),表示有n個點。
下來n行,每行兩個整數x(橫坐標)和y(縱坐標),表示點坐標(-10000<x,y<=10000)。
【輸出格式】
一行一個實數,即封閉折線所包圍的面積(保留4位小數)。
【樣例1輸入】
4
2 1
5 1
5 5
2 5
【樣例1輸出】
12.0000
【樣例2輸入】
5
2 1
5 1
3 2
5 3
2 3
【樣例2輸出】
4.0000
這道題對比上一道題就簡單很多了,這道題要用到叉積的第二種用法——計算面積!對於任意一個多邊形,只要以一號點p1為參考點,枚舉任意兩個相鄰的點pi和pi-1(i>=3),帶符號計算p1和pi、pi-1所構成的三角形的面積(multi(pi,pi-1,p1)/2),累加取絕對值就是答案了。
至於為什麼要帶符號運算,請看我用下面這幅圖演示

對於這個多邊形,首先先加上multi(p3,p2,p1)/2的值(由於p3在p2的逆時針方向,所以為正)即為加上了紅色部分
然後再加上multi(p4,p3,p1)/2的值(由於p4在p3的順時針方向,所以為負)即為減去了綠色部分

然後再加上multi(p5,p4,p1)/2的值(由於p5在p4的逆時針方向,所以為正)即為加上了黃色部分,就是答案了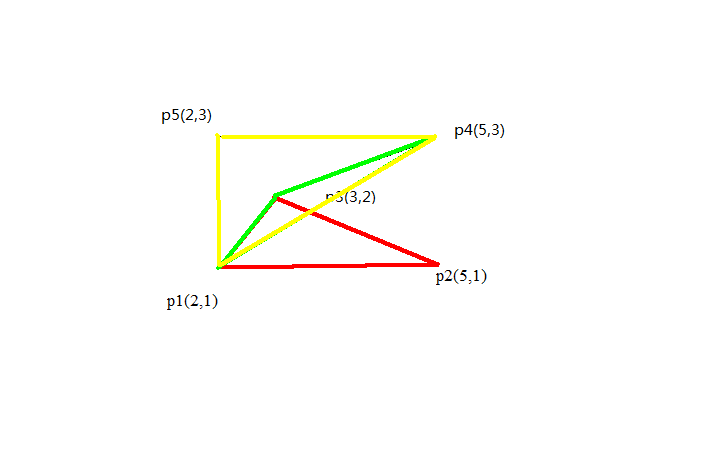
最後附上程式碼
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
struct node
{
double x,y;
}a[11000];
int i,j,k,m,n,o,p,js,jl;
double ans;
double multi(node p1,node p2, node p0)
{
double x1=p1.x-p0.x;
double y1=p1.y-p0.y;
double x2=p2.x-p0.x;
double y2=p2.y-p0.y;
return(x1*y2-x2*y1);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%lf%lf",&a[i].x,&a[i].y);
for(int i=2;i<=n;i++)
{
ans=ans+multi(a[i],a[i-1],a[1]);
}
ans=ans/2.0;
if(ans<0)ans=-ans;
printf("%0.4lf",ans);
return 0;
}
結語
通過上面的學習和例題,是不是已經初步了解了計算幾何的一點點精(皮)髓(毛)呢,希望你能有所收穫,在計算幾何的路上越走越遠吧(蒟蒻的我可能是走不下去了)
最後Orz各位大佬,寫的不好請各位神犇提出建議和意見,感謝你的閱讀:neckbeard:



