機器怎樣可以學得更好？

本系列是台灣大學資訊工程系林軒田（Hsuan-Tien Lin）教授開設的《機器學習基石》課程的梳理。重在梳理，而非詳細的筆記，因此可能會略去一些細節。

該課程共16講，分為4個部分：

機器什麼時候能夠學習？（When Can Machines Learn？）
機器為什麼能夠學習？（Why Can Machines Learn？）
機器怎樣學習？（How Can Machines Learn？）
機器怎樣可以學得更好？（How Can Machines Learn Better？）

本文是第4部分，對應原課程中的13-16講。

本部分的主要內容：

過擬合問題，過擬合與雜訊、目標函數複雜度的關係；
正則化，正則化與VC理論的聯繫；
驗證，留一交叉驗證和V-折交叉驗證；
三個學習原則，即奧卡姆剃刀、抽樣偏差和數據窺探。

1 過擬合問題

1.1 過擬合的發生

假設現在用帶很小雜訊的2次多項式生成了5個樣本，對於這5個樣本，其實用4次多項式就可以完美擬合它：

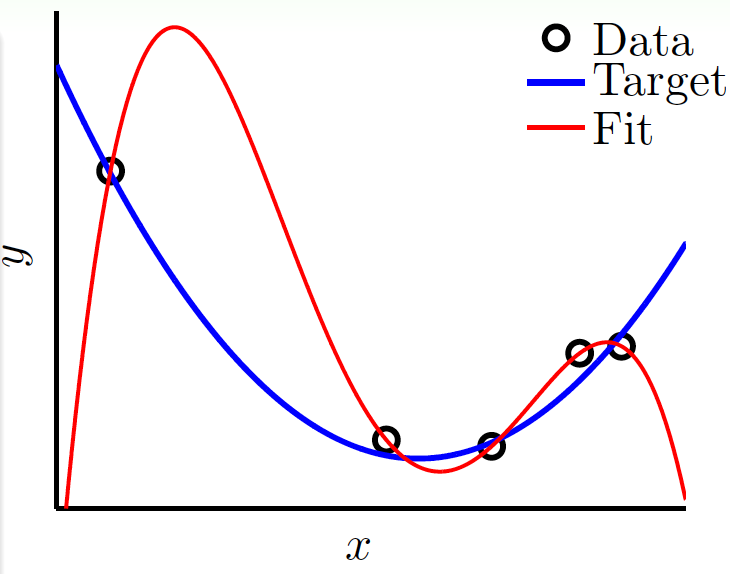
這樣做可使\(E_\text{in}=0\)，但\(E_\text{out}\)卻會非常大。

如果出現\(E_\text{in}\)很小，\(E_\text{out}\)很大的情況，就是出現了不好的泛化（bad generalization）。如果在訓練的過程中，\(E_\text{in}\)越來越小，\(E_\text{out}\)越來越大，就稱為過擬合（overfitting）。

雜訊和數據規模都會影響過擬合。先來看以下兩個數據集：

數據由10次多項式生成，有一些雜訊；
數據由50次多項式生成，無雜訊。

數據集影像如下：

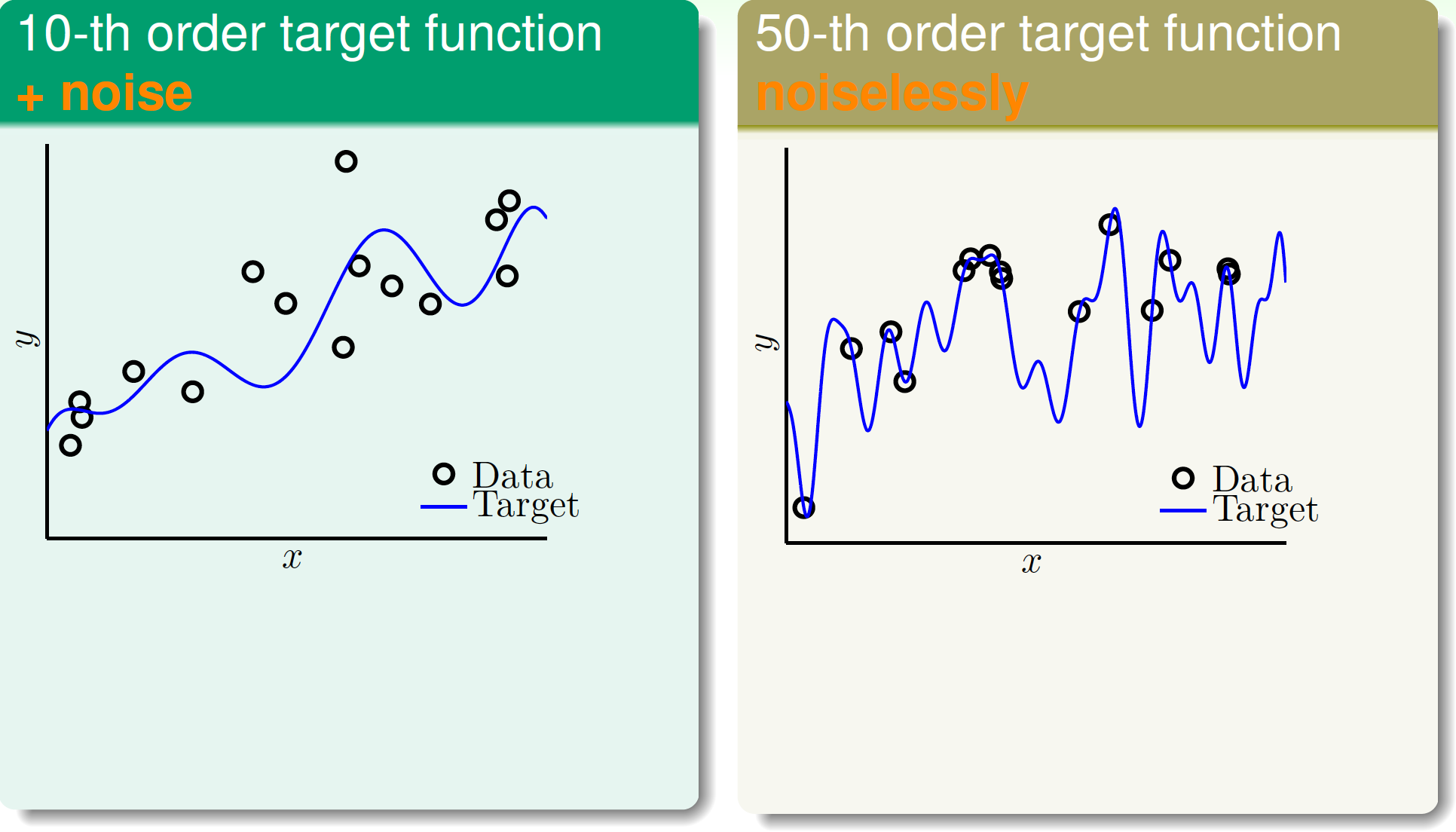
如果我們用2次和10次多項式分別擬合以上兩個數據集，那麼在從\(g_2 \in \mathcal{H}_2\)到\(g_{10} \in \mathcal{H}_{10}\)的過程中，會發生過擬合嗎？

擬合結果如下：

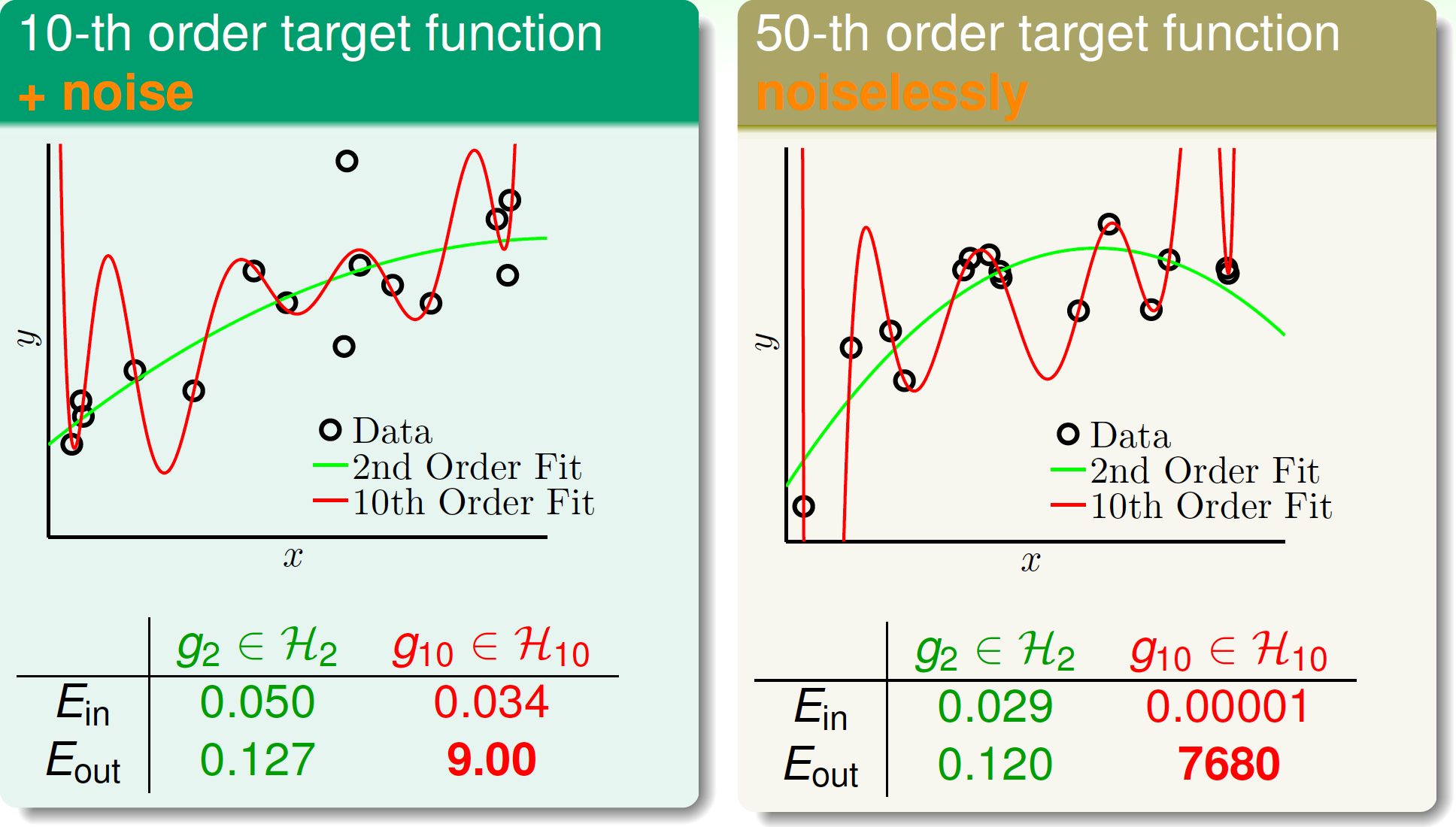
比較後發現，在兩個數據集中，都發生了過擬合！

來看學習曲線，當\(N\to \infty\)時顯然\(\mathcal{H}_{10}\)會有更小的\(\overline{E_{out}}\)，但\(N\)較小時它會有很大的泛化誤差。灰色區域就是過擬合發生的區域。

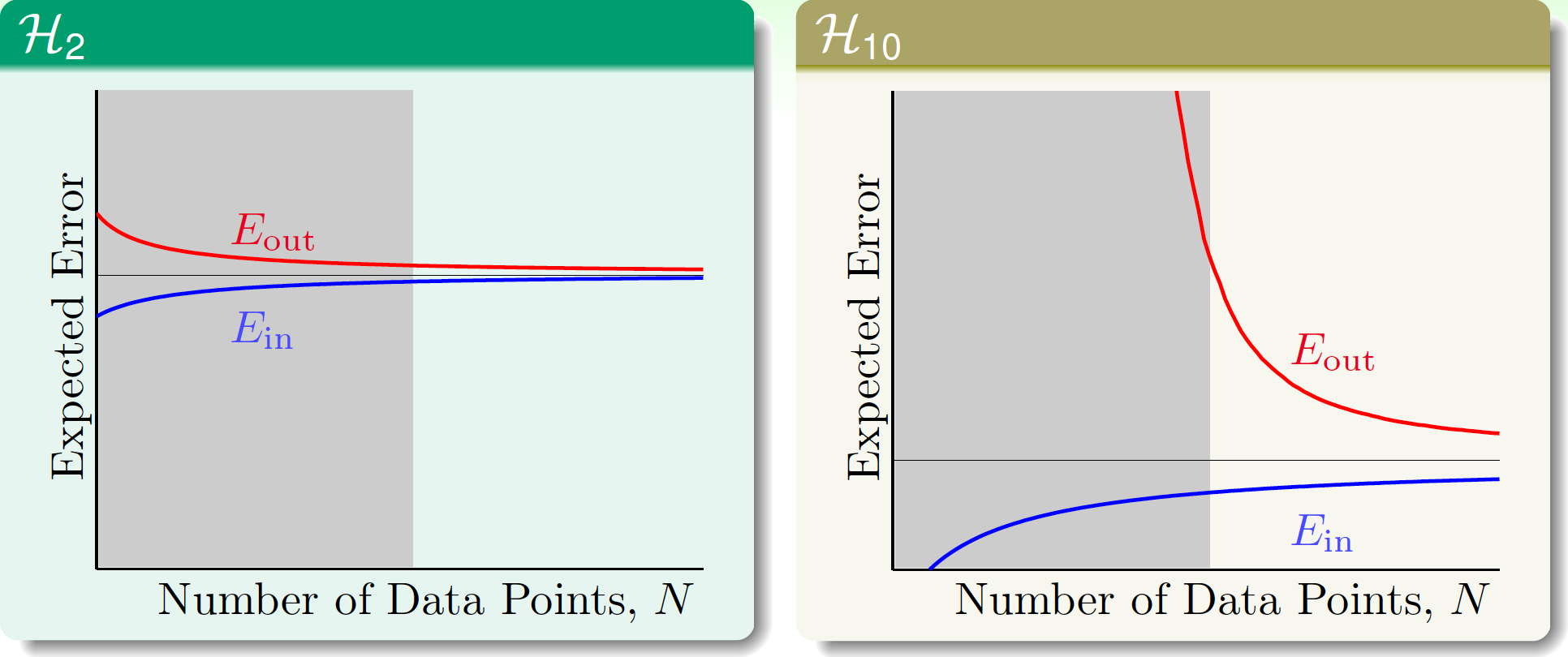
其實對於由無雜訊的50次多項式生成的數據，「目標函數的複雜度」本身就可以看作類似的雜訊。

接下來做個更細節的實驗。用

\[\begin{aligned}
y &= f(x) + \epsilon\\
&\sim \text{Gaussian}\left(\sum_{q=0}^{Q_f} \alpha_q x^q, \sigma^2 \right)
\end{aligned}
\]

生成\(N\)個數據，其中\(\epsilon\)是獨立同分布的高斯雜訊，雜訊水平為\(\sigma^2\)，\(f(x)\)關於複雜度水平\(Q_f\)是均勻分布的。也就是說，目標函數有\(Q_f\)和\(\sigma^2\)兩個變數。

然後，分別固定\(Q_f=20\)和\(\sigma^2=0.1\)，還是分別用2次和10次多項式擬合數據，並用\(E_\text{out}(g_{10})-E_\text{out}(g_{2})\)度量過擬合水平。結果如下：

顏色偏紅的區域，就是發生了過擬合。

加上去的\(\sigma^2\)高斯雜訊可稱為stochastic noise，而目標函數的次數\(Q_f\)也有類似雜訊的影響，因此可叫deterministic noise。

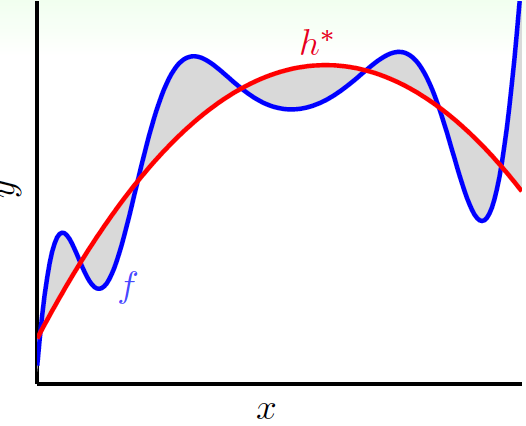
如果\(f\notin \mathcal{H}\)，那麼\(f\)一定有某些部分就無法被\(\mathcal{H}\)所捕捉到，最好的\(h^*\in\mathcal{H}\)與\(f\)的差就是deterministic noise，它的表現與隨機雜訊沒什麼不一樣（與偽隨機數生成器類似）。它與stochastic noise的不同之處在於，它與\(\mathcal{H}\)有關，且對於每個\(x\)，它的值是確定的：

1.2 過擬合的處理

一般來說，處理過擬合的思路有以下幾種：

從簡單的模型開始；
數據清洗（data cleaning），將錯誤的數據修正（如更正它的標籤類別）；
數據剪枝（data pruning），刪去離群點（outlier）；
data hinting，當樣本量不夠時，可以對現有樣本做些簡單的處理，增加樣本量，如在數字分類中，可以將數據微微旋轉或平移而不改變它們的標籤，這樣就可增大樣本量；
正則化（regularization），見下節；
驗證（validation），見後文。

2 正則化（regularization）

2.1 正則化

正則化的思想是好比從\(\mathcal{H}_{10}\)「逐步回退」到\(\mathcal{H}_{2}\)。這個名字的由來是在早期做函數逼近（function approximation）時，有很多問題是ill-posed problems，即有很多函數都是滿足問題的解，所以要加入一些限制條件。從某種意義上說，機器學習中的過擬合也是「正確的解太多」的問題。

\(\mathcal{H}_{10}\)中假設的一般形式為

\[w_0+w_1 x+w_2 x^2+w_3 x^3+\cdots+w_{10} x^{10}
\]

而\(\mathcal{H}_{2}\)中假設的一般形式為

\[w_0+w_1 x+w_2 x^2
\]

其實只要限制\(w_3=w_4=\cdots=w_{10}=0\)，就會有\(\mathcal{H}_{10}=\mathcal{H}_{2}\)。如果在用\(\mathcal{H}_{10}\)時加上這個限制，其實就是在用\(\mathcal{H}_2\)做機器學習。

\(\mathcal{H}_2\)的靈活性有限，但\(\mathcal{H}_{10}\)又很危險，那有沒有折中一些的假設集呢？不妨把這個條件放鬆一些，變成\(\sum\limits_{q=0}^{10}\mathbf{1}_{[w_1\ne 0]}\le 3\)，記在該限制下的假設集為\(\mathcal{H}_2’\)，有\(\mathcal{H}_{2}\subset \mathcal{H}_{2}’ \subset \mathcal{H}_{10}\)，即它比\(\mathcal{H}_{2}\)更靈活，但又沒有\(\mathcal{H}_{10}\)那麼危險。

在\(\mathcal{H}_{2}’\)下，求解的問題轉化成了

\[\min\limits_{\mathbf{w}\in \mathbb{R}^{10+1}} E_\text{in}(\mathbf{w})\quad \text{s.t. } \sum\limits_{q=0}^{10}\mathbf{1}_{[w_1\ne 0]}\le 3
\]

這是個NP-hard問題，複雜度很高。不如再將它變為

\[\min\limits_{\mathbf{w}\in \mathbb{R}^{10+1}} E_\text{in}(\mathbf{w})\quad \text{s.t. } \sum\limits_{q=0}^{10}w^2_q \le C
\]

記該假設集為\(\mathcal{H}(C)\)，它與\(\mathcal{H}_2’\)是有部分重疊的，並且對於\(C\)有軟的、光滑的結構：

\[\mathcal{H}_{0} \subset \mathcal{H}_{1} \subset \cdots \subset \mathcal{H}_{\infty} =\mathcal{H}_{10}
\]

記在\(\mathcal{H}(C)\)下找到的最優解為\(\mathbf{w}_\text{REG}\)。

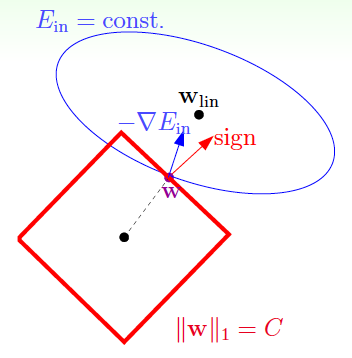
在沒有正則化時，用梯度下降更新參數的方向是\(-\nabla E_\text{in}(\mathbf{w})\)。而在加入了正則化\(\mathbf{w}^T \mathbf{w}\le C\)的限制時，必須在該限制下更新，如下圖：

\(\mathbf{w}^T \mathbf{w}= C\)的法向量（normal vector）就是\(\mathbf{w}\)，從圖中可知，只要\(-\nabla E_\text{in}(\mathbf{w})\)和\(\mathbf{w}\)不平行，就可繼續在該限制下降低\(E_\text{in}(\mathbf{w})\)，因此，達到最優解時，一定有

\[-\nabla E_\text{in}(\mathbf{w}) \propto \mathbf{w}_\text{REG}
\]

由此，問題可以轉化為求解

\[\nabla E_\text{in}(\mathbf{w}_\text{REG}) +\dfrac{2 \lambda}{N} \mathbf{w}_\text{REG}=0
\]

其中\(\lambda\)是引入的拉格朗日乘子（Lagrange multiplier）。假設已知\(\lambda>0\)，只需要把梯度的式子寫出來，即有：

\[\dfrac{2}{N}(X^T X\mathbf{w}_\text{REG}-X^T \mathbf{y})+\dfrac{2 \lambda}{N} \mathbf{w}_\text{REG}=0
\]

直接求解即可得

\[\mathbf{w}_\text{REG}\leftarrow (X^T X+\lambda I)^{-1} X^T\mathbf{y}
\]

只要\(\lambda>0\)，\(X^T X+\lambda I\)就是正定矩陣，它一定可逆。

在統計學中，這通常叫嶺回歸（ridge regression）。

換一種視角來看，求解

\[\nabla E_\text{in}(\mathbf{w}_\text{REG}) +\dfrac{2 \lambda}{N} \mathbf{w}_\text{REG}=0
\]

就等價於求解（相當於對上式兩邊取積分）

\[\min\limits_{\mathbf{w}} E_\text{in}(\mathbf{w})+\dfrac{\lambda}{N}\mathbf{w}^T\mathbf{w}
\]

\(\mathbf{w}^T\mathbf{w}\)可叫regularizer，整個\(E_\text{in}(\mathbf{w})+\dfrac{\lambda}{N}\mathbf{w}^T\mathbf{w}\)可叫作augmented error \(E_\text{aug}(\mathbf{w})\)。

這樣，原本是給定\(C\)後解一個條件最值問題，現在轉化成了一個給定\(\lambda\)的無條件最值問題。

可將\(+\dfrac{\lambda}{N}\mathbf{w}^T\mathbf{w}\)稱為weight-decay regulariztion，因為更大的\(\lambda\)，就相當於讓\(\mathbf{w}\)更短一些，也相當於\(C\)更小一點。

一個小細節：在做特徵變換時，如果用\(\Phi(\mathbf{x})=(1,x,x^2,\ldots,x^Q)\)，假設\(x_n \in [-1,+1]\)，那麼\(x^q_n\)會非常小，這一項本來就需要很大的\(w_q\)才能起到作用，如果此時再用正則化，就對高維的係數有些「過度懲罰」了，因為它本來就要比較大才行。因此，可在多項式的空間中找出一些正交的基函數（orthonormal basis function），這是一些比較特別的多項式，叫勒讓德多項式（Legendre Polynomials），再用這些多項式這樣做特徵變換\((1,L_1(x),L_2(x),\ldots,L_Q(x))\)即可。前5個勒讓德多項式如下圖：

2.2 正則化與VC理論

在最小化augmented error的時候，儘管它與帶約束最值問題是等價的，但在計算時，其實並沒有真正的將\(\mathbf{w}\)限制在\(\mathcal{H}(C)\)中。那麼正則化究竟是怎麼發生的？

可以從另一個角度看augmented error：

\[E_\text{aug}(\mathbf{w})=E_\text{in}(\mathbf{w})+\dfrac{\lambda}{N}\mathbf{w}^T\mathbf{w}
\]

若記\(\mathbf{w}^T\mathbf{w}\)為\(\Omega(\mathbf{w})\)，它度量的是某個假設\(\mathbf{w}\)的複雜度。而在VC Bound中

\[E_\text{out}(\mathbf{w})\le E_\text{in}(\mathbf{w})+\Omega(\mathcal{H})
\]

\(\Omega(\mathcal{H})\)度量的是整個\(\mathcal{H}\)的複雜度。如果\(\dfrac{\lambda}{N}\Omega(\mathbf{w})\)與\(\Omega(\mathcal{H})\)有某種關聯，\(E_\text{aug}\)就可以直接作為\(E_\text{out}\)的代理，不需要再通過做好\(E_\text{in}\)來做好\(E_\text{out}\)，而同時，又可以享受整個\(\mathcal{H}\)的高度靈活性。

再換個角度，原本對於整個\(\mathcal{H}\)有\(d_\text{VC}(\mathcal{H})=\tilde{d}+1\)，而現在相當於只考慮\(\mathcal{H}(C)\)中的假設，也就是說VC維變成了\(d_\text{VC}(\mathcal{H}(C))\)。可以定義一個「有效VC維」\(d_\text{EFF}(\mathcal{H},\mathcal{A})\)，只要\(\mathcal{A}\)中做了正則化，有效VC維就會比較小。

2.3 更一般的正則項

有沒有更一般的正則項\(\Omega(\mathbf{w})\)？該如何選擇呢？有以下建議：

與目標有關（target-dependent），如果知道目標函數的一些性質，就可以寫出來，比如我們預先知道目標函數是接近於偶函數的，那就可以選取\(\sum \mathbf{1}_{[q \text{ is odd}]} w^2_q\)；
合理的（plausible），可以選平滑的或簡單的，如為了稀疏性而選L1正則項\(\sum\vert w_q \vert\)，下文會說明；
友好的（friendly），即容易優化，如L2正則項\(\sum w_q^2\)；
就算選的正則項不好，也沒有關係，因為可以靠\(\lambda\)來調節，最差也就是相當於沒有加入正則項。

L1正則項如下圖：

它是凸的，但不是處處可微，加入它之後，解具有稀疏性。如果在實際中需要有稀疏解，L1就會很有用。

\(\lambda\)要怎麼選呢？可根據\(E_\text{out}\)的情況選出的最優\(\lambda\)，示例如下（加粗點為最優\(\lambda\)）：

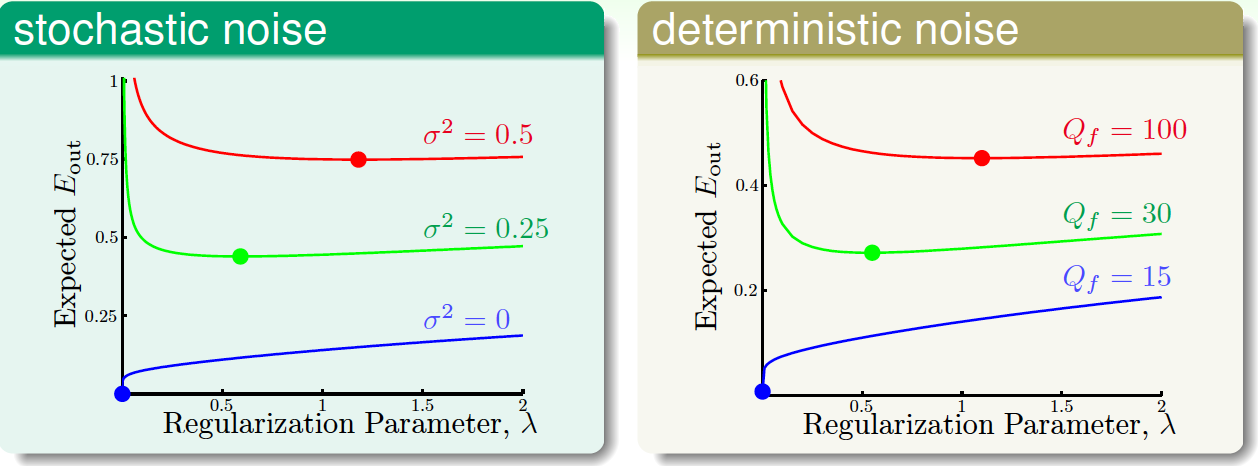
從圖中可以看到，雜訊越大，越需要增加regularization。

但一般情況下，雜訊是未知的，該如何選擇合適的\(\lambda\)？

3 驗證（Validation）

3.1 驗證集

\(\lambda\)該如何選擇？我們完全不知道\(E_\text{out}\)，並且也不能直接通過\(E_\text{in}\)做選擇。如果有一個從來沒被使用過的測試集就好了，這樣就可以根據測試集進行選擇：

\[m^*=\mathop{\arg\min}\limits_{1\le m\le M} \left( E_m=E_\text{test}(\mathcal{A}_m(\mathcal{D})) \right)
\]

並且，這樣做是有泛化保證的（Hoeffding）：

\[E_\text{out}(g_{m^*})\le E_\text{test}(g_{m^*})+O(\sqrt{\dfrac{\log M}{N_\text{test}}})
\]

但哪裡有真正測試集？只能折中地從\(\mathcal{D}\)劃分出一部分數據作為驗證集\(\mathcal{D}_\text{val}\subset \mathcal{D}\)了，當然，也要求它是在過去從未被\(\mathcal{A}_m\)使用過的。

劃分驗證集\(\mathcal{D}_\text{val}\)的過程如下：

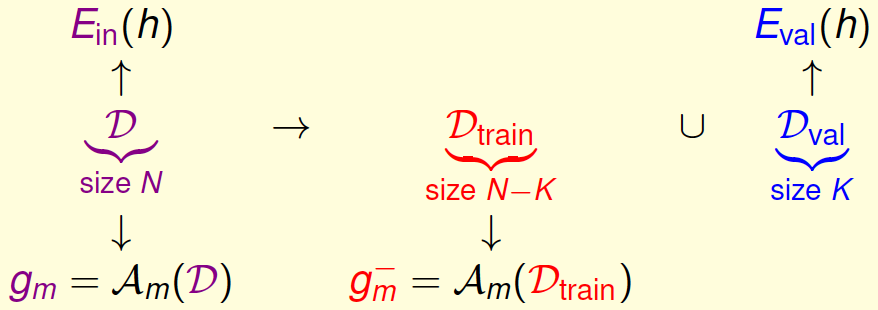
用訓練集得到的\(g^-_m\)，也可以有泛化保證：

\[E_\text{out}(g_m^-)\le E_\text{val}(g_m^-)+O(\sqrt{\dfrac{\log M}{K}})
\]

做驗證時的一般流程如下：

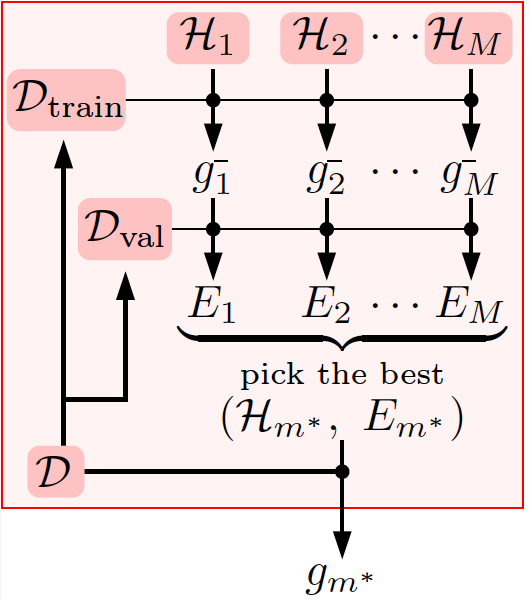
可以看到，在用驗證集選出最好的模型\(g^-_{m^*}\)後，還是要用所有的數據再訓練一個最好的模型\(g_{m^*}\)出來，一般來說這次訓練得到的\(g_m^*\)會由於訓練數據量的更大而有更低的\(E_\text{out}\)，見下圖：

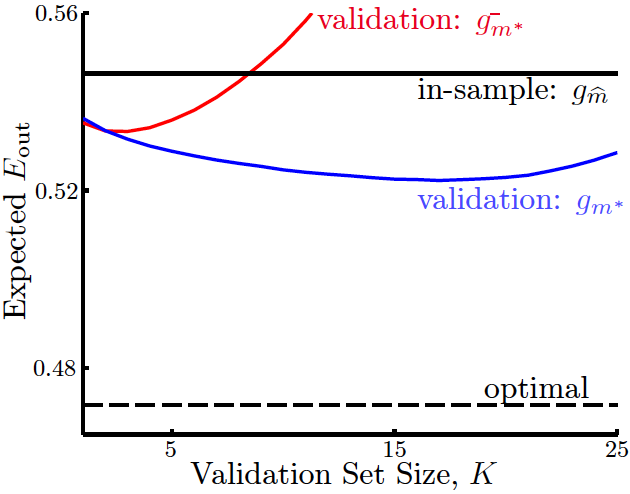
圖中最下面的虛線為\(E_\text{out}\)。可以看到，\(K\)不能過大或過小，如果\(K\)過小，雖然\(g_m^-\approx g_m\)，但\(E_\text{val}\)和\(E_\text{out}\)會差別很大，而如果\(K\)過大，儘管\(E_\text{val}\approx E_\text{out}\)，但會使\(g_m^-\)比\(g_m\)差很多。

我們真正想要做到的是

\[E_\text{out}(g)\approx E_\text{out}(g^-)\approx E_\text{val}(g^-)
\]

第一個約等號要求\(K\)較小，第二個約等號要求\(K\)較大，因此必須選一個合適的\(K\)，按經驗法則可選\(K=\dfrac{N}{5}\)。

3.2 留一交叉驗證（LOOCV）

如果讓\(K=1\)，即只留一個樣本\(n\)作為驗證集，記

\[E_\text{val}^{(n)}(g_n^-)=\text{err}(g_n^-(\mathbf{x}_n),y_n)=e_n
\]

但單個\(e_n\)無法告訴我們準確的資訊，要想辦法對所有可能的\(E_\text{val}^{(n)}(g_n^-)\)取平均。可以用留一交叉驗證（Leave-One-Out Cross Validation）：

\[E_\text{loocv}(\mathcal{H},\mathcal{A})=\dfrac{1}{N}\sum\limits_{n=1}^{N} e_n=\dfrac{1}{N} \sum\limits_{n=1}^{N} \text{err}(g_n^- (\mathbf{x}_n),y_n)
\]

我們希望的是有\(E_\text{loocv}(\mathcal{H},\mathcal{A})\approx E_\text{out}(g)\)。可作證明：

\[\begin{aligned}
&\mathop{\mathcal{E}}\limits_{\mathcal{D}} E_\text{loovc}(\mathcal{H},\mathcal{A})\\ =& \mathop{\mathcal{E}}\limits_{\mathcal{D}}\dfrac{1}{N}\sum\limits_{n=1}^{N} e_n\\
=&\dfrac{1}{N} \sum\limits_{n=1}^{N} \mathop{\mathcal{E}}\limits_{\mathcal{D}} e_n\\
=&\dfrac{1}{N} \sum\limits_{n=1}^{N} \mathop{\mathcal{E}}\limits_{\mathcal{D}_n} \mathop{\mathcal{E}}\limits_{(\mathbf{x}_n,y_n)} \text{err}(g_n^-(\mathbf{x}_n),y_n)\\
=&\dfrac{1}{N} \sum\limits_{n=1}^{N} \mathop{\mathcal{E}}\limits_{\mathcal{D}_n} E_\text{out}(g_n^-)\\
=&\dfrac{1}{N} \sum\limits_{n=1}^{N} \overline{E_\text{out}}(N-1)\\
=& \overline{E_\text{out}}(N-1)
\end{aligned}
\]

由於\(E_\text{loovc}(\mathcal{H},\mathcal{A})\)的期望會告訴我們一些關於\(E_\text{out}(g^-)\)的期望的資訊，因此也叫作\(E_\text{out}(g)\)的「幾乎無偏估計」（almost unbiased estimate）。

用手寫數字識別——對數字是否為1進行分類——看看效果，兩個基礎特徵為對稱性和平均強度（average intensity），對它們進行特徵變換（增加特徵數量），再分別用\(E_\text{in}\)和\(E_\text{loocv}\)進行參數選擇（參數是變換後的特徵個數），結果如下：

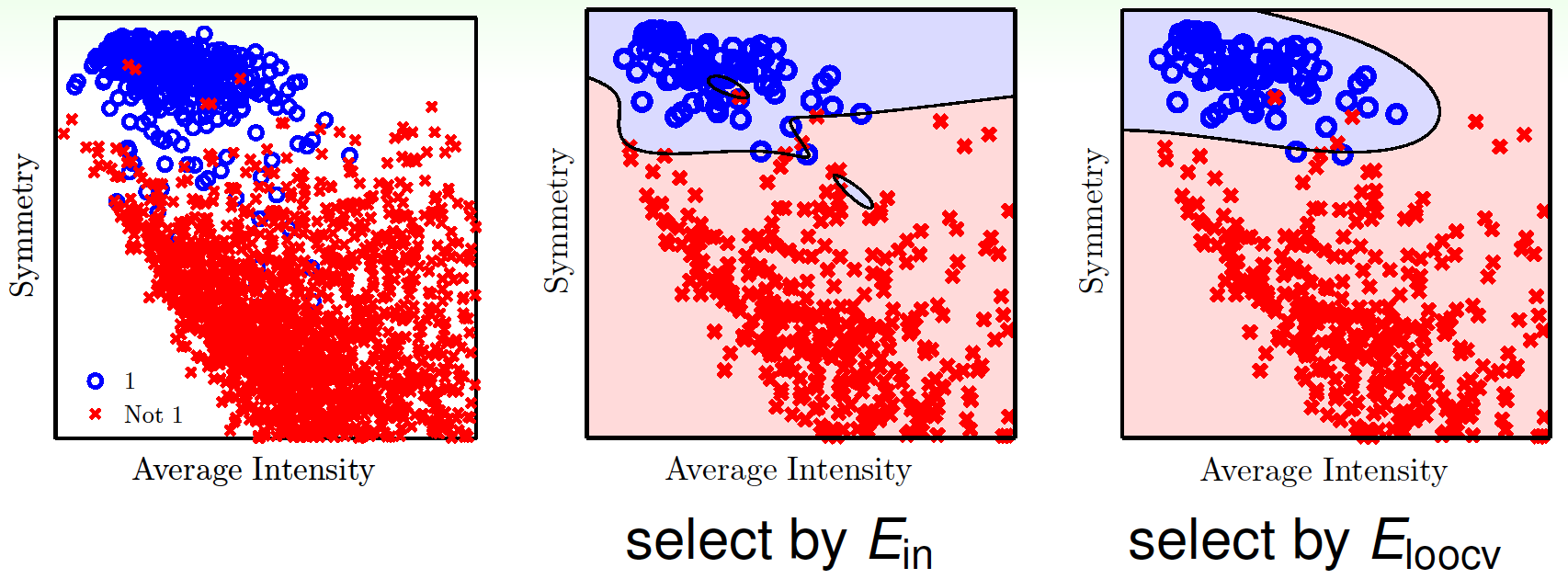
如果將\(E_\text{out}\)、\(E_\text{in}\)、\(E_\text{loocv}\)分別隨特徵數變化而變化的情況畫出來，如圖：

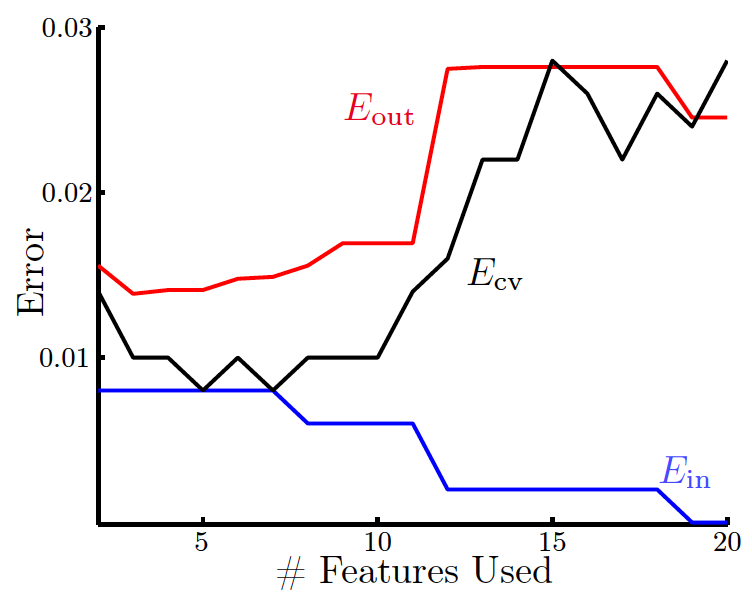
3.3 \(V\)-折交叉驗證

如果有1000個點，做留一交叉驗證就要計算1000次\(e_n\)，每次計算還要用999個樣本做訓練，除了少數演算法（如線性回歸，它有解析解），在大多數情況下會非常耗時間。另一方面，由上一節最後可看到，由於\(E_\text{loocv}\)是在單個點上做平均，結果會有跳動，不夠穩定。因此，在實際中，loocv並不是很常用。

在實際中，更常用的是\(V\)折交叉驗證（\(V\)-Fold Cross Validation），即將\(\mathcal{D}\)隨機分為\(V\)等分，輪流用每一份做驗證，用剩下的\(V-1\)份做訓練，在實際中一般常取\(V=10\)，如下圖：

這樣能計算出

\[E_\text{cv}(\mathcal{H}, \mathcal{A})=\dfrac{1}{V}\sum\limits_{v=1}^{V} E_\text{val}^{(v)}(g_v^-)
\]

再用它對參數做選擇：

\[m^*=\mathop{\arg\min}\limits_{1\le m\le M} \left( E_m=E_\text{cv}(\mathcal{H}_m, \mathcal{A}_m) \right)
\]

值得注意的是，由於驗證過程也是在做選擇，它的結果依舊會比最後的測試結果樂觀一些。因此，最後重要的是測試的結果，而非找出來的最好的驗證的結果。

4 三個學習的原則

這裡介紹三個學習的原則。

4.1 奧卡姆剃刀

首先是奧卡姆剃刀（Occam’s Razor）。

An explanation of the data should be made as simple as possible, but no simpler.

–Albert Einsterin (?)

這句話傳說是愛因斯坦所說，但沒有證據。最早可追溯到奧卡姆的話：

entia non sunt multiplicanda praeter necessitatem (entities must not be multiplied beyond necessity)

–William of Occam (1287-1347)

在機器學習中，這是說能擬合數據的最簡單的模型往往是最合理的。

什麼叫簡單的模型呢？對於單個假設\(h\)來說，要求\(\Omega(h)\)較小即參數較少，對於一個模型（假設集）\(\mathcal{H}\)來說，要求\(\Omega(\mathcal{H})\)較小即它沒包含太多可能的假設。這兩者是相關的，比如\(\vert \mathcal{H} \vert\)規模是\(2^\ell\)，那麼其實只需要\(\ell\)個參數就可以描述所有的\(h\)，因此小的\(\Omega(\mathcal{H})\)也就意味著小的\(\Omega(h)\)。

從哲學意義上說，越簡單的模型，「擬合」發生的概率越小，如果真的發生了，那就說明數據中可能真的有一些比較重要的規律。

4.2 抽樣偏差

第二個是要注意抽樣偏差（Sampling Bias）。

如果數據的抽樣過程存在偏差，那麼機器學習也會產生一個有偏差的結果。

在講解VC維時，提到過一個前提條件，就是訓練數據和測試數據需要來自同一個分布。當無法滿足時，經驗法則是，儘可能讓測試環境和訓練環境儘可能匹配。

4.3 數據窺探

第三是要注意數據窺探（Data Snooping）。

如果你通過觀察，發現數據比較符合某個模型，進而選用該模型，這是比較危險的，因為相當於加入了你大腦中的模型的複雜度。

在任何使用數據的過程中，其實都是間接窺探到了數據。在窺探了數據的表現後，做任何決策，都會引入「大腦」複雜度。

比如在做scaling時，不能把訓練集和測試集放在一起做scaling，而只能對訓練集做。

其實在機器學習的前沿研究中，也存在類似的情況。比如第一篇論文發現了\(\mathcal{H}_1\)會在\(\mathcal{D}\)上表現較好，而第二篇論文提出了\(\mathcal{H}_2\)，它在\(\mathcal{D}\)上比\(\mathcal{H}_1\)表現得更好（否則就不會發表），第三篇也如此……如果將所有論文看作一篇最終版的論文，那麼真正的VC維其實是\(d_\text{vc}(\cup_m \mathcal{H}_m)\)，它會非常大，泛化會非常差。這是因為其實在每一步過程中，作者都通過閱讀前人的文獻而窺探了數據。

因此在做機器學習時，要審慎地處理數據。要避免用數據來做一些決策，即最好事先就將領域知識加入到模型中，而不是在觀察了數據後再把一些特性加入模型中。另外，無論是在實際操作中，還是在看論文過程中，或者是在對待自己的結果時，都要時刻保持懷疑。

Tags: 人工智慧十年劍數據挖掘機器學習過擬合