淺談棧和隊列
- 2019 年 10 月 31 日
- 筆記
### 棧
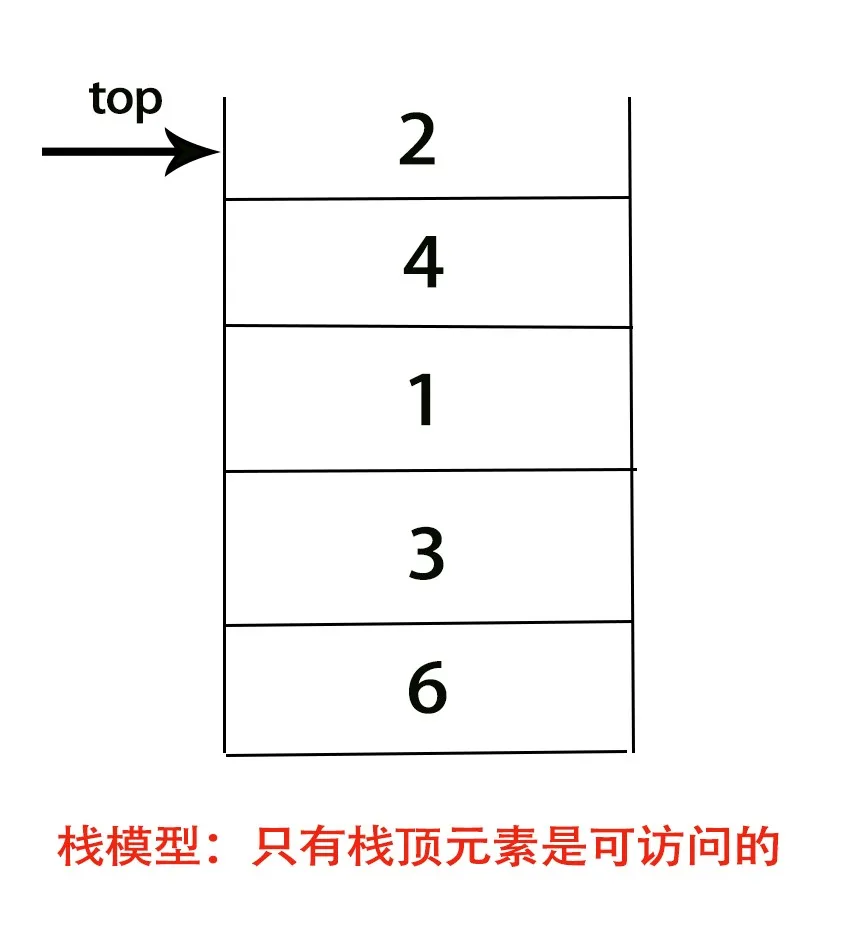
棧模型
棧(stack)是限制對元素的插入(push)和刪除(pop)只能在一個位置上進行的表,該位置是表的末端,叫做棧的棧頂(top)。
棧的基本操作只有兩種,壓入棧(push)和彈出棧頂(pop),且只能作用於棧頂。(只有棧頂元素是可訪問的

你可以把棧結構理解成一個底部封閉,頂部打開的桶。最先進去的元素一定是最後才能取出,最晚進去的元素一定是最先取出。
因此棧又叫做LIFO(後進先出,Last In First Out)表。

棧的優勢
棧的操作是常數時間的,而且是以非常快的常數時間。在某些機器上,push和pop都可以寫成一條機器指令,現代電腦把棧操作作為它指令的一部分。因此棧是在電腦科學中繼數組之後最基本的數據結構。
棧的實現
棧的實現分為數組實現和鏈表實現。
1` 鏈表實現
這裡我們使用單鏈表來實現,定義一個first指針指向棧頂,棧的鏈表實現實際上是簡化了單鏈表實現,具體實現看以下程式碼。
public class StackImplementByLinklist<AnyType> { public Node<AnyType> first; int size; //內部類定義node public class Node<AnyType>{ AnyType data; Node<AnyType> next; } //初始化 public void stack(){ first=null; size=0; } public void push(AnyType a){ Node oldNode=first; first=new Node(); first.data=a; first.next=oldNode; size++; } public AnyType pop(){ AnyType a=first.data; first=first.next; size--; return a; } public boolean isEmpty(){ return size==0; } public int size(){ return size; } } 2` 數組實現
相比於鏈表實現,數組實現棧更加的常用。因為數組操作的常數時間極短,而且實現起來更加簡單。
public class StackImplementByArray<AnyType> { AnyType[] arr; int size; public void stack(int capacity){ arr=(AnyType[])new Object[capacity]; size=0; } public void push(AnyType a){ if(size==arr.length){ changeArray(2*size+1); } arr[size]=a; size++; } public AnyType pop(){ if(size==0){ System.out.println("棧頂為空"); System.exit(0); } AnyType a=arr[size-1]; arr[size-1]=null; size--; return a; } public boolean isEmpty(){ return size==0; } public int size(){ return size; } //由於數組大小是要先確定的,因此當數組滿了後要擴大數組容量 public void changeArray(int newCapacity){ AnyType[] newArr=(AnyType[])new Object[newCapacity]; for(int i=0;i<arr.length;i++){ newArr[i]=arr[i]; } arr=newArr; } } 棧的應用
-
平衡符號的檢測
編譯器檢查程式符號的語法錯誤,常常就是通過棧來實現的。
在編程時,我們經常會用到「 ( ),[ ],{ }," " 」這些符號,當這些符號不是配對出現的,編譯器就會報錯,編譯就無法通過。
那麼,編譯器是怎麼知道這些符號有沒有配對出現的呢?它通常是這麼處理的。
當遇到左符號,如「( [ { " 」這些,就把它壓入一個準備好的棧;否則就彈出棧頂,檢測當前符號是否與棧頂元素配對。一旦不能配對,直接退出報錯。
-
算術表達式的求值
### 隊列
隊列模型
wiki: 隊列,又稱為佇列(queue),是先進先出(FIFO, First-In-First-Out)的線性表。在具體應用中通常用鏈表或者數組來實現。隊列只允許在後端(稱為rear)進行插入操作,在前端(稱為front)進行刪除操作。隊列的操作方式和堆棧類似,唯一的區別在於隊列只允許新數據在後端進行添加。
隊列模型就相當於我們日常生活的排隊,在隊伍的後面入隊,在隊伍的前端出隊。

多種隊列
隊列一般分為普通的數組隊列,鏈表隊列和循環隊列。
鏈表隊列:長度一般是無限的,一般不存在溢出的可能性,用完就銷毀,不會浪費記憶體空間。
普通的數組隊列:長度一般是有限的,即數組長度。由於元素出隊後其位置的記憶體空間並不會釋放,因此會浪費大量的記憶體空間。
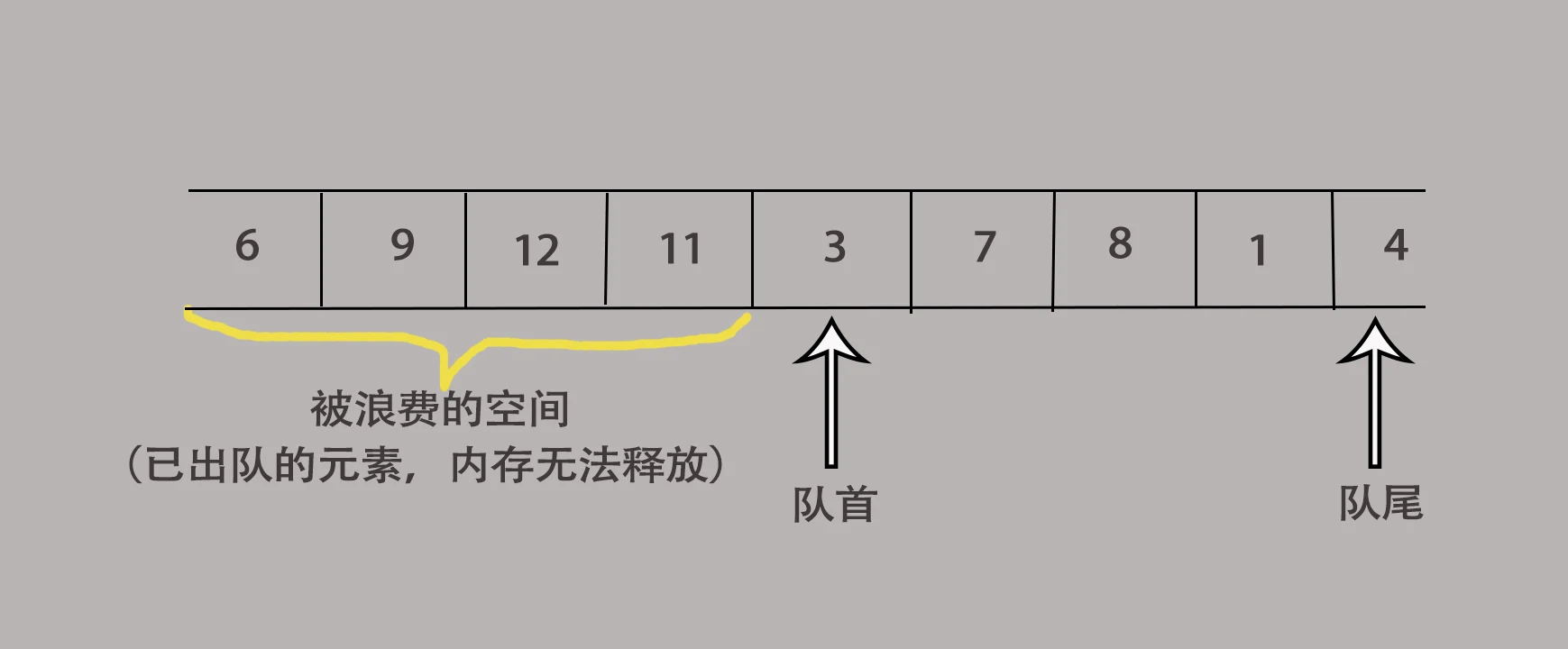
循環隊列:特殊的數組隊列,由於普通的數組的隊列會浪費大量的記憶體空間,因此出現了循環隊列。當循環隊列的隊尾指針到達數組末尾後,會重新回到數組起始位置,實現了對記憶體的重複利用。

隊列的實現
1` 鏈表隊列
public class QueueImplementByLinkList<AnyType> { Node first;//隊首 Node last;//隊尾 int size; public class Node{ AnyType data; Node next; public Node(AnyType data,Node next){ this.data=data; this.next=next; } } //初始化隊列 public void initqueue(){ first=new Node(null,null); last=first; size=0; } //入隊 public void enqueue(AnyType a){ if(size==0){ last.data=a; size++; return; } Node oldlast=last; last=new Node(a,null); oldlast.next=last; size++; } //出隊 public AnyType dequeue(){ if(size==0){ System.out.print("隊列為空"); System.exit(0); } AnyType a=first.data; first=first.next; size--; return a; } public boolean isEmpty(){ return size==0; } public int size(){ return size; } } 2` 數組隊列
public class QueueImplementByArray<AnyType> { AnyType[] arr; int first; int last; int size; //初始化 public void ininqueue(int capacity){ arr=(AnyType[])new Object[capacity]; first=0; last=0; size=0; } public void enqueue(AnyType a){ if(size==arr.length){ changeArray(2*size+1); } arr[last++]=a; size++; } public AnyType dequeue(){ if(size==0){ System.out.println("隊列為空"); System.exit(0); } AnyType a=arr[first++]; arr[first-1]=null; size--; return a; } public void changeArray(int newCapacity){ AnyType[] newArr=(AnyType[])new Object[newCapacity]; for(int i=0;i<arr.length;i++){ newArr[i]=arr[i]; } arr=newArr; } public boolean isEmpty(){ return size==0; } public int size(){ return size; } } 3` 循環隊列
public class CycleQueue { int[] arr; int start;//隊首 int end;//隊尾 int size=0; //初始化 public void initqueue(int size){ arr=new int[size]; size=0; start=0; end=0; } //入隊 public void enqueue(int num){ if(size>arr.length){ System.out.println("隊列已滿"); return; } if(end==arr.length){ end=0; } arr[end++]=num; size++; } //出隊 public int dequeue(){ if(size==0){ System.out.println("隊列為空"); System.exit(0); } if(start==arr.length){ start=0; } size--; return arr[start++]; } public boolean isEmpty(){ return size==0; } public int size(){ return size; } } 一點點總結
棧和隊列是基本的數據結構,是對數組和鏈表的重新封裝和擴展。由於它們的特性和執行速度,棧和隊列被廣泛的使用。
最後,不要為了使用數據結構而使用使用數據結構,要區分各種數據結構的使用場景,靈活地運用數據結構,可以事半功倍。


