紅黑樹演算法原理（十三）

2019 年 10 月 31 日
筆記

前言

最近斷斷續續花了一個禮拜的時間去看紅黑樹演算法，關於此演算法還是比較難，因為涉及到諸多場景要考慮，同時接下來我們要講解的HashMap、TreeMap等原理都涉及到紅黑樹演算法，所以我們不得不了解其原理，關於一些基礎知識這裡不再講解，本文參考博文：《https://www.cnblogs.com/aspirant/p/9084199.html》，參考鏈接太多文字描述，看過很多關於紅黑樹的文章，有些越講越懵逼，有些講的挺好關鍵是不說人話（這裡不是罵人哈，指的是文章講解的還是有點抽象），在這裡希望通過我個人的理解既讓閱讀本文的您能夠充分理解其原理也能完全快速記住各種場景。

紅黑樹原理

紅黑樹是一種自平衡二進位搜索樹（BST），紅黑樹與AVL樹相比，AVL樹更加平衡，但是它們可能會在插入和刪除過程中引起更多旋轉。因此，如果我們的應用程式涉及許多頻繁的插入和刪除操作，則應首選紅黑樹。但是，如果插入和刪除操作的頻率較低，而搜索操作的頻率較高，則AVL樹應優先於紅黑樹。我們需牢記紅黑樹的每個節點所遵循的以下規則

（1）每個節點或者是黑色，或者是紅色。
（2）根節點是黑色。
（3）每個葉子節點是黑色。 [注意：這裡葉子節點，是指為空的葉子節點，在演算法原理中空用Nil表示，但是在面向對象語言中空都用NULL表示]
（4）如果一個節點是紅色的，則它的子節點必須是黑色的（注意：這裡指的是不能有兩個連續的紅色節點）。
（5）從一個節點到該節點的子孫節點的所有路徑上包含相同數目的黑節點。

了解如上規則後，接下來將進入紅黑樹的插入和刪除操作，插入操作還好，最複雜的在於刪除操作，莫慌，我們一步步來，無論是插入還是刪除操作都可能會引起樹的再次不平衡即會打破以上紅黑樹的規則，在進行插入或刪除操作時，為使得樹再次平衡我們使用【變色】和【旋轉】方法來解決。假如Z為插入節點，在這裡我們做如下命名約定：父親節點、祖父節點、叔叔節點。好了，接下來我們首先來看插入操作。

紅黑樹插入

一說到插入我們立馬就有了疑惑，根據紅黑樹規則一來看，每個節點非紅即黑，那麼我們插入的節點到底是紅色還是黑色呢？如果為黑色將很大可能性會破壞規則五，此時我們為使樹再次平衡將花費很大功夫，但是如果為紅色，也很有可能性破壞以上規則二和四，但是比插入節點為黑色更加易於修復。所以這就是為什麼插入節點為紅色的原因。所以第一步，我們執行標準的BST插入且節點顏色為紅色，插入操作分為以下四種場景。

（1）Z是根節點

（2）Z的父親為紅色節點、叔叔為紅色節點

（3）Z的父親為紅色節點、叔叔為黑色節點（直線）

（4）Z的父親為紅色節點、叔叔為黑色節點（三角形）

Z是根節點

當Z是根節點時，因為默認插入節點為紅色，但根據紅黑樹規則二根節點為黑色，所以進行變色，直接將紅色變為黑色，如下：

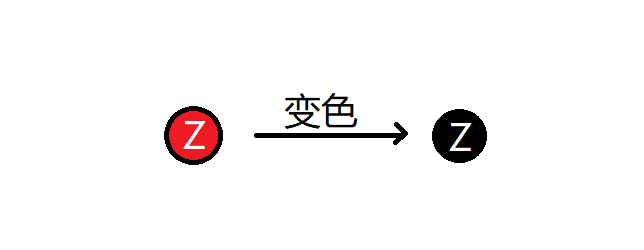
Z的父親為紅色節點、叔叔為紅色節點

不區分Z是在其父親節點左側或者右側，也不區分Z的父親節點是在Z的祖父節點左側或者右側都進行如下相同處理操作。

（1）將“父親節點”設為黑色。
（2）將“叔叔節點”設為黑色。
（3）將“祖父節點”設為“紅色”。
（4）將“祖父節點”設為“當前節點”(紅色節點)；即，之後繼續對“當前節點”進行操作。

或者

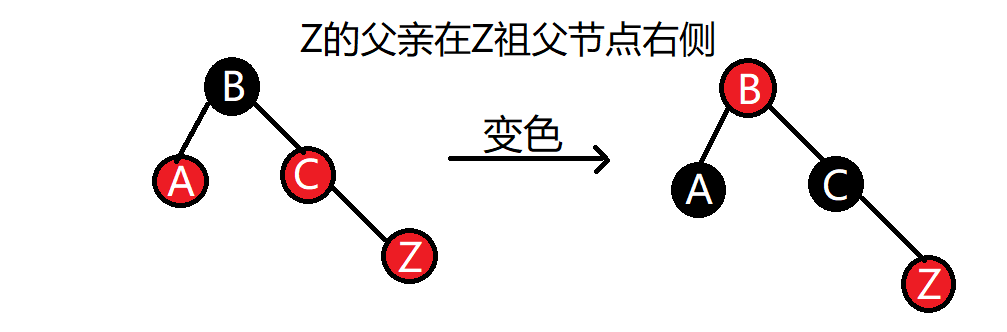
Z的父親為紅色節點、叔叔為黑色節點（直線）

根據如上大前提，有的童鞋可能分為Z在其父親節點左側和右側兩種情況，這裡我採用的是Z、Z的父親節點、Z的祖父節點在同一條直線上時的兩種對稱情況，同理如下講解三角形時也是一樣，將Z、Z的父親節點、Z的祖父節點構成三角形時的兩種對稱情況，這樣在腦海中思考並畫一筆是不是會更好理解一點呢。由於對稱分為兩種情況：

（1）當Z的父親節點在Z的祖父節點左側時：【1】將“父親節點”設置為黑色【2】將“祖父節點”設置為紅色【3】以“父親節點”右旋

（2）當Z的父親節點在Z的祖父節點右側時：【1】將“父親節點”設置為黑色【2】將“祖父節點”設置為紅色【3】以“祖父節點”左旋

或者

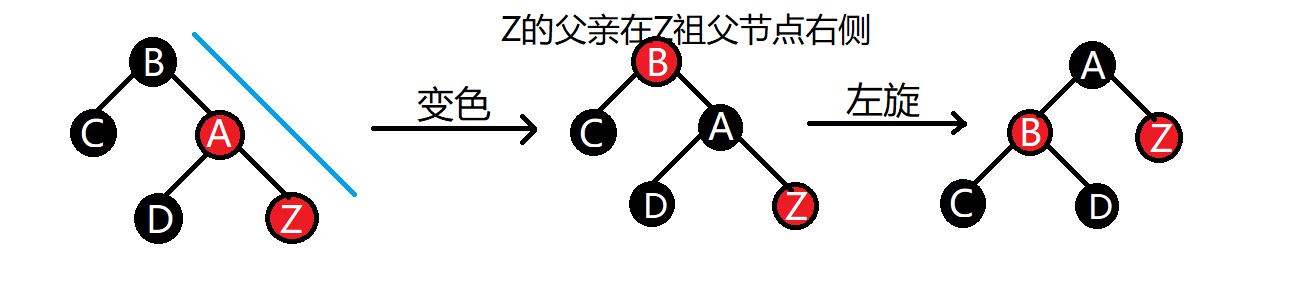
Z的父親為紅色節點、叔叔為黑色節點（三角形）

（1）當Z的父親節點在Z的祖父節點左側時：【1】將“父親節點”左旋【2】將“父親節點”設置為當前節點（即如下A節點）【3】演變為如上直線第1種情況，繼續操作

（2）當Z的父親節點在Z的祖父節點右側時：【1】將“父親節點”右旋【2】將“父親節點”設置為當前節點（即如下A節點）【3】演變為如上直線第2種情況，繼續操作

或者

數據結構定義

首先我們需要定義節點元素，每一個節點有左孩子、右孩子、父親節點、節點顏色和存儲的元素，所以我們對節點進行如下定義：

class RedBlackNode<T extends Comparable<T>> {        //黑色節點      public static final int BLACK = 0;      //紅色節點      public static final int RED = 1;      //元素      public T key;      //父節點      RedBlackNode<T> parent;      //左孩子      RedBlackNode<T> left;      //右孩子      RedBlackNode<T> right;        //節點顏色      public int color;        RedBlackNode(){          color = BLACK;          parent = null;          left = null;          right = null;      }        RedBlackNode(T key){          this();          this.key = key;      }  }

接下來是定義紅黑樹，關於左旋和右旋方法就不給出了，紙上畫兩筆就能搞定的事情，我們簡單進行如下定義

public class RedBlackTree<T extends Comparable<T>> {        private RedBlackNode<T> root = null;          private void rotateLeft(RedBlackNode<T> x) {        }        private void rotateRight(RedBlackNode<T> x) {        }  }

插入偽程式碼

當進行插入操作時，我們需要明確插入節點的具體位置，也就是說我們需要查找插入節點的父親節點、左孩子和右孩子且默認插入節點為紅色，最後通過變色或旋轉來進行修復，如下：

 private void insert(RedBlackNode<T> z) {            RedBlackNode<T> y = null;          RedBlackNode<T> x = root;            //若根節點不為空，則循環查找插入節點的父節點          while (!isNull(x)) {              y = x;                // 如果元素值小於當前元素值則從左孩子繼續查找              if (z.key.compareTo(x.key) < 0) {                    x = x.left;              }               // 如果元素值小於當前元素值則從右孩子繼續查找              else {                    x = x.right;              }          }            // 以y作為z的父親節點          z.parent = y;            // 若父親節點為空，說明插入節點為根節點          if (isNull(y))              root = z;          else if (z.key.compareTo(y.key) < 0)              y.left = z;          else              y.right = z;            z.left = null;          z.right = null;          z.color = RedBlackNode.RED;            insertFixup(z);    }

接下來則是實現上述插入修復方法，上述我們分析插入操作幾種的情況的前提是插入節點的父親節點為紅色，所以這裡我們通過循環插入節點的父親節點若為紅色來進行修復，同時呢，無論是插入還是刪除都是有其對稱情況，也就是說我們可將插入和刪除的節點分為是在其父親節點的左側還是右側兩種大的情況，毫無疑問這兩種操作將必定對稱，最淺顯易懂的插入修復方法如下（已加上注釋，可再次藉助於上述分析來看）

private void insertFixup(RedBlackNode<T> z) {            RedBlackNode<T> y = null;            while (z.parent.color == RedBlackNode.RED) {                //如果Z的父親節點在Z祖父節點左側              if (z.parent == z.parent.parent.left) {                    //定義Z的父親兄弟節點                  y = z.parent.parent.right;                    //如果y是紅色                  if (y.color == RedBlackNode.RED) {                        //z的父親變為黑色                      z.parent.color = RedBlackNode.BLACK;                        //y變為黑色                      y.color = RedBlackNode.BLACK;                        //z的祖父變為紅色                      z.parent.parent.color = RedBlackNode.RED;                        //將z的祖父作為z                      z = z.parent.parent;                  }                  // 如果y是黑色且z是右孩子                  else if (z == z.parent.right) {                        // 將z的父親作為z                      z = z.parent;                        //以z的父親節點進行左旋                      rotateLeft(z);                  }                    // 否則如果y黑色且z是左孩子                  else {                        //z的父親變為黑色                      z.parent.color = RedBlackNode.BLACK;                        //z的祖父變為紅色                      z.parent.parent.color = RedBlackNode.RED;                        //以z的祖父右旋                      rotateRight(z.parent.parent);                  }              }                // 如果Z的父親節點在Z祖父節點右側              else {                    // 定義Z的父親兄弟節點                  y = z.parent.parent.left;                    // 如果y是紅色                  if (y.color == RedBlackNode.RED) {                        //z的父親變為黑色                      z.parent.color = RedBlackNode.BLACK;                        //y變為黑色                      y.color = RedBlackNode.BLACK;                        //z的祖父變為紅色                      z.parent.parent.color = RedBlackNode.RED;                        //以z的父親節點進行左旋                      z = z.parent.parent;                  }                    // 如果y是黑色且z是左孩子                  else if (z == z.parent.left) {                        // 將z的父親作為z                      z = z.parent;                        //以z的父親節點進行右旋                      rotateRight(z);                  }                  //否則如果y黑色且z是右孩子                  else {                        //z的父親變為黑色                      z.parent.color = RedBlackNode.BLACK;                        //z的祖父變為紅色                      z.parent.parent.color = RedBlackNode.RED;                        //以z的祖父左旋                      rotateLeft(z.parent.parent);                  }              }          }            // 操作完畢後，根節點重新變為黑色          root.color = RedBlackNode.BLACK;    }

紅黑樹刪除

在上述插入操作中，我們主要是檢查叔叔的顏色從而考慮不同的情況，也就是說插入後違反的主要是兩個連續的紅色。在刪除操作中，我們檢查同級的顏色也就是說檢查兄弟節點的顏色從而考慮不同的情況，刪除主要違反的屬性是子樹中黑色高度的更改，因為刪除黑色節點可能會導致根到葉路徑的黑色高度降低，換言之就是破壞了紅黑樹規則五，那麼我們到底應該如何刪除呢？執行標準的BST刪除，當我們在BST中執行標準刪除操作時，我們最終總是刪除一個葉子節點或只有一個孩子的節點（對於內部節點，我們複製後繼節點，然後遞歸調用刪除後繼節點，後繼節點始終是葉節點或一個有一個孩子的節點），因此，我們只需要處理一個節點為葉子或有一個孩子的情況，因為刪除是一個相當複雜的過程，為了理解刪除，我們引入雙重黑色的概念，當刪除黑色節點並用黑色子節點替換時，該子節點被標記為double black，此時黑色的高度將不變，所以對於刪除我們主要的任務就是將雙黑色轉換為單黑色即可。好像聽起來感覺還是一臉懵逼，莫慌，接下來我依然將用詳細的圖解給大家講解到底雙黑是怎樣的一個神奇存在。刪除操作總的來說分為以下三種情況：

（1）被刪除節點沒有兒子，即為葉節點。（直接刪除）
（2）被刪除節點只有一個兒子。（直接刪除該節點，並用該節點的唯一子節點頂替它的位置）
（3）被刪除節點有兩個兒子。

以上第一和第二種情況就不用我多講，對於第三種情況就涉及到上述我們引入的雙黑的概念，參考鏈接中這樣描述：比如刪除節點v（黑色），則將後繼節點u佔據v節點，由於刪除節點u為黑色，所以導致經過此節點的黑色節點數目減少了一個，為了解決這個問題，我們將佔據的v節點額外引入一個黑色節點，雖然這樣解決了紅黑樹規則五的問題，但是我們知道紅黑樹規則一為每個節點非紅即黑，所以破壞了規則一，然後我們通過變色或旋轉解決。我們將佔據u節點上額外引入一個黑色節點，所以出現雙黑，是不是有點疑惑，這說的到底是什麼意思呢，我們看看如下圖來理解將一目了然，那麼在紅黑樹中如何將如下出現的雙黑變為單黑的呢？請往下看。

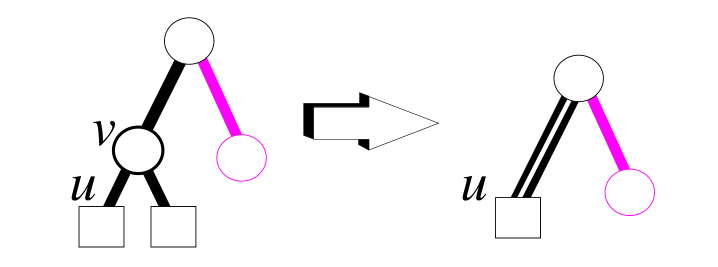
在當前節點Z為雙黑且不是根節點時

【1】左左情況（A節點是其父節點的左節點，C是A的左節點）

（1）將Z兄弟節點即A節點的左孩子變為黑色（2）以Z的父親節點即B節點進行右旋（註：我們將看到右旋時D節點將搭接到B節點上，此時將Z節點上的雙黑給出一個黑色節點來讓D進行搭接，最終雙黑演變成單黑）

【2】右右情況（A節點是其父節點的右節點，C是A的右節點）

（1）將Z兄弟節點即A節點的右孩子變為黑色（2）以Z的父親節點即B節點進行左旋（註：我們將看到左旋時D節點將搭接到B節點上，此時將Z節點上的雙黑給出一個黑色節點來讓D進行搭接，最終雙黑演變成單黑）

【3】左右情況（A節點是其父節點的左節點，C是A的右節點）

（1）將Z兄弟節點即A節點變為紅色（2）將Z兄弟節點即A節點的右孩子變為黑色（3）以Z的兄弟節點A進行左旋（4）演變成如上左左情況，繼續操作

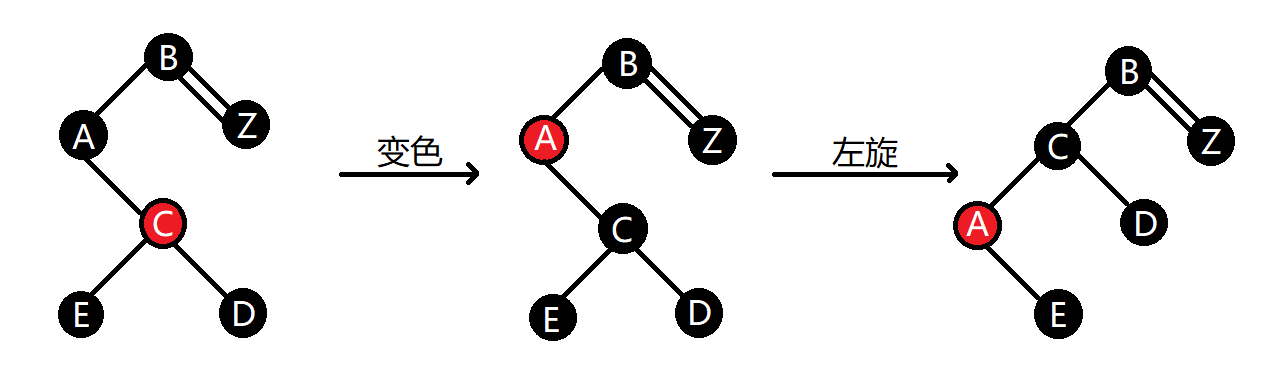
【4】右左情況（A節點是其父節點的右節點，C是A的左節點）

（1）將Z兄弟節點即A節點變為紅色（2）將Z兄弟節點即A節點的左孩子變為黑色（3）以Z的兄弟節點A進行右旋（4）演變成如上右右情況，繼續操作

在當前節點Z兄弟節點為黑色節點且孩子為黑色節點時

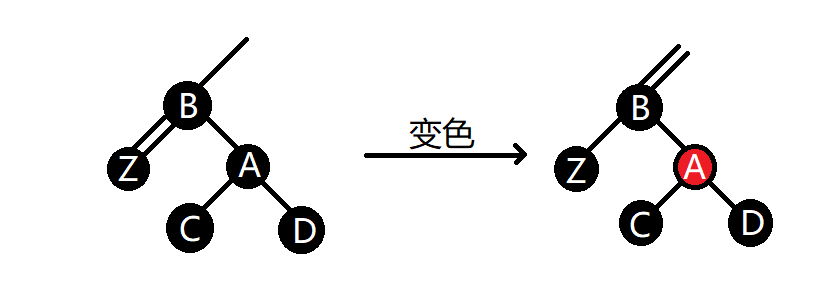
【1】父節點為紅色情況（變色）

（1）將Z節點的父親節點即B節點變為紅色（2）將Z節點的兄弟節點即A節點變為紅色（3）只需變色：紅色+雙黑色=單個黑色

【2】父節點為黑色情況（父節點雙黑，繼續遞歸）

（1）將Z節點的兄弟節點即A節點變為紅色（2）將Z的父親節點即B節點賦給Z節點，繼續進行遞歸操作

在當前節點Z兄弟節點為紅色節點時

【1】Z節點的兄弟節點即A節點在Z節點的父親節點左邊情況

（1）將Z節點的兄弟節點即A節點變為黑色（2）將Z的父親節點即B節點變為黑色（3）以Z節點的父親節點即B節點進行右旋（4）演變成上述父親節點為紅色情況，繼續操作

【2】Z節點的兄弟節點即A節點在Z節點的父親節點右邊情況

（1）將Z節點的兄弟節點即A節點變為黑色（2）將Z的父親節點即B節點變為黑色（3）以Z節點的父親節點即B節點進行左旋（4）演變成上述父親節點為紅色情況，繼續操作

刪除偽程式碼

對於刪除操作，首先我們需要查找到需要刪除的節點，如我們所分析的那樣，若刪除節點孩子只有其一直接刪除即可，若存在兩個孩子，除了找到後繼執行標準的刪除操作外，還需進行刪除修復操作，如下：

 public void remove(RedBlackNode<T> v) {            RedBlackNode<T> z = search(v.key);            RedBlackNode<T> x = null;          RedBlackNode<T> y = null;            //如果z的孩子之一為null，則必須刪除z          if (isNull(z.left) || isNull(z.right))              y = z;                //否則我們需要刪除z的後繼          else y = findSuccessor(z);            // 令x為y的左或右的孩子（y只能有一個子代）          if (!isNull(y.left))              x = y.left;          else              x = y.right;            // 設置y的父親是x的父親          x.parent = y.parent;            // 如果y的父親節點是null，說明x就是根節點          if (isNull(y.parent))              root = x;                //如果y是左孩子，設置x是y的左兄弟          else if (!isNull(y.parent.left) && y.parent.left == y)              y.parent.left = x;                //如果y是右孩子，設置x是y的右兄弟          else if (!isNull(y.parent.right) && y.parent.right == y)              y.parent.right = x;// 如果y是黑色，則違反紅黑樹規則需修復          if (y.color == RedBlackNode.BLACK)              removeFixup(x);  }

private void removeFixup(RedBlackNode<T> x) {            RedBlackNode<T> w;            // 當刪除節點不是根節點且為黑色時          while (x != root && x.color == RedBlackNode.BLACK) {                //如果x在其父親節點左側              if (x == x.parent.left) {                    //定義x的兄弟節點                  w = x.parent.right;                    //w是紅色時                  if (w.color == RedBlackNode.RED) {                        //w變為黑色                      w.color = RedBlackNode.BLACK;                        //x的父親變為紅色                      x.parent.color = RedBlackNode.RED;                        //以x的父親左旋                      rotateLeft(x.parent);                                          w = x.parent.right;                  }                    //w兩個孩子都是黑色時                  if (w.left.color == RedBlackNode.BLACK &&                          w.right.color == RedBlackNode.BLACK) {                        //w變為黑色                          w.color = RedBlackNode.RED;                        //x的父親作為x                      x = x.parent;                  }                  else {                      // w的右孩子為黑色時                      if (w.right.color == RedBlackNode.BLACK) {                            //w的左孩子變為黑色                          w.left.color = RedBlackNode.BLACK;                            //w變為紅色                          w.color = RedBlackNode.RED;                            //以w右旋                          rotateRight(w);                            //重新將x的父親右側孩子賦給w                          w = x.parent.right;                      }                        // w是黑色，右黑子為紅色時                        //w變為x父親的顏色                      w.color = x.parent.color;                        //x的父親變為黑色                      x.parent.color = RedBlackNode.BLACK;                        //w的右孩子變為黑色                      w.right.color = RedBlackNode.BLACK;                        //以x的父親左旋                      rotateLeft(x.parent);                                          
                    x = root;                  }              }             //如果x在其父親節點右側              else {                    //定義x的兄弟節點                  w = x.parent.left;                     //w是紅色時                  if (w.color == RedBlackNode.RED) {                        //w變為黑色                      w.color = RedBlackNode.BLACK;                        //x的父親變為紅色                      x.parent.color = RedBlackNode.RED;                        //以x的父親右旋                      rotateRight(x.parent);                        //重新將x的父親左側孩子賦給w                      w = x.parent.left;                  }                    //w兩個孩子都是黑色時                  if (w.right.color == RedBlackNode.BLACK &&                          w.left.color == RedBlackNode.BLACK) {                        //w變為黑色                                              w.color = RedBlackNode.RED;                        //x的父親作為x                      x = x.parent;                  }                  else {                      // w的右孩子為黑色時                      if (w.left.color == RedBlackNode.BLACK) {                            //w的左孩子變為黑色                          w.right.color = RedBlackNode.BLACK;                            //w變為紅色                          w.color = RedBlackNode.RED;                            //以w左旋                          rotateLeft(w);                            w = x.parent.left;                      }                        // w是黑色，左黑子為紅色時                        //w變為x父親的顏色                      w.color = x.parent.color;                        //x的父親變為黑色                      x.parent.color = RedBlackNode.BLACK;                        //w的左孩子變為黑色                      w.left.color = RedBlackNode.BLACK;                        //以x的父親右旋                      rotateRight(x.parent);                        x = root;                  }              }          }           // 操作完畢後，x節點重新變為黑色          x.color = RedBlackNode.BLACK;  }

總結

本節我們詳細分析了紅黑樹原理，同時給出了大部分偽程式碼，為了讓看文章的童鞋能立馬看的懂，並未做進一步的優化。紙上得來終覺淺，得知此事要躬行，看網上其他人的分析和自己再次進行分析效果可想而知，這篇文章斷斷續續搞了個把月才出來，在這裡我只是通過圖解的方式去理解，看到這篇文章的童鞋再結合網上紅黑樹大量文字的描述估計也能夠理解的七七八八了。有了本節的理解，接下來我們再去分析其他底層實現，必將輕而易舉，文中若有敘述不當或錯誤之處，可在評論中提出。感謝您的閱讀，我們下節再會。