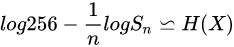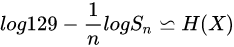對博弈活動中蘊含的資訊理論原理的討論，以及從熵角度看不同詞素抽象方式在WEBSHELL文本檢測中的效果區別

• 2019 年 10 月 3 日
• 筆記

1. 從賽馬說起

0x1：賽馬問題場景介紹

假設在一場賽馬中有m匹馬參賽，令第i匹參賽馬獲勝的概率為p_i，如果第i匹馬獲勝，那麼機會收益為o_i比1，即在第i匹馬上每投資一美元，如果贏了，會得到o_i美元的收益，如果輸了，那麼回報為0。

有兩種流行的馬票：

• a兌1（a-for-1）：開賽前購買的馬票，馬民賽馬前用一美元購買一張機會收益為a美元的馬票，一旦馬票對應的馬在比賽中贏了，那麼他持有的那隻馬票在賽後兌換a美元，否則，他的馬票分文不值。
• b兌1（b-to-1）：賽後交割的馬票，機會收益為b:1，一旦馬票對應的馬輸了，則該馬民賽後必須交納一美元本金，但是如果贏了，賽後可以領取b美元。

當b = a-1時，”a兌1“和”b賒1″兩種馬票的機會收益等價。例如，擲硬幣的公平機會收益倍數是2兌1或者1賒1。

假設某馬民將全部資金分散購買所有參賽的馬匹的馬票，b_i表示其下注在第i匹馬的資金佔總資金的比例，那麼b_i>=0，。如果第i匹馬獲勝，那麼該馬民獲得的回報是下注在i匹馬的資金的o_i倍，而下注在其他馬匹上的資金全部輸掉。於是，賽馬結束時，如果第i匹馬獲勝，那麼該馬民最終所得的資產為原始財富乘以因子b_io_i，而且這樣發生的概率為p_i。

從這裡可以看到，如果馬民採取但是“showhand策略”，即每次都將所有資金全部投資出去，那麼該馬民的整體資產就取決於一個隨機變數b_io_i的速率（稱之為累積因子），不斷累乘利潤。令S_n為該馬民在第n場賽馬結束時的資產，則有：

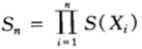，其中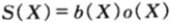是當第X匹馬獲勝時，馬民購買該只馬票所得收益的累積因子。

所以，相對收益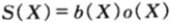是一個累積因子，如果馬民中了X馬票，那麼他的相對收益就是原始財富乘以該因子。

0x2：賽馬投資雙倍率公式定義

由上面對一場賽馬的相對收益公式定義可知，一場賽馬的雙倍率為：

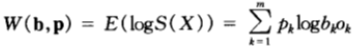
假設賽馬的結果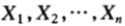為服從p(x)的獨立同分布序列，那麼該馬民在策略b之下的相對收益將以指數因子為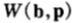呈指數增長，即：

證明過程如下：

由於獨立的隨機變數的函數仍然是獨立的，從而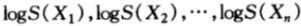也是獨立同分布的，由弱大數定律可得：

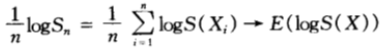
於是有：

由於馬民的相對收益是按照方式增長，因此，接下來的問題是如何在所有投資組合策略b的集合中，尋找使得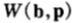最大化的策略，以便得到最快的雙倍率累計結果。

0x3：最大雙倍率策略估計

1. 最優下注策略Kelly策略，以及最優雙倍率的上界

如果選擇b使得雙倍率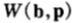達到最大值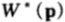，那麼稱該值為最優雙倍率：

上式中，b作為隨機變數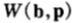，作為b的函數，在約束條件之下求其最大值。可以寫入如下拉格朗日乘子函數並且改變對數的基底（不影響最大化b），則有：

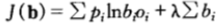
關於b_i求導得到：

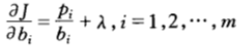
為了求得最大值，令偏導數為0，從而得出：

代入約束條件可得λ=-1，以及b_i=p_i。從而，我們得到b=p為函數J(b)的駐點，即按照比例b=p下注是最優的策略，該策略也被稱為Kelly策略。

由此，我們得到一個最優下註定理，即按比例下注是對數最優的，最優雙倍率的公式計算如下：

，並且當按比例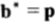的下注策略可以達到該最大值。證明過程如下：

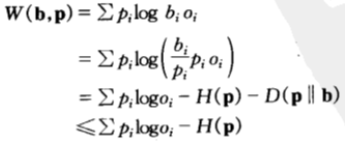
等號成立的充要條件是b=p，即馬民應該按照每匹馬獲勝的概率按比例分散地購買馬票。

考慮僅有兩匹馬參賽的特殊情形，假設馬1獲勝的概率為p₁，馬2獲勝的概率為p₂。假設兩匹馬的機會收益率均等（均為2兌1方式），此時的最優下注策略為按概率比例下注，即b₁=p₁，b₂=p₂。

此時最優雙倍率為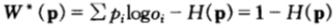，按照這樣的增長率，將導致相對收益無限增長，。

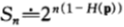至此，我們證明了對於一系列獨立同分布的賽馬，如果馬民將全部現金反覆購買馬票而不是捂住現金不動，那麼按比例下注是相對收益增長最快的策略。

繼續考慮一種特殊情形，即關於某種分布具有公平機會收益倍率的情形。換言之，除了知道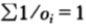之外，無其他資訊可用。此時，記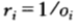，將其視為參賽馬匹的一種概率密度函數（這是用來估計賽馬獲勝概率的所謂馬民法）。在此記號下，雙倍率可以寫為：

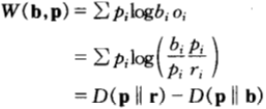
該方程給出了雙倍率在相對熵視角下的另一種解釋：雙倍率是馬民法的估計到真是分布的距離，與馬民下注策略到真是分布的距離之間的差值。

所以，馬民要賺錢，只有當他的估計（由b表示）比馬民法所得的估計（由r表示）更好。上式才為正數，相對收益才會不斷增加。

2. 收益雙倍率守恆定理

考慮一種更特殊的情形是：如果每隻馬票的機會收益倍率為m兌1，此時，機會收益均等，服從均勻分布且最優雙倍率為：

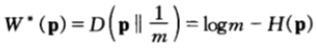
在此情形下可以看到：雙倍率與熵率之和為常數。

這就是雙倍率與熵率對偶守恆定律，即對於均勻的公平機會收益倍率，有：。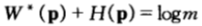

熵每減小一比特，馬民的收益就翻一番，在熵越小的比賽中，馬民的獲利越豐厚。

0x4：賽馬最終收益（相對收益）隨機變數結果討論

在實際的情況中，馬民不一定會傾囊投資，一般來講，應當允許馬民有選擇地保留一部分現金。令b(0)為原始財富中預留為現金的比例，b(1)，b(2)，….，b(m)為分別購買每匹馬的馬票的資金比例。那麼在賽事結束時，最終資產與原始財富的比例（即相對收益）為：

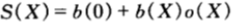
此時的最優化策略依賴於機會收益，我們分情況討論：

1. 服從某種分布的公平機會收益倍率

這種情況下，機會收益分布為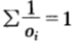，對於公平機會收益倍率，保留現金的選擇並不影響分析。因為我們可以在保留現金的情況下按，i=1，2，…，m比例下注在第i匹馬得到的效果是相同的，因為整個計算是等比例縮放的。於是，馬民到底保存多少現金沒有關係，可以簡單理解為整體馬民投入的錢減少了，多投多賺，少投少賺，依然是按比例下注策略最優。

2. 超公平機會收益倍率

這種情況下，機會收益分布為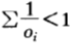，這種比賽的機會收益整體優於公平機會收益倍率的賽事，頗有送錢給馬民的感覺。所以，任何人都希望將全部資金都押進去而不必保留現金。在這種比賽中，依然是按比例下注策略最優。

3. 次公平機會收益倍率

這種情況下，機會收益分布為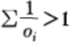，此情形更代表現實生活，這種情況代表了賽馬組織在流程內做了手腳導致收益機會總和小於1。在此種賽馬中，馬民只應該用一部分資金買馬票，而將其他的現金捂住，這是最起碼的策略。此時，按比例下注不再是對數最優了。

Relevant Link: 

《資訊理論基礎》阮吉壽著 - 第六章

2. 邊資訊對賽馬博弈結果的影響

假設馬民具有一些關於賽馬結果的成功和失敗的資訊，例如，馬民或許擁有某些參賽馬匹的歷史記錄，那麼這些資訊會如何影響最終的相對收益呢？

我們將馬民得到的邊資訊定義為互資訊，將因該資訊而導致的雙倍率的增量定義為資訊價值，接下來我們來推導互資訊與雙倍率增量之間的聯繫。

假設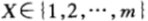為第X只馬票，它獲勝的概率為p(x)，機會收益率為：o(x)兌1。設(X，Y)的聯合概率密度函數為p(x，y)。用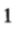，表示已知資訊Y的條件下的下注策略。此處理解為當得知資訊y的條件下，用來買第x只馬票的資金的比例。一般地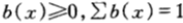，表示無條件下注策略。

設無條件和條件雙倍率分別為：

再設雙倍率增益為：

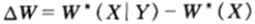
由於獲得某場賽馬X中邊資訊Y而引起的雙倍率的增量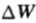滿足：

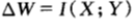
下面來證明該定理。在具有邊資訊的條件下，按照條件比例買馬票，即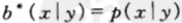，那麼關於邊資訊Y的條件雙倍率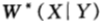可以達到最大值，於是：

，最右一步用到了貝葉斯概率分解公式。

一般地，當無邊資訊時，最優雙倍率為

，這和我們前面討論的一致。

從而，由於邊資訊Y的存在而導致的雙倍率的增量為：

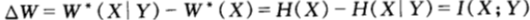
從上面討論可以看到，邊資訊沒有改變雙倍率的期望值，只是改變了對賽馬結果X不確定熵的取值，在守恆定律的作用下，邊資訊給最終雙倍率帶來的增量，等價於邊資訊給賽馬結果X不確定性減低的熵值，即互資訊。

毫無疑問，獨立的邊資訊並不會提高雙倍率，只是降低賽馬結果X的不確定熵。這也一個側面說明了最優雙倍率是一個理論最優值，和具體的過程和結果概率分布X無關。

Relevant Link: 

《資訊理論基礎》阮吉壽著 - 第六章

3. 多輪賽馬序列下的守恆定理

0x1：賽馬序列隨機過程下的相對收益

在賽馬中，邊資訊最通常的表現形式是所有參賽馬匹在過去比賽中的表現（即歷史先驗知識），如果各場賽馬之間是獨立的，那麼這些資訊毫無用途，但是如果假設各場賽馬構成的序列之間存在關聯關係，那麼只要允許使用以前比賽的記錄來決定新一輪賽馬的下注策略，就可以計算出有效的雙倍率。

假設由各場賽馬結果組成的序列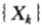是一個隨機過程，假設每場賽馬的下注策略依賴於此前的各次比賽的結果，此時，具有均勻的公平機會收益倍率的比賽的最優雙倍率為；

該最優雙倍率可以在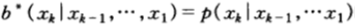時達到。

當第n場賽馬結束時，馬民的相對收益變成：

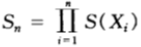
且雙倍率（增長率指數）（假設為m兌1方式）為：

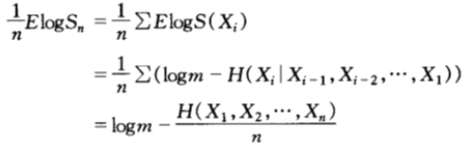
其中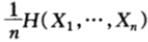，是n場賽馬的平均熵。對於熵率為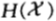的平穩過程，對上式兩邊取極限可得：

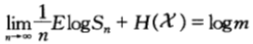
我們再次看到了守恆定理，即熵率與雙倍率之和為常數。

0x2：通過一個隨機過程案例看最優收益增長率公式

筆者思考：賽馬中的最優雙倍率策略，體現了一種絕對理性主義的策略思想，即每一步的決策都完全遵循某種理性主義思辨的結果，不參雜任何主觀的臆斷因素，只要保證了這一點，那麼最終的收益結果就可以達到一個理論最優值，和所參與的博弈遊戲過程都無關，不管過程中勝敗如何，最終得到的收益都是可預期的，且最優的。

我們來看一個撲克牌博弈的例子，叫紅與黑。一副撲克牌分成26張紅和26張黑，每一輪中從兩堆中隨機抽取一張，遊戲參與者需要猜測是紅色還是黑色，直到所有牌發完。我們假設該遊戲的機會收益為2兌1，顯然，紅色和黑色出現的概率相同，這種遊戲是公平機會收益的。

接下來問題來了，你需要採取什麼遊戲策略，以此來博得最大的收益呢？

仔細分析一下就會發現，第一輪時，我們沒有任何先驗知識，紅和黑的概率都是1/2，此後每一輪後，剩下的紅黑牌數量都會發生變化，所以對紅和黑的猜測概率也會不斷發生變化，將整個遊戲看做是一個隨機過程，上一小節已經討論過，最優雙倍率策略為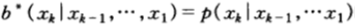，即不斷根據場上當前的概率p(X_i)來決定本輪的猜測策略。

考慮以下兩種下注方案：

• 順序地下注，每一輪中都可以計算出下一張牌的條件概率並且按該條件概率為比率下注。於是，將按照（紅，黑）的概率分布為（1/2，1/2）下注第一張，當第一張為黑色時，再以（26/51，25/51）為概率分布下注第二張，如此下去。
• 一次性下注所有52張牌構成的序列，那麼總共有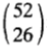種可能的序列，且每個序列出現的概率相等。於是，按比例下注意味著將現金分成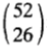份，對每一個序列下注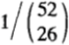的資金。當然假設我們猜對或猜錯每張撲克牌是紅是黑的概率各佔一半。

上述兩種方案本質是等價的。用歸納法來看，52張牌組成的所有序列中，第一張牌是紅色的所有序列恰好佔一半，所以方案2在第一輪賭紅色也是一半資金。以此類推。一般地，如果將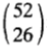種可能的序列視為基本事件，那麼可以驗證：對每個基本事件下注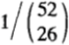資金，則所有下注的策略在任何場合都是與紅色與黑色在此場合出現的概率成比例。類比賭馬模型，我們只將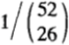資金下注在可能的基本事件上，而且只下注在使得相對收益增長率是2⁵²的因子的觀測序列上，對於其他序列分文不投，那麼，最終相對收益為：

可以看到，此回報並不依賴於具體的序列，這就像AEP中所說的，任何序列都有相同的回報，從這個角度來講，所有序列都是典型的。

Relevant Link: 

《資訊理論基礎》阮吉壽著 - 第六章

4. 熵對語料庫的隨機逼近

為了討論方便，假設英文的字母表由26個字母和空格共計27個字元構成。通過收集一些文本樣本，根據這些文本中的字元的經驗分布建立英文詞頻模型。

0x1：不同Ngram-Size對英文語料的隨機逼近效果分析

在英文語料中，單字母出現的概率遠不是均勻的，例如：

• 字母E出現的概率最高達13%
• 頻率最低的字母Q和Z大約為0.1%

雙字母也一樣遠不是均勻分布，例如：

• 字母Q後面總是跟著字母U
• 但頻率最高的雙字母是TH（通常出現的概率為3.7%），而不是QU

可以利用這些雙字母出現的頻率來估計一個字母后面跟隨另一個字母的概率，即字母表的二階概率轉移矩陣。

同理還可以繼續增加step-size的長度，估計更高階的條件概率並建立更複雜的模型，但是，隨著step-size的增加，很快會遇到”概率空洞問題“。例如，建立三階的馬爾科夫逼近，必須估計條件概率p(x_i | x_i-1，x_i-1，x_i-3)的值，那麼整個三階概率轉移矩陣表就是一個27⁴的巨大表格。這樣，要想得到所有這些3階條件概率的精確估計，就必須引入百萬數量級的樣本。這在實際工程里當然很難做到，不可能總能準備好那麼大量的樣本，所以這部分概率空洞的條件概率項就置零，但是置零又會導致整個句子的累乘式為零，所以為了解決這個問題，又引入平滑技術，相關的細節討論，這裡不再展開，可以參閱另一篇文章。

需要注意的是，不管NLP中引入的什麼平滑技術，還是後來發展處的詞向量嵌入等技術，對於NLP問題來說，我們都可以藉助資訊理論的一個核心概念：”熵“來得到很好的解釋。

N階Ngram詞頻模型是一種隨機逼近的方法（NLP中還有其他隨機逼近方法），使用越高的階，模型的複雜度就越高，相應的對英文語料的逼近就越強。定量地度量所謂的逼近效果的方法就是不確定熵，可以這麼理解：隨著詞模型複雜度的增加，可以捕獲到英文語料中的更多結構資訊，且使得下一個字母的條件不確定性變小，相應的，熵值也就越小。例如：

• 使用0階模型時：熵為log27=4.76比特/字母。
• 使用1階模型時：以列視角看2階概率轉移矩陣，每個字母大多數時候就不是像0階那樣相對均勻分布了，而是集中在某些2階片語中，概率分布的均勻性降低，熵值也就降低了，例如筆者在測試集中算得在1階模型情況下，熵為4.03比特/字母，
• 使用4階模型時：相比於1階，單個字母在不同4階片語中的分配更加集中了，所以熵值進一步降低，例如筆者在測試集中算得在4階模型情況下，熵為2.8比特/字母。

但需要明白的是，即使是4階模型，甚至工程師們最喜歡的5階模型（5-gram）也不能捕獲到英文的所有結構，答案很簡單，因為即使是5階模型，依然存在不小的不確定熵。

0x2：不同馬爾科夫階的模型對Webshell語料庫的隨機逼近效果

為了更形象說明上面的理論，我們藉助香農在最早的論文中提到的一種對英文語料的簡單隨機逼近方法，來一起看一下不同的階數，是如何影響語言模型的隨機逼近效果的。

用一個語料庫（例如一個樣本集合）為道具，若構造二階模型：

• 那麼隨機選擇一個樣本，並隨機選定該樣本內的一個字母，這相當於初始化過程。
• 再隨機地選擇另一個樣本，隨機地從某處開始往下搜索，直到出現第一個字母為止，將緊隨該字母的那個字母選取為第二個字母。如果一直都沒有搜索到第一個字母，則重新選擇另一個樣本。
• 得到第二個字母后，重複前面過程，當我們找到第二個字母后，取其後面的那個字母作為第三個字母。
• 如此下去，我們可以生成一個文本序列，它就是我們的語料庫的二階統計量的擬合。

筆者這裡用網路安全里常見的webshell語料庫為例，下載鏈接在這裡。

# -*- coding: utf-8 -*-    import os  from random import choice      def N_order_Markov_processes(order, path_list):      finnal_sequence = ""        # initial, choice a random file      choice_file_path = choice(path_list)      choice_file_path_content = open(choice_file_path).read()      choice_file_path_word = choice(choice_file_path_content)      finnal_sequence += choice_file_path_word        # search another file      for i in range(order):          while True:              choice_file_path = choice(path_list)              choice_file_path_content_list = list(open(choice_file_path).read())              try:                  last_word_index = choice_file_path_content_list.index(choice_file_path_word) + 1                  choice_file_path_word = choice_file_path_content_list[last_word_index:last_word_index + 1][0]                  finnal_sequence += choice_file_path_word                  break              except Exception, e:                  continue        return finnal_sequence      def main():      path_list = []      ROOT_PATH = '/Users/zhenghan/Downloads/webshell-sample-master/php'      for f in os.listdir(ROOT_PATH):          if f == '.DS_Store':              continue          file_path = os.path.join(ROOT_PATH, f)          path_list.append(file_path)        # generate a 32 length sequence, which each word is an zero-order markov sequence      finnal_sequence = ""      for i in range(32):          finnal_sequence += N_order_Markov_processes(1, path_list)      print "finnal_sequence: ", finnal_sequence      if __name__ == '__main__':      main()

• 0階逼近結果：幾乎沒有捕獲到任何結構資訊
  • 　　
• 1階逼近結果：
  • 　　
• 2階逼近結果：
  • 　　
• 3階逼近結果
  • 　　
• 4階逼近結果
  • 　　
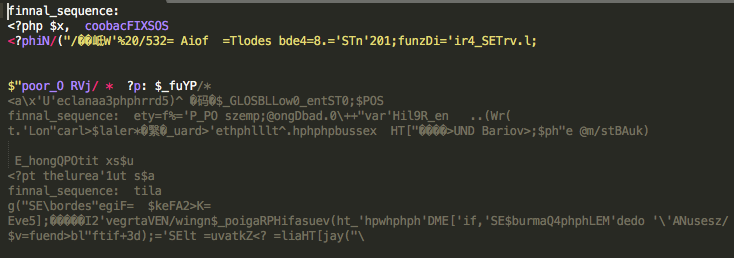
• 5階逼近結果
  • 

可以看到，到5階的時候， 隨機逼近的結果開始出現了正確的php標籤，即開始漸漸捕獲到了語料庫中的一些結構資訊。

Relevant Link:  

https://github.com/ysrc/webshell-sample

5. 從熵角度看不同詞素抽象方式在WEBSHELL文本檢測中的效果區別

0x1：我們要討論什麼問題？

下圖展示了一個webshell文件的截圖

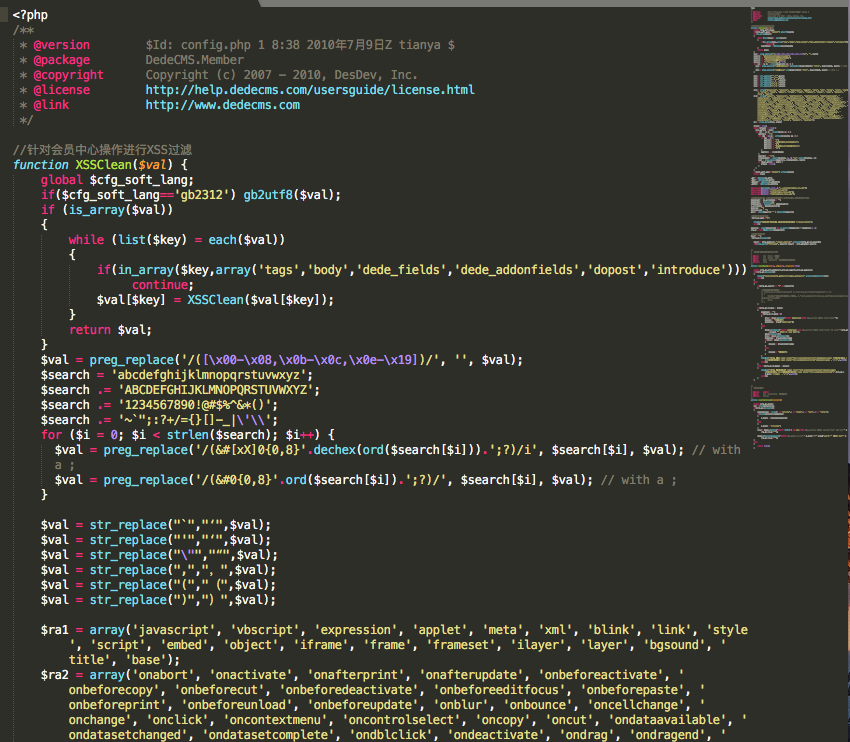
如果要將這類plain text文件輸入機器學習模型，就需要進行向量化特徵工程，但問題是如何進行向量化呢？本章我們來對比兩種主流的方法，並說明其優劣和原理。這兩種方法包括

• char-based vector method：逐個將每個char翻譯為其對應的ascii向量。
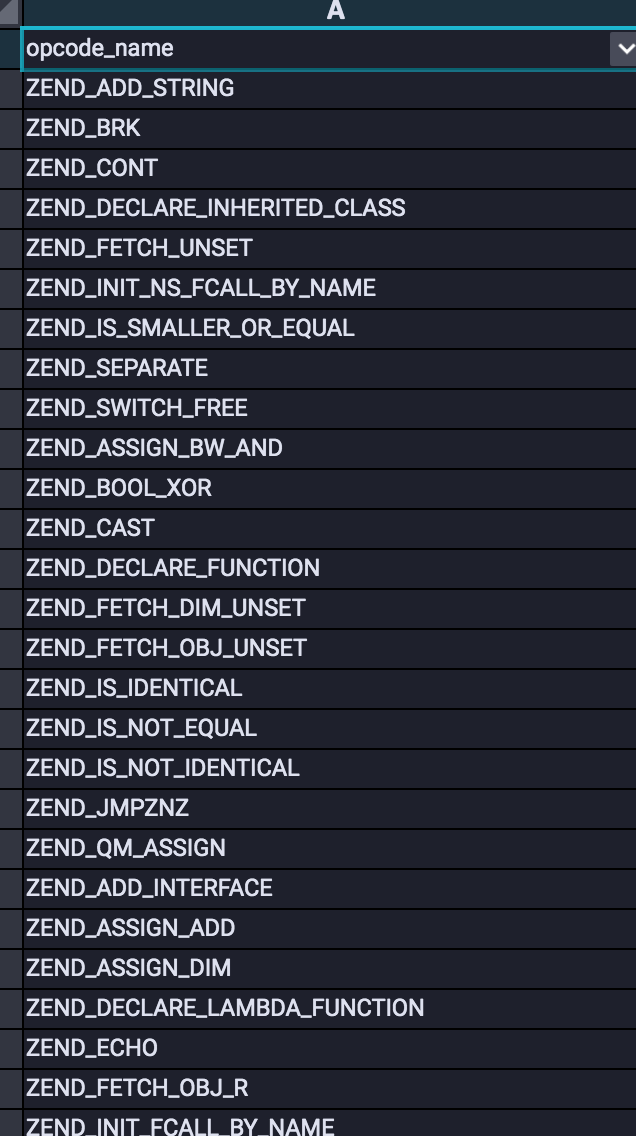
• ast-token-based vector method：將原始文件通過詞法引擎預處理為一種詞法樹的形式，然後按照順序逐個將每個ast-token翻譯為其對應的index索引向量。
  • 　　

上圖給出了ast-token的一個部分截圖，以幫助讀者建立直觀感受。

0x2：如何對一種方案的熵進行建模分析

評估方案本身的熵是一個比較抽象的目標，我們尋找一個等價的問題，我們將每種技術方案都想像成一個人，它們共同在參與一個博弈估計的遊戲。在此遊戲中，給嘉賓任意一個web文件（可能是合法文件也可能是非法webshell文件），隨機指定一個詞素（char或者ast-token）作為初始化，並不斷讓嘉賓猜測下一個出現的詞素。

與賽馬的情形一樣，最優的博弈策略是與下一個詞素出現的條件概率成比例。猜對了詞素的機會收益是：

• char有256個詞素：256兌1
• ast-token有129個詞素：129兌1

由於一連串的分布下注等價於下注一個序列的所有項，因此，在n個詞素之後可得到所有的收益總額為：

• char-based method：S_n = (256)ⁿb(X₁，X₂，…，Xⁿ)
• ast-token-based method：S_n = (129)ⁿb(X₁，X₂，…，Xⁿ)

於是，經過n論下注，相對收益的對數期望滿足下式：

• char-based method： 
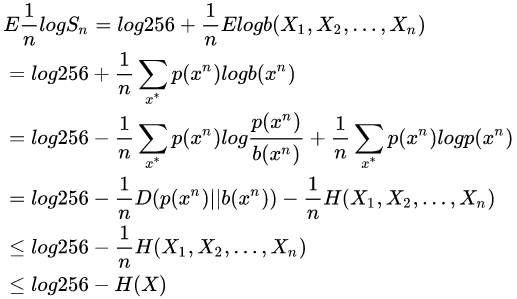
• ast-token-based method：

此處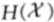是不同方案下，詞素的熵率。於是和是兩種方案各自的熵率的上界。

如果假設webshell文本是遍歷的，且參賽嘉賓使用最優雙倍率策略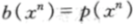（即最大後驗概率估計），那麼其上界估計依概率收斂於各自的熵率，即：

進一步的，又因為熵率的上界為：H(X) <= log^|X|。

所以，綜上所述，ast-token-based的特徵工程方式，要比char-based的方案熵率要小，即不確定度更小，在相同的訓練樣本情況下，ast-token-based方式可以獲得理論上更好的效果。

0x3：評估建模方案好壞的另一個方面 – 互資訊

互資訊的公式如下：

，它定義了X含有Y的資訊量。

這裡X就是不同方案中的特徵向量，而Y就是label標籤位。可以這麼理解，通過輸入特徵向量，能多大程度降低對未知label標籤的模糊程度。

這項評估也很簡單，可以在特徵工程階段進行，在開始實際訓練之前，我們肯定都有一份帶標籤的特徵向量訓練集。通過對X和Y進行相關性分析，可以得到一個互資訊的量化度量。一個好的技術方案，其特徵向量和待預測標籤之間的互資訊應該是很高的。

這裡舉一個虛構的具體例子說明，假設你的訓練集里有如下帶標籤的特徵向量數據。

....  [1，1，1，0，0，0] -> lable = 1  [0，0，0，1，1，1] -> lable = 1  ...  [1，0，0，1，0，1] -> lable = 0  [0，1，1，0，1，0] -> lable = 0  ...

讀者注意到了嗎？上述訓練集中，出現了2對完全相反的特徵向量，但同時其label又是相同的。這個現象怎麼理解呢？用熵的理論視角來看就是：

• 對於label=1來說，該數據集的是一個均勻分布，即最大熵分布，互資訊為0
• 對於label=0來說，該數據集的是一個均勻分布，即最大熵分布，互資訊為0

當然這是一個虛構的極端例子，現實工程中不會極端。但與其類似的場景卻屢見不鮮，筆者自己在項目中也曾經遇到過。當然原因有很多，臟數據總是在所難免的，pure data在實際工程中是很少見的。

筆者這裡想告訴大家的是，在開始訓練之前，一定要關注數據本身的品質，如果訓練集本身對待預測目標的互資訊很低，那麼不管投入多少理論研究資源，都是無法突破理論上界，也不能拿到好的結果。 

0x4：Convolution or Sequence？  

需要注意的是，影像領域的問題因為本身具備幾個核心特性，因而特別適合於CNN卷積網路，例如：

• 平移不變性
• 輕度扭曲近似不變性
• 等比例放縮近似不變性
• 噪點容忍魯棒性
• 邊界漸變性

但是上述的這些特性，當面對的是網路安全中的各類文本的時候，幾乎全都不適用。所以，在實際工程中使用最多的是RNN及其變體的長序列依賴模型，很多文本問題都可以轉化為序列問題來建模和解釋。

Relevant Link: 

https://www.cnblogs.com/LittleHann/p/11266085.html#_lab2_2_0