《神經網路的梯度推導與程式碼驗證》之vanilla RNN的前向傳播和反向梯度推導
- 2020 年 9 月 4 日
- 筆記
- 神經網路的梯度推導與程式碼驗證
在本篇章,我們將專門針對vanilla RNN,也就是所謂的原始RNN這種網路結構進行前向傳播介紹和反向梯度推導。更多相關內容請見《神經網路的梯度推導與程式碼驗證》系列介紹。
注意:
- 本系列的關注點主要在反向梯度推導以及程式碼上的驗證,涉及到的前向傳播相對而言不會做太詳細的介紹。
- 反向梯度求導涉及到矩陣微分和求導的相關知識,請見《神經網路的梯度推導與程式碼驗證》之數學基礎篇:矩陣微分與求導
目錄
提醒:
- 後續會反覆出現$\boldsymbol{\delta}^{l}$這個(類)符號,它的定義為$\boldsymbol{\delta}^{l} = \frac{\partial l}{\partial\boldsymbol{z}^{\boldsymbol{l}}}$,即loss $l$對$\boldsymbol{z}^{\boldsymbol{l}}$的導數
- 其中$\boldsymbol{z}^{\boldsymbol{l}}$表示第$l$層(DNN,CNN,RNN或其他例如max pooling層等)未經過激活函數的輸出。
- $\boldsymbol{a}^{\boldsymbol{l}}$則表示$\boldsymbol{z}^{\boldsymbol{l}}$經過激活函數後的輸出。
這些符號會貫穿整個系列,還請留意。
4.1 vanilla RNN的前向傳播
先貼一張vanilla(樸素)RNN的前傳示意圖。
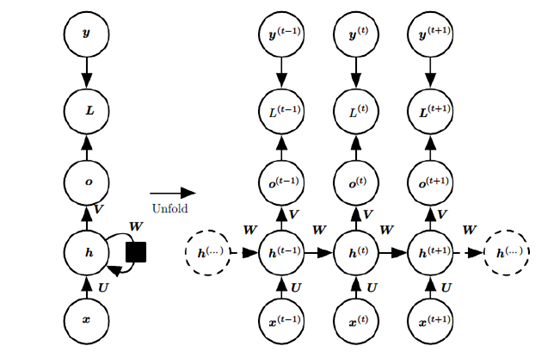
上圖中左邊是RNN模型沒有按時間展開的圖,如果按時間序列展開,則是上圖中的右邊部分。我們重點觀察右邊部分的圖。這幅圖描述了在序列索引號t附近RNN的模型。其中:
- $\boldsymbol{x}^{(t)}$代表在序列索引號$t$時訓練樣本的輸入。注意這裡的$t$只是代表序列索引,不一定非得具備時間上的含義,例如$\boldsymbol{x}^{(t)}$可以是某句子的第$t$個字(的詞向量)。
- $\boldsymbol{h}^{(t)}$代表在序列索引號$t$時模型的隱藏狀態。$\boldsymbol{h}^{(t)}$由$\boldsymbol{x}^{(t)}$和$\boldsymbol{h}^{(t-1)}$共同決定
- $\boldsymbol{a}^{(t)}$代表在序列索引號$t$時模型的輸出。$\boldsymbol{o}^{(t)}$只由模型當前的隱藏狀態$\boldsymbol{h}^{(t-1)}$決定
- $\boldsymbol{L}^{(t)}$代表在序列索引號$t$時模型的損失函數。
- $\boldsymbol{y}^{(t)}$代表在序列索引號$t$時訓練樣本序列的真實輸出
- $\boldsymbol{U},\boldsymbol{W},\boldsymbol{V}$三個矩陣式我們模型的線性相關係數,它們在整個vanilla RNN網路中共享的,這點和DNN很不同。也正因為是共享的,它體現了RNN模型的「循環/遞歸」的核心思想。
4.1.1 RNN前向傳播計算公式
有了上面的模型,RNN的前向傳播演算法就很容易得到了。
對於任意一個序列索引號$t$,我們隱藏狀態$\boldsymbol{h}^{(t)}$由$\boldsymbol{x}^{(t)}$和$\boldsymbol{h}^{(t-1)}$共同得到:
$\boldsymbol{h}^{(t)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t – 1)} + \boldsymbol{b}} \right)$
其中$\sigma$為RNN的激活函數,一般為$tanh$。
序列索引號為$t$時,模型的輸出$\boldsymbol{o}^{(t)}$的表達式也比較簡單:
$\boldsymbol{o}^{(t)} = \boldsymbol{V}\boldsymbol{h}^{(t – 1)} + \boldsymbol{c}$
在最終在序列索引號時我們的預測輸出為:
${\hat{\boldsymbol{y}}}^{(t)} = \sigma\left( \boldsymbol{o}^{(t)} \right)$
對比下列公式:
$\boldsymbol{h}^{(t)} = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t – 1)} + \boldsymbol{b}} \right)$
$\boldsymbol{a}^{l} = \sigma\left( {\boldsymbol{W}^{l}\boldsymbol{a}^{l – 1} + \boldsymbol{b}^{l}} \right)$
上面的是vanilla RNN的$\boldsymbol{h}^{(t)}$的遞推公式,而下面的是DNN中的層間關係的公式。我們可以發現這兩組公式在形式上非常接近。如果將$\boldsymbol{h}^{(t)}$的這種時間上的展開看成類似於DNN這種層間堆疊的話,可以發現vanilla RNN每一「層」除了有來自上一「層」的輸入$\boldsymbol{h}^{(t – 1)}$,還有專屬於這一層的輸入$\boldsymbol{x}^{(t)}$,最重要的是,每一「層」的參數$\boldsymbol{W}$和$\boldsymbol{b}$都是同一組。而DNN則是有專屬於那一層的$\boldsymbol{W}^{l}$和$\boldsymbol{b}^{l}$。
4.2 vanilla RNN的反向梯度推導
RNN反向傳播演算法的思路和DNN是一樣的,即通過梯度下降法一輪輪的迭代,得到合適的RNN模型參數$\boldsymbol{U},\boldsymbol{W},\boldsymbol{V},\boldsymbol{b},\boldsymbol{c}$。由於我們是基於時間反向傳播,所以RNN的反向傳播有時也叫做BPTT(back-propagation through
time)。當然這裡的BPTT和DNN也有很大的不同點,即這裡所有的$\boldsymbol{U},\boldsymbol{W},\boldsymbol{V},\boldsymbol{b},\boldsymbol{c}$在序列的各個位置是共享的,反向傳播時我們更新的是相同的參數。
為了簡化描述,這裡的損失函數我們為交叉熵損失函數,輸出的激活函數為softmax函數,隱藏層的激活函數為tanh函數。
如果RNN在序列的每個位置有輸出,則最終的損失L為所有時間步$t$的loss之和:
$L = {\sum\limits_{t = 1}^{T}L^{(t)}}$
其中,$\boldsymbol{V},\boldsymbol{c}$的梯度計算比較簡單,跟求DNN的BP是一樣的。
根據 數學基礎篇:矩陣微分與求導 1.8節例子的中間結果,我們可以知道:
$\frac{\partial L}{\partial\boldsymbol{c}} = {\sum\limits_{t = 1}^{T}\frac{\partial L^{(t)}}{\partial\boldsymbol{c}}} = {\sum\limits_{t = 1}^{T}{{\hat{\boldsymbol{y}}}^{(t)} – \boldsymbol{y}^{(t)}}}$
$\frac{\partial L}{\partial\boldsymbol{V}} = {\sum\limits_{t = 1}^{T}\frac{\partial L^{(t)}}{\partial\boldsymbol{V}}} = {\sum\limits_{t = 1}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} – \boldsymbol{y}^{(t)}} \right)}\left( \boldsymbol{h}^{(t)} \right)^{T}$
接下來的$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度計算就相對複雜了。從RNN的模型可以看出,在反向傳播時,某一序列位置$t$的梯度由當前位置的輸出對應的梯度和序列索引位置$t+1$時的梯度兩部分共同決定。對於$\boldsymbol{W}$在某一序列位置$t$的梯度損失需要反向傳播一步一步地計算。我們定義序列索引$t$位置的隱藏狀態的梯度為:
$\boldsymbol{\delta}^{(t)} = \frac{\partial L}{\partial\boldsymbol{h}^{(t)}}$
如果我們能知道$\boldsymbol{\delta}^{(t)}$,那麼根據$\boldsymbol{h}^{(t)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t)} + \boldsymbol{W}\boldsymbol{h}^{(t – 1)} + \boldsymbol{b}} \right)$我們就像DNN那樣套用標量對矩陣的鏈式求導法則來進一步得到$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度了。
根據4.1節中的示意圖我們可以輕易發現,當$t = T$,則誤差只有$\left. L^{(T)}\rightarrow\boldsymbol{h}^{(T)} \right.$這麼一條。
所以:
$\boldsymbol{\delta}^{(T)} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(T)} – \boldsymbol{y}^{(T)}} \right)$
而當$t<T$時,$\boldsymbol{h}^{(t)}$的誤差來源有兩條:
1)$\left. L^{(t)}\rightarrow\boldsymbol{h}^{(t)} \right.$
2)$\left. \boldsymbol{h}^{({t + 1})}\rightarrow\boldsymbol{h}^{(t)} \right.$
於是我們得到:
$\boldsymbol{\delta}^{(t)} = \frac{\partial L^{(t)}}{\partial\boldsymbol{h}^{(t)}} + \left( \frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t + 1)}}$
我們來逐項求解:
首先對於$\frac{\partial L^{(t)}}{\partial\boldsymbol{h}^{(t)}}$:
$\boldsymbol{\delta}^{(t)} = \frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = \left( \frac{\partial\boldsymbol{o}^{(t)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{o}^{(t)}} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} – \boldsymbol{y}^{(t)}} \right)$
對於$\left( \frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} \right)^{T}\frac{\partial L^{({t + 1})}}{\partial\boldsymbol{h}^{(t + 1)}}$,我們先關注$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}}$:
因為$\boldsymbol{h}^{(t + 1)} = \sigma\left( \boldsymbol{z}^{(t)} \right) = \sigma\left( {\boldsymbol{U}\boldsymbol{x}^{(t + 1)} + \boldsymbol{W}\boldsymbol{h}^{(t)} + \boldsymbol{b}} \right)$
所以有:
$d\boldsymbol{h}^{(t + 1)} = \sigma^{‘}\left( \boldsymbol{h}^{(t + 1)} \right)\bigodot d\boldsymbol{z}^{(t)} = diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)d\boldsymbol{z}^{(t)} = diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)d\left( {\boldsymbol{W}\boldsymbol{h}^{(t)}} \right) = diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}d\boldsymbol{h}^{(t)}$
所以有:$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}$
於是:
$\boldsymbol{\delta}^{(t)} = \boldsymbol{V}^{T}\left( {{\hat{\boldsymbol{y}}}^{(t)} – \boldsymbol{y}^{(t)}} \right) + \boldsymbol{W}^{T}diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t + 1)}$
有了$\boldsymbol{\delta}^{(T)}$以及從$\boldsymbol{\delta}^{(t + 1)}$到$\boldsymbol{\delta}^{(t)}$的遞推公式,我們可以輕易求出$\boldsymbol{U},\boldsymbol{W},\boldsymbol{b}$的梯度,由於這三組變數在不同的$t$下是公用的,所以由全微分方程可知,這三個變數應當都是在$t$上的某種累加形式。我們定義只在時間步$t$使用的虛擬變數$\boldsymbol{U}^{(t)},\boldsymbol{W}^{(t)},\boldsymbol{b}^{(t)}$,這樣就可以用$\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}$來表示$\boldsymbol{W}$在時間步$t$的時候對梯度的貢獻:
$\frac{\partial L}{\partial\boldsymbol{W}} = {\sum\limits_{t = 1}^{T}\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}} = {\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{W}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}\left( \boldsymbol{h}^{(t – 1)} \right)^{T}}}$
同理,我們得到:
$\frac{\partial L}{\partial\boldsymbol{b}} = {\sum\limits_{t = 1}^{T}{\frac{\partial L}{\partial\boldsymbol{b}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{b}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = {\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}}}}}$
$\frac{\partial L}{\partial\boldsymbol{U}} = {\sum\limits_{t = 1}^{T}{\frac{\partial L}{\partial\boldsymbol{U}^{(t)}} =}}{\sum\limits_{t = 1}^{T}{\left( \frac{\partial\boldsymbol{h}^{(t)}}{\partial\boldsymbol{U}^{(t)}} \right)^{T}\frac{\partial L}{\partial\boldsymbol{h}^{(t)}} = {\sum\limits_{t = 1}^{T}{diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{(t + 1)} \right)} \right)\boldsymbol{\delta}^{(t)}\left( \boldsymbol{x}^{(t)} \right)^{T}}}}}$
4.3 RNN發生梯度消失與梯度爆炸的原因分析
上一節我們得到了從$\boldsymbol{h}^{(t + 1)}$到$\boldsymbol{h}^{(t)}$的遞推公式:
$\frac{\partial\boldsymbol{h}^{(t + 1)}}{\partial\boldsymbol{h}^{(t)}} = diag\left( {\sigma^{‘}\left( \boldsymbol{h}^{({t + 1})} \right)} \right)\boldsymbol{W}$
在求$\boldsymbol{h}^{(t)}$的時候,我們需要從$\boldsymbol{h}^{(T)}$開始根據上面這個公式一步一步推到$\boldsymbol{h}^{(t)}$,可以想像$\boldsymbol{W}$在這期間會被瘋狂地連乘。當我們要求某個時間步$t$下的$\frac{\partial L}{\partial\boldsymbol{W}^{(t)}}$時,這一堆連乘的$\boldsymbol{W}$也會被帶上。結果就是(粗略地分析),如果$\boldsymbol{W}$里的值都比較大,就會發生梯度爆炸,反之則發生梯度消失。
參考資料
- 書籍:《Deep Learning》(深度學習)
(歡迎轉載,轉載請註明出處。歡迎留言或溝通交流: [email protected])


