子字元串查找之————關於KMP演算法你不知道的事
- 2019 年 10 月 28 日
- 筆記
寫在前面:
(閱讀本文前需要了解KMP演算法的基本思路。另外,本著大道至簡的思想,本文的所有例子都會做從頭到尾的講解)
作者翻閱了大量網上現有的KMP演算法部落格,發現廣為流傳的竟然是一種不完整的KMP演算法。即通過next數組來作為有限狀態自動機,以此實現非匹配時的回退。這不失為一種好的方法。
但我們接下來要見識的是一種更好和更完整的方法————擁有完整DFA的KMP演算法
先列出本文要介紹的方法與一般方法對比下的幾大優點:
- 在最壞情況下,對字元串的操作次數僅為一般做法的三分之二。
- 在所有情況下,對字元串的操作數都小於等於一般做法。
- 思路上相對於一般做法更加完整細緻,學習了它一定能讓你對kmp有一個全新的認識。
(讀者可以在通讀全文之後回頭來看這幾句話到底對不對)
一、關於有限狀態自動機(什麼是DFA)
kmp演算法模擬了有限狀態自動機的運行,一般演算法中的next數組和本文中的dfa數組都是作為有限狀態自動機的運行指導。
有限狀態自動機不同,程式運行起來自然會存在不同。
在本文介紹的KMP演算法中,我們使用二維數組DFA來作為有限狀態自動機指導:
- 定義:DFA=new int[R][M],R為文本可能出現的字元種類(EXTENDED_ASCII的R為256位,一般情況下是夠用了),M為模式字元串的長度。
- 空間:DFA佔用空間上比next數組大了R倍,但空間的犧牲必然要迎來性能上的提升!
- 儲存內容:和next數組一樣的是,DFA也儲存了每個位置匹配失敗時模式串的重啟位置,但它更加詳細,DFA針對了匹配失敗時可能出現的不同字元對應了其特定的重啟位置,這樣的好處在後面的性能分析中會降到。
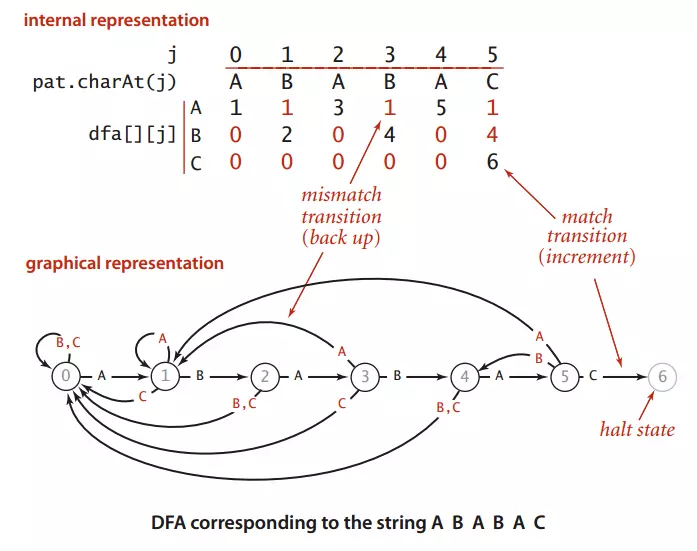
圖1 和模式字元串ABABAC對應的確定有限狀態機自動機
圖一展示了模式字元串pat:ABABAC對應的確定有限狀態機自動機
dfa[A][j]表示:模式串成功匹配到第j個位置時文本這時對應字元為’A’的情況下模式串下一個將要匹配的位置。
拿圖1來說,dfa[A][3]表示匹配到模式串ABABAC的第三位時(B),文本對應的是A,這時模式串將回到dfa[A][3]=1,也就是將模式串回到ABABAC的第一位(B),然後繼續下一位(也是就ABABAC中的第二位,這裡是A)與文本的下一位繼續比較。
似乎蠻複雜的,但理解了它的構造方法之,你就可以靈活使用它。
1、dfa的構造方法:
我們需要藉助j和X來構造dfa,j指向當前的匹配位置,X是匹配失敗時的重啟位置。一開始j和X都設為0。
對於每個j,我們要做的是:
- 將daf[][X]複製到daf[][j](對於匹配失敗的情況)
- 將daf[pat.charAt(j)][j]設為j+1(對於匹配成功的情況)
- 更新X
用程式碼表示如下:
(推薦讀者先大概看看程式碼,再結合下面給出的完整例子,然後做程式碼運行調試)
dfa[pat.charAt(0)][0]=1; for(int X=0,j=1;j<M;j++){//計算dfa[][j] for(int c=0;c<R;c++){//不匹配情況 dfa[c][j]=dfa[c][X]; } dfa[pat.charAt(j)][j]=j+1; X=dfa[pat.charAt(j)][X]; }
在上面程式碼的基礎上來演示一個完整的構造過程:
① j和X都為0,dfa[pat.charAt(0)][0]=1
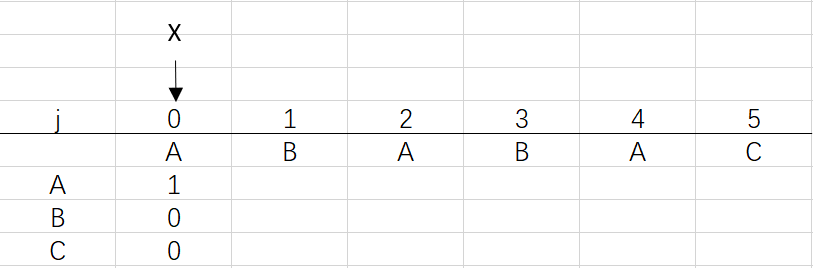
② 進入for循環X=0,j=1:將X的列複製到j的列,再設dfa[pat.charAt(j)][j]=j+1,更新X


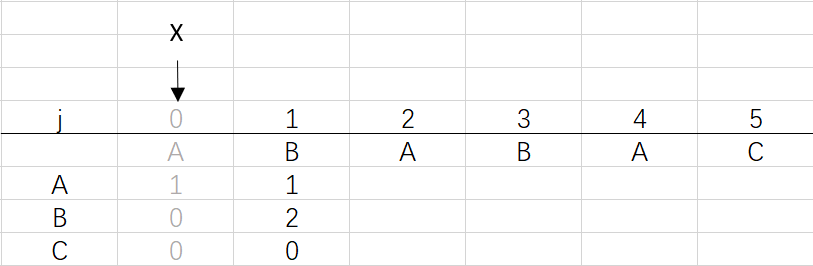
可以看到第三步更新X後X還是0,因為在第二步時X=dfa[pat.charAt(j)][X]=dfa[B][0]=0 (關於X變化的探討接下來就會提到)
③ 第二次循環X=0,j=2:將X的列複製到j的列,再設dfa[pat.charAt(j)][j]=j+1,更新X
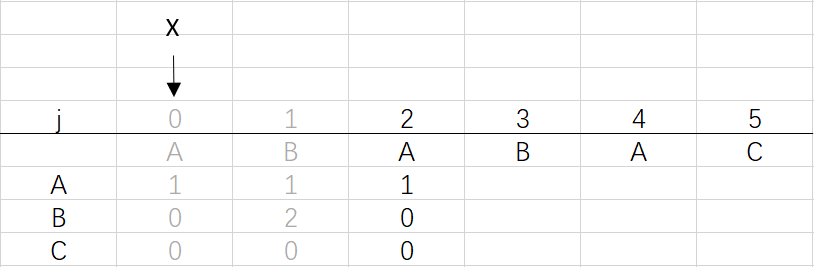
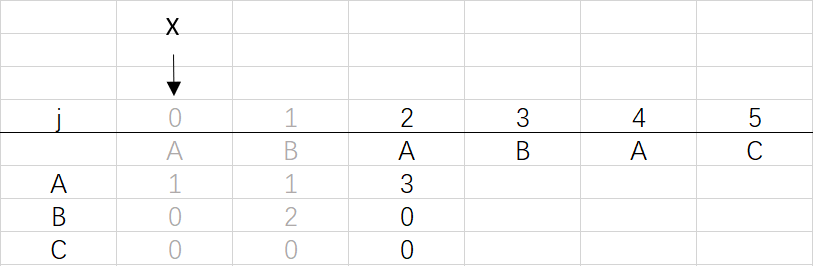
X=dfa[pat.charAt(j)][X]=dfa[A][0]=1
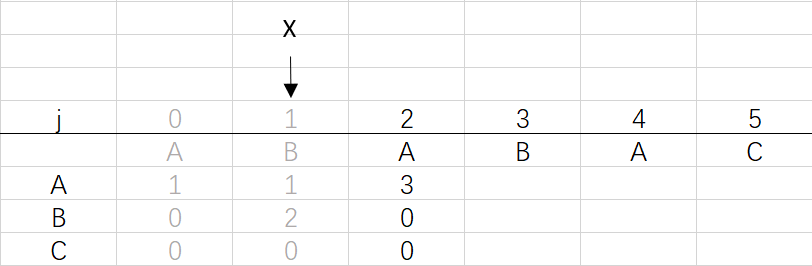
④ 第三次循環X=1,j=3:將X的列複製到j的列,再設dfa[pat.charAt(j)][j]=j+1,更新X
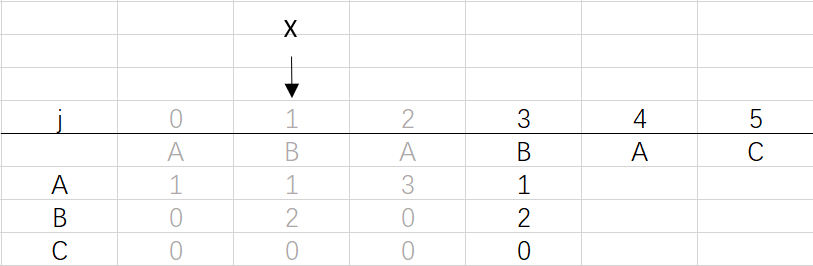
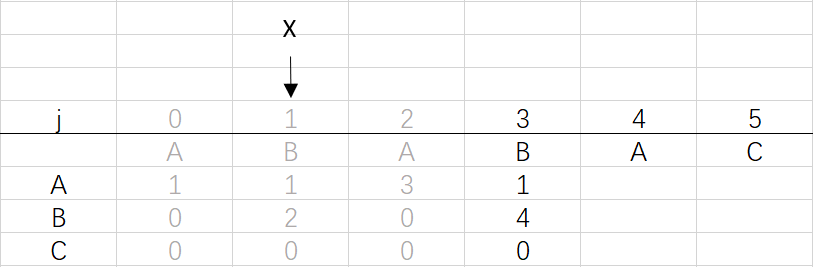
X=dfa[pat.charAt(j)][X]=dfa[B][1]=2

⑤ 第四次循環X=2,j=4:將X的列複製到j的列,再設dfa[pat.charAt(j)][j]=j+1,更新X
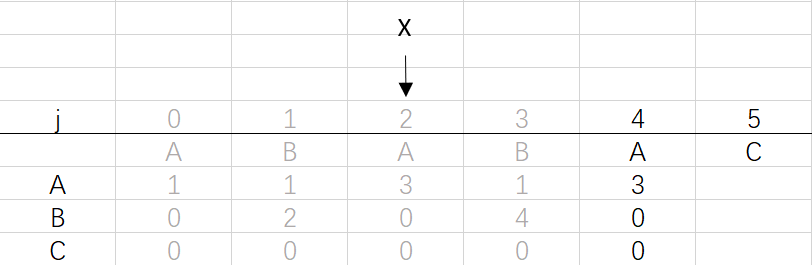
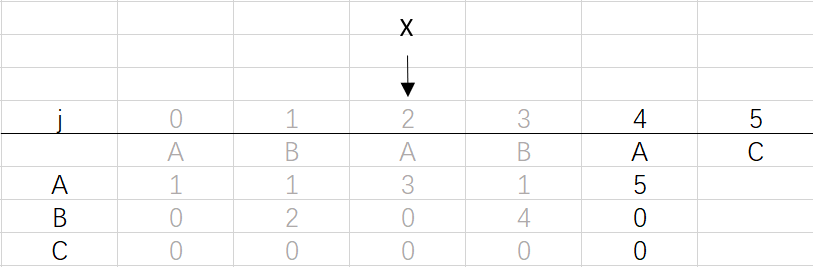
X=dfa[pat.charAt(j)][X]=dfa[A][2]=3
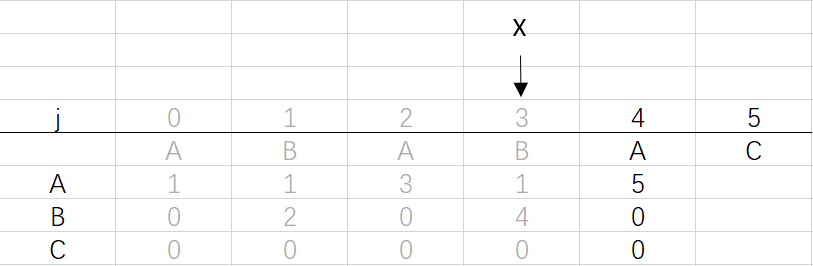
⑥ 第四次循環X=3,j=5:將X的列複製到j的列,再設dfa[pat.charAt(j)][j]=j+1,已經結束到最後一位,不用更新X
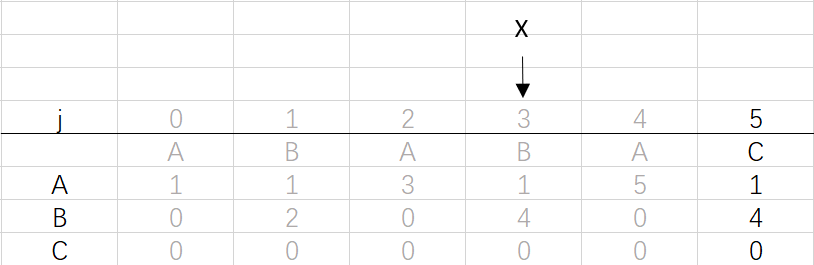
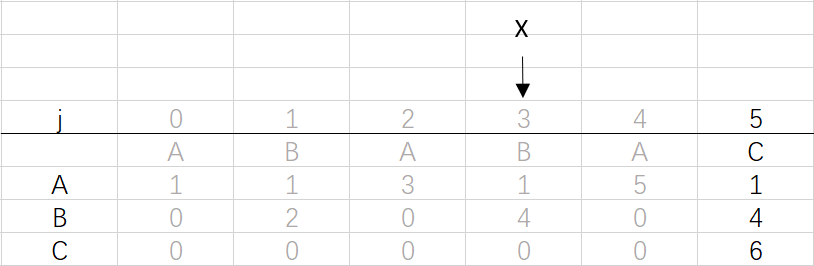
到這裡就結束了模式字元串ABABAC的dfa構造最終得到的結果:
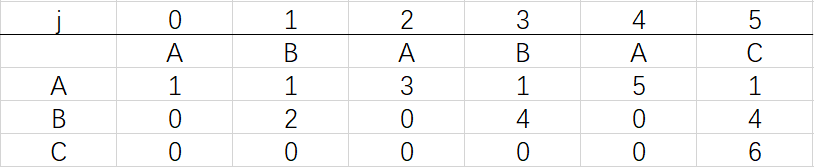
相信大家已經明白了dfa的構造思路
為鞏固練習,下面請讀者自己構造出模式字元串ABRACAD的daf,然後和下圖對照一下是不是一樣
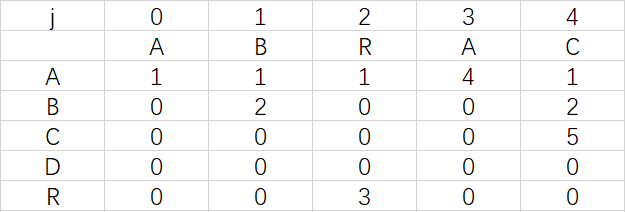
2、關於X的一些問答:
值得一提的是,X是構造dfa的關鍵,下面幾個問答有助於我們理解整個dfa構造。
為什麼每次都能得出X的值?
答:因為X永遠小於j,X走的是j走的老路。
為什麼要把X列複製到j列?
答:dfa里記錄了到每種狀態時可能的所有選擇,如果狀態A發生不匹配時可以回到狀態B繼續匹配,那我們就可以先把狀態B複製到狀態A,這樣在狀態A不匹配時就可以直接使用狀態B的方案。
X的位置何時會發生變化?
X的下一個位置與j當前指向的字元、j之前指向過的字元、X當前位置都有關,事實上不管j當前指向的字元在之前是否出現過,X都可能移動。
X的位置會怎麼變化?
當每次j指向的字元與X指向的字元能夠連續對應上的時候,X就會每次向後移一位(字元與前綴對應時X往後移)。
當j指向的字元在之前沒有出現過,X就會指向0。
3、實例對問題的證明:
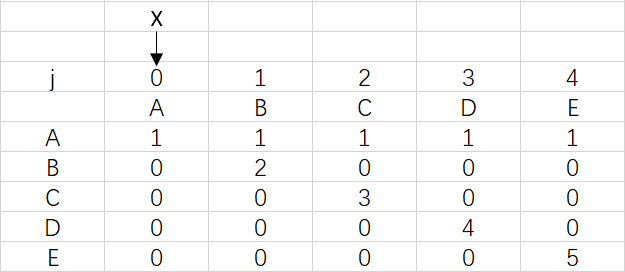
上圖是模式ABCDE的dfa數組,可以觀察到ABCDE中是沒有出現重複字元的,所以到最後X依然指向0
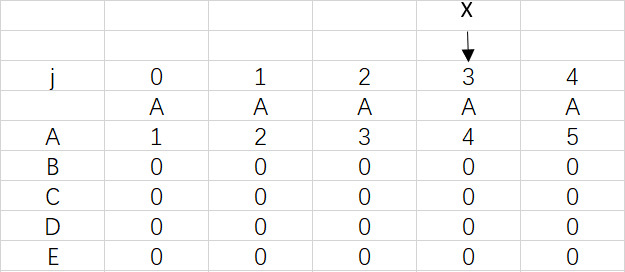
對應極端情況,前面的字元出現重複達到了四次,X也是要移動四次,但只停留在3是因為模式串已經匹配完成,不需要再移動X。
關於X的移動,是需要讀者自己在模擬dfa構造中細想的,想明白了就能全懂KMP,不明白就再看看上面的問題,嘗試自己作答就會有新的心得。
二、改變搜索方法
有了強大的有限狀態自動機,怎麼用它呢?實際使用中是否比原來更強大呢?咱直接將兩者的程式碼貼出來一頓對比,順便說明精妙之處。
大體的思路是一樣的,就是將txt字元串從頭到尾循環一遍,過程中不斷判斷模式串的位置
1、先來看看一般方法中的搜索方法程式碼:
for(i=0;i<n;i++){ while (j>-1&&txt.charAt(i)!=pat.charAt(j)){ j=next[j]; } if(j==-1||txt.charAt(i)==pat.charAt(j)){ j++; } if(j==m){return i-j; } }
一邊從頭到尾循環,一邊判斷j是不是等於m,應該注意到的是,for循環中還包含了一個while,用來做回退和繼續匹配的。
可以發現,這個過程中的操作次數必定是要大於i的(每次for循環都可能要加入while)
2、下面是使用dfa後的搜索方法:
for(j=0,i=0;i<N&&j<M;i++){ j=dfa[txt.charAt(i)][j]; } if(j==M){ System.out.println("匹配成功"); return i-M; }else { System.out.println("匹配失敗"); return N; }
可以看到,在for循環之後,直接進行匹配成功或失敗的判斷,整個過程的操作次數等於i,是小於一般方法的。
三、性能分析對比
①當字元串不匹配時(這是兩種方法差異最大的地方):
使用DFA二維數組作為有限狀態自動機,每次不匹配時都能到達精準位置(對每個不匹配的情況dfa都有記錄在案)。
而使用next一維數組時,在每次匹配失敗後到達的位置是不能確認的,它只是先到達可能的位置。
從可能的最長前綴位置,進行字元的匹配,如果不匹配再移到下一位可能的位置(下標在模式字元串上往前移)。
②當字元串匹配時
在兩種方式中是一樣的,i和j都加一,然後進入下一個for循環。
②最壞情況什麼時候出現
對於一般方法:如果文本為AAAA,模式串為AAAB,這時匹配到最後一位時失敗,j會一步步往前走,這時在搜索方法中操作次數達到了2n,加上構造next數組的n次操作,共3n次操作。
對於完整KMP演算法:上面的情況並不會使它達到3n,因為在j一步步往前走的時候i也會往後走,當i達到n時for循環結束,這樣最多也就操作n次,加上dfa數組的構造需要n次,共2n次操作。
結果:
可以看到,在通常情況下完整KMP演算法的操作次數要比一般演算法的操作次數少
即便是在最壞情況下完整KMP演算法的操作次數也為一般方法的三分之二。
足以證明完整KMP的性能是更優的。
四、完整實現及測試程式碼(java)
1 public class KMP { 2 private String pat; 3 private int dfa[][]; 4 5 public KMP(String pat){//由模式字元串構建dfa 6 this.pat=pat; 7 int M=pat.length(); 8 int R=256; 9 dfa=new int[R][M]; 10 dfa[pat.charAt(0)][0]=1; 11 for(int X=0,j=1;j<M;j++){//計算dfa[][j] 12 for(int c=0;c<R;c++){//不匹配情況 13 dfa[c][j]=dfa[c][X]; 14 } 15 dfa[pat.charAt(j)][j]=j+1; 16 X=dfa[pat.charAt(j)][X]; 17 } 18 } 19 20 public int search(String txt){ 21 int N= txt.length(); 22 int M=pat.length(); 23 int j,i; 24 for(j=0,i=0;i<N&&j<M;i++){ 25 j=dfa[txt.charAt(i)][j]; 26 } 27 if(j==M){ 28 System.out.println("匹配成功"); 29 return i-M; 30 }else { 31 System.out.println("匹配失敗"); 32 return N; 33 } 34 } 35 }
測試例子:
1 @Test 2 public void KMPTest(){ 3 KMP kmp=new KMP("abc"); 4 System.out.println(kmp.search("abfeabcabc")); 5 }