AVL樹旋轉
什麼是AVL樹?
AVL樹是帶有平衡條件的二叉查找樹,一顆AVL樹首先是二叉查收樹(每個節點如果有左子樹或右子樹,那麼左子樹中數據小於該節點數據,右子樹數據大於該節點數據),其次,AVL樹必須滿足平衡條件:每個節點的左子樹和右子樹的高度最多相差1(空樹的高度定義為-1)。
什麼是旋轉?AVL樹為什麼需要用到旋轉?
由於AVL樹本身的性質,當我們插入節點時,有可能會破壞AVL樹的平衡性,使一棵樹的左子樹和右子樹的高度相差大於1,此時就需要對樹進行一些簡單的修正來恢復其性質,這個修正的過程就叫做旋轉。
我們來看一個簡單的例子,比如這棵樹,他在插入節點之後不滿足AVL樹的性質,這時我們可以使用一個旋轉來使他成為一顆AVL樹。
旋轉前: 3
/
2
/
1
這棵樹根節點為3,插入2之後左右子樹高度相差1,再插入1之後左右子樹高度相差2(左子樹高度為1,右子樹高度為-1),此時這棵樹不滿足AVL樹的條件,對這棵樹進行旋轉操作。
旋轉後: 2
/ \
1 3
在經過一次旋轉之後,這棵樹的根節點為2,左右子樹分別為1和3,滿足AVL樹的條件,插入完成。
如何對結點進行旋轉,使其滿足AVL樹的條件?
·單旋轉:
當新插入的節點在二叉樹的外側(左子樹的左側或右子樹的右側),並且此時破壞了AVL樹的平衡,我們使用一個單旋轉來恢復AVL樹的性質。
以左側單旋轉為例,比如剛才那個例子中,旋轉前根節點為3,左子樹高度為1,右子樹高度為-1。此時我們先讓左子樹2的右子樹(在這裡為NULL)變為根節點的新左子樹
3
2 / \
/ NULL NULL
1
再讓原來的根節點3變為節點2的右子樹
2
/ \
1 3
此時可以算是完成了一次單旋轉,2變為新的根節點。這個旋轉後的樹滿足AVL樹的條件。
左側單旋轉程式碼:
1 typedef struct TreeNode 2 { 3 ElementType Element; 4 struct TreeNode *Left; 5 struct TreeNode *Right; 6 int Height; 7 }*AvlTree; 8 int NodeHeight(AvlTree P) 9 { 10 if(P == NULL) return -1; 11 else return P->Height; 12 } 13 AvlTree SingleRotateWithLeft(AvlTree T) 14 { 15 /* T指向原來的根節點,T1指向旋轉後的根節點 */ 16 AvlTree T1; 17 T1 = T->Left; 18 19 /* 根節點的左子樹等於其原來左子樹的右子樹 */ 20 T->Left = T1->Right; 21 22 /* 讓原來的根節點成為新的根節點的右子樹 */ 23 T1->Right = T; 24 25 /* 重新設置節點高度 */ 26 T->Height = Max(NodeHeight(T->Left),NodeHeight(T->Right))+1; 27 T1->Height = Max(NodeHeight(T1->Left),T->Height)+1; 28 29 /* 將新的根節點返回 */ 30 return T1; 31 }
右側單旋轉和左側差不多:
1 1
\ / \
2 2 3
\
3
1 AvlTree SingleRotateWithRight(AvlTree T) 2 { 3 AvlTree T1; 4 T1 = T->Right; 5 T->Right = T1->Left; 6 T1->Left = T; 7 T->Height = Max(NodeHeight(T->left),NodeHeight(T->Right))+1; 8 T1->Height = Max(T->Height,NodeHeight(T1->Right))+1; 9 return T1; 10 }
·雙旋轉
當新插入的節點在二叉樹的內側(左子樹的右側或右子樹的左側),並且此時破壞了AVL樹的平衡,我們使用一個單旋轉來恢復AVL樹的性質。
這裡還是先以左側雙旋轉為例,我們來嘗試建立一棵樹並初始化,並設根節點為3
3
/ \
NULL NULL
我們插入一個1,由於這個樹應滿足二叉查找樹的條件,所以1應該插入根節點3的左側
3
/ \
1 NULL
再插入一個2,由二叉查找樹條件,2應該插在1的右側
3
/ \
1 NULL
\
2
此時,由於根節點左子樹和右子樹高度相差大於一,所以此時不滿足AVL樹的條件,此時需要一個雙旋轉來使這棵樹成為AVL樹
首先,我們對根節點的左子樹1進行右側單旋轉:
(根據單旋轉的方法,令 1 的右子樹等於原來右子樹 2 的左子樹 NULL ,再讓 1 成為 2 的左子樹,原來指向 1 的指針指向 2)
3
/
2
/
1
然後,再對根節點3進行左側單旋轉:
(根據單旋轉的方法,令 3 的左子樹等於原來左子樹 2 的右子樹 NULL ,再讓 3 成為 2 的右子樹,2成為根節點)
2
/ \
1 3
此時,完成了一個雙旋轉,這棵樹滿足AVL樹的條件。
看程式碼:
1 AvlTree DoubleRotateWithLeft(AvlTree T) 2 { 3 // 在根節點的左子樹進行右側單旋轉 4 T->Left = SingleRotateWithRight(T->Left); 5 6 // 在根節點處進行左側單旋轉 7 return SingleRotateWithLeft(T); 8 }
在右側進行雙旋轉和左側類似:
1
\
3
/
2
對根節點的右子樹進行左側單旋轉:
1
\
2
\
3
對根節點進行右側單旋轉:
2
/ \
1 3
1 AvlTree DoubleRotateWithRight(AvlTree T) 2 { 3 // 在T的右子樹進行左側單旋轉 4 T->Right = SingleRotateWithLeft(T->Right); 5 6 // 在根節點T處進行右側單旋轉 7 return SingleRotateWithRight(T); 8 }
至此,我們已經看到了AVL樹的四種旋轉(左右單旋轉,左右雙旋轉),有了這些旋轉的方法,我們就可以在插入節點時進行判斷,判斷當前插入節點之後的樹是否需要進行旋轉,以及需要哪種旋轉,進而實現任意在AVL樹中插入節點。
具體的插入節點程式碼實現不在這裡放出,可以參考《數據結構與演算法分析-C語言描述版》(本文中的觀點與程式碼大都來自此書,稍有改動,加入自己的理解)。
看一下程式碼實現後的運行結果:
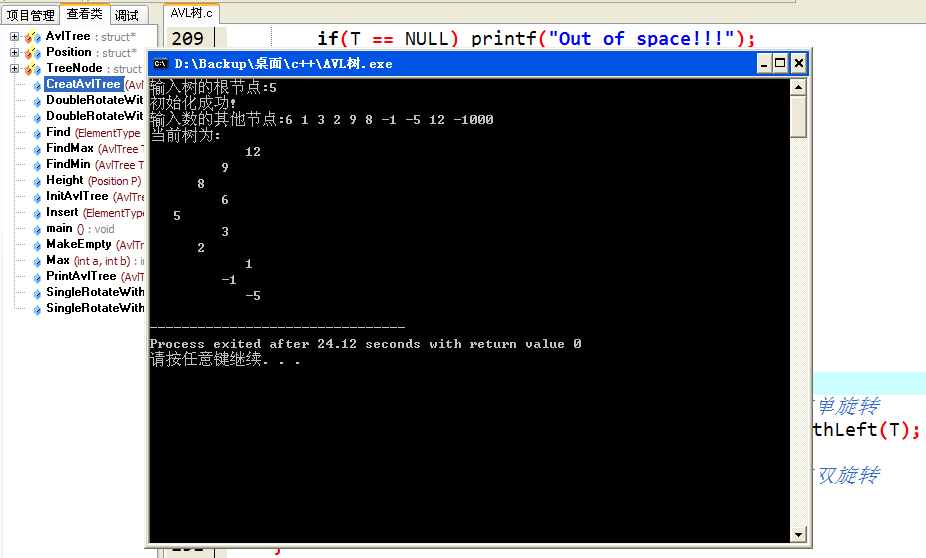
註: 這裡輸入的最後一個參數 -1000 是輸入的結束條件,輸出的樹是逆時針旋轉90°之後的樹。


