【異常檢測】孤立森林(Isolation Forest)演算法簡介
簡介
工作的過程中經常會遇到這樣一個問題,在構建模型訓練數據時,我們很難保證訓練數據的純凈度,數據中往往會參雜很多被錯誤標記雜訊數據,而數據的品質決定了最終模型性能的好壞。如果進行人工二次標記,成本會很高,我們希望能使用一種無監督演算法幫我們做這件事,異常檢測演算法可以在一定程度上解決這個問題。
異常檢測分為 離群點檢測(outlier detection) 以及 奇異值檢測(novelty detection) 兩種.
- 離群點檢測:適用於訓練數據中包含異常值的情況,例如上述所提及的情況。離群點檢測模型會嘗試擬合訓練數據最集中的區域,而忽略異常數據。
- 奇異值檢測:適用於訓練數據不受異常值的污染,目標是去檢測新樣本是否是異常值。 在這種情況下,異常值也被稱為奇異點。
孤立森林 (Isolation Forest, iForest)是一個基於Ensemble的快速離群點檢測方法,具有線性時間複雜度和高精準度,是符合大數據處理要求的State-of-the-art演算法。由南京大學周志華教授等人於2008年首次提出,之後又於2012年提出了改進版本。適用於連續數據(Continuous numerical data)的異常檢測,與其他異常檢測演算法通過距離、密度等量化指標來刻畫樣本間的疏離程度不同,孤立森林演算法通過對樣本點的孤立來檢測異常值。具體來說,該演算法利用一種名為孤立樹iTree的二叉搜索樹結構來孤立樣本。由於異常值的數量較少且與大部分樣本的疏離性,因此,異常值會被更早的孤立出來,也即異常值會距離iTree的根節點更近,而正常值則會距離根節點有更遠的距離。此外,相較於LOF,K-means等傳統演算法,孤立森林演算法對高緯數據有較好的魯棒性。其可以用於網路安全中的攻擊檢測,金融交易欺詐檢測,疾病偵測,和雜訊數據過濾等。
舉個例子:
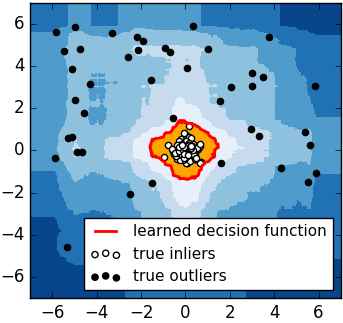
對於如何查找哪些點是否容易被孤立,iForest使用了一套非常高效的策略。假設我們用一個隨機超平面來切割數據空間, 切一次可以生成兩個子空間(想像拿刀切蛋糕一分為二)。之後我們再繼續用一個隨機超平面來切割每個子空間,循環下去,直到每子空間裡面只有一個數據點為止。直觀上來講,我們可以發現那些密度很高的簇是可以被切很多次才會停止切割,但是那些密度很低的點很容易很早的就停到一個子空間了。上圖裡面黑色的點就很容易被切幾次就停到一個子空間,而白色點聚集的地方可以切很多次才停止。
演算法
怎麼來切這個數據空間是iForest的設計核心思想,本文僅介紹最基本的方法。由於切割是隨機的,所以需要用Ensemble的方法來得到一個收斂值(蒙特卡洛方法),即反覆從頭開始切,然後平均每次切的結果。iForest 由 T 個 iTree 組成,每個 iTree 是一個二叉樹結構。該演算法大致可以分為兩個階段,第一個階段我們需要訓練出 T 顆孤立樹,組成孤立森林。隨後我們將每個樣本點帶入森林中的每棵孤立樹,計算平均高度,之後再計算每個樣本點的異常值分數。
第一階段,步驟如下:
- 從訓練數據中隨機選擇
Ψ個點樣本點作為樣本子集,放入樹的根節點。 - 隨機指定一個維度(特徵),在當前節點數據中隨機產生一個切割點
p(切割點產生於當前節點數據中指定維度的最大值和最小值之間)。 - 以此切割點生成了一個超平面,然後將當前節點數據空間劃分為2個子空間:把指定維度里小於
p的數據放在當前節點的左子節點,把大於等於p的數據放在當前節點的右子節點。 - 在子節點中遞歸步驟(2)和(3),不斷構造新的子節點,直到子節點中只有一個數據(無法再繼續切割)或子節點已到達限定高度。
- 循環(1)至(4),直至生成
T個孤立樹iTree。
第二階段:
獲得T個iTree之後,iForest訓練就結束,然後我們可以用生成的iForest來評估測試數據了。對於每一個數據點 \(x_i\),令其遍歷每一顆孤立樹iTree,計算點 \(x_i\) 在森林中的平均高度 \(h(x_i)\) ,對所有點的平均高度做歸一化處理。異常值分數的計算公式如下所示:
S\left ( x,\psi \right )= 2^{-\frac{E\left ( h\left ( x \right ) \right )}{c\left ( \psi \right )}}
\]
其中
c\left ( \psi \right ) = \left\{\begin{matrix} 2H\left ( \psi – 1 \right ) – 2 \left ( \psi – 1 \right )/\psi, \psi > 2\\ 1, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \psi = 2\\ 0, \quad \quad \quad \quad \quad \quad \quad \quad otherwise \end{matrix}\right.
\]
\(H(i)\) 是調和數,可以通過 ln(i) + 0.5772156649(歐拉常數)來估算。分值越小表示數據越為異常。
示例:
>>> from sklearn.ensemble import IsolationForest
>>> X = [[-1.1], [0.3], [0.5], [100]]
>>> clf = IsolationForest(random_state=0).fit(X)
>>> clf.predict([[0.1], [0], [90]])
array([ 1, 1, -1])
補充:
-
iForest具有線性時間複雜度。因為是Ensemble的方法,所以可以用在含有海量數據的數據集上面。通常樹的數量越多,演算法越穩定。由於每棵樹都是互相獨立生成的,因此可以部署在大規模分散式系統上來加速運算。
-
iForest不適用於特別高維的數據。由於每次切數據空間都是隨機選取一個維度,建完樹後仍然有大量的維度資訊沒有被使用,導致演算法可靠性降低。高維空間還可能存在大量噪音維度或無關維度(irrelevant attributes),影響樹的構建。對這類數據,建議使用子空間異常檢測(Subspace Anomaly Detection)技術。此外,切割平面默認是axis-parallel的,也可以隨機生成各種角度的切割平面,詳見「On Detecting Clustered Anomalies Using SCiForest」。
-
iForest僅對Global Anomaly敏感,即全局稀疏點敏感,不擅長處理局部的相對稀疏點(Local Anomaly)。目前已有改進方法發表於PAKDD,詳見「Improving iForest with Relative Mass」。
-
iForest推動了重心估計(Mass Estimation)理論發展,目前在分類聚類和異常檢測中都取得顯著效果,發表於各大頂級數據挖掘會議和期刊(如SIGKDD,ICDM,ECML)。
參考文章:
iForest (Isolation Forest)孤立森林 異常檢測 入門篇
Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. “Isolation forest.”Data Mining, 2008. ICDM’08. Eighth IEEE International Conference on. IEEE, 2008.
Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. “Isolation-based anomaly detection.”*ACM Transactions on Knowledge Discovery from Data (TKDD)*6.1 (2012): 3.

