查找–斐波那契查找
- 2019 年 10 月 26 日
- 筆記
1、什麼是斐波那契數列?
1、1、2、3、5、8、13、21、……
斐波那契數列又被成為黃金分割數列,因為 前一項/後一項越來越趨近於0.618
由上面的數列,可以發現 除了前兩項,後面每一項都是前兩項的和,如3+5=8、8+13=21…..
由此可以得到一下等式
F(n)=F(n-1)+F(n-2) (除了前兩項)
2、斐波那契查找和斐波那契數列有什麼聯繫?
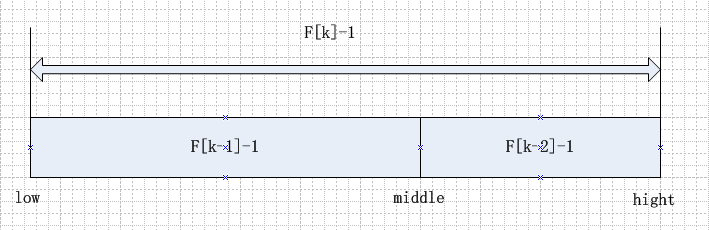
斐波那契查找原理與前兩種相似,僅僅改變了中間結點(mid)的位置,mid不再是中間或插值得到,而是位於黃金分割點附近,即mid=low+F(k-1)-1(F代表斐波那契數列)
關於F(k)-1
由斐波那契數列可知,F(k)=F(k-1)+F(k-2),那F(k)-1=(F(k-1)-1)+(F(k-2)-1)+1,所以數組長度只要滿足 F(k)-1,就可以將數組分為F(k-1)-1和F(k-2)-1左右兩部分,其中mid=low+F(k-1)-1
3、程式碼實現
目標;查找99 int[] a={0,16,24,35,47,59,62,73,88,99};
public static int MaxSize=20; //先為斐波那契數列設置長度 //構建你波拉契數列 public static int[] fib(){ int[] f=new int[MaxSize]; f[0]=1; f[1]=1; for (int i=2;i<MaxSize;i++){ f[i]=f[i-1]+f[i-2]; } return f; }
public static int fibSearch(int[] arr,int key){ int left=0; //初始指向最數組最左邊 int right=arr.length-1; //初始指向最數組最右邊 int k=0; //指示斐波那契數列的下標,初始為0是為了根據數組長度確定數組需要擴展的長度 int mid=0; int[] f=fib(); //獲取斐波那契數列 while (arr.length>f[k]-1){ //這裡的f[k]是arr距離斐波那契數列最近的數值,為什麼-1,為了符合數組特性(數組最大元素下標是數組長度-1) k++; } int[] temp=Arrays.copyOf(arr,f[k]); //為什麼構建一個新數組,因為下面需要對數組進行擴展,查找最後還要用到原始數組,所以不能用原始數組 //擴展數組 for (int i=right+1;i<temp.length;i++){ //這裡為什麼用temp.length?因為上面Arrays.copyOf(arr,f[k])已經對數組擴展了,這裡我們進行的是把擴展的值都改為原始數組的最大值 temp[i]=arr[right]; } while (left<=right){ mid=left+f[k-1]-1; //這裡就是為mid確定位置,位置確定請看上面的圖 if (key<temp[mid]){ //如果當前mid值大於key,說明key在mid左邊部分,繼續對左邊的F[k-1]-1部分進行分割 right=mid-1; k--; }else if (key>temp[mid]){ left=mid+1; k-=2; }else { if (mid<arr.length){ //查找值的下標在arr數組額範圍內,直接返回 return mid; }else { //不在就返回right,為什麼?因為後面幾位的值和right的值是一樣的,說明查找的值就是right return right; } } } //都找不到返回-1 return -1; }
public static void main(String[] args) { int[] a={0,16,24,35,47,59,62,73,88,99}; int key=99; System.out.println(fibSearch(a,key)); }
4、斐波那契查找缺陷
- 只適用於順序表
- 有序數組