深度學習筆記——常用的激活（激勵）函數

　　激活函數（又叫激勵函數，後面就全部統稱為激活函數）是模型整個結構中的非線性扭曲力，神經網路的每層都會有一個激活函數。那他到底是什麼，有什麼作用？都有哪些常見的激活函數呢？

　　深度學習的基本原理就是基於人工神經網路，訊號從一個神經元進入，經過非線性的 activation function，傳入到下一層神經元；再經過該層神經元的 activate，繼續往下傳遞，如此循環往複，直到輸出層。正是由於這些非線性函數的反覆疊加，才使得神經網路有足夠的 capacity來抓取複雜的pattern，在各個領域取得 state-of-the-art 的結果。顯而易見，activate function 在深度學習舉足輕重，也是很活躍的研究領域之一。所以下面學習一下深度學習中常用的激勵函數。

1，什麼是激活函數？

　　神經網路中的每個神經元節點接受上一層神經元的輸出值作為本神經元的輸入值，並將輸入值傳遞給下一層，輸入層神經元節點會將輸入屬性直接傳遞到下一層（隱層或輸出層）。在多層神經網路中，上層節點的輸出和下層節點的輸入之間具有一個函數關係，這個函數稱為激活函數。

2，為什麼要用激活函數（激活函數的用途）？

　　簡單來說：1，加入非線性因素 2，充分組合特徵

　　在神經網路中，如果不對上一層結點的輸出做非線性轉換的話（其實相當於激活函數為 f(x)=x），再深的網路也是線性模型，只能把輸入線性組合再輸出，不能學習到複雜的映射關係，而這種情況就是最原始的感知機（perceptron），那麼網路的逼近能力就相當有限，因此需要使用激活函數這個非線性函數做轉換，這樣深層神經網路表達能力就更加強大了（不再是輸入的線性組合，而是幾乎可以逼近任意函數）。

　　我們知道深度學習的理論基礎是神經網路，在單層神經網路中（感知機 Perceptron），輸入和輸出計算關係如下：

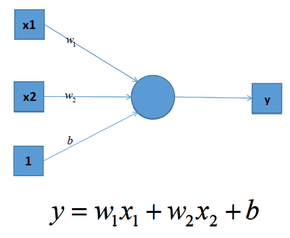
　　可見，輸入與輸出是一個線性關係，對於增加了多個神經元之後，計算公式也是類似，如下圖：

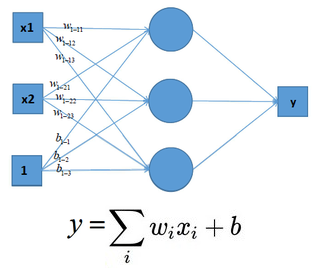
　　這樣的模型就只能處理一些簡單的線性數據，而對於非線性數據則很難有效的處理（也可通過組合多個不同線性表示，但這樣更加複雜和不靈活），如下圖所示：

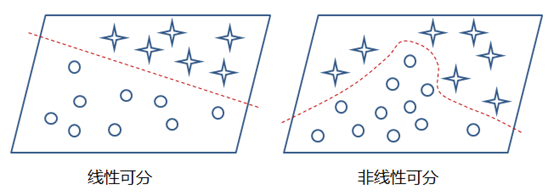
　　那麼，通過在神經網路中加入非線性激勵函數後，神經網路就有可能學習到平滑的曲線來實現對非線性數據的處理了，如下圖所示：

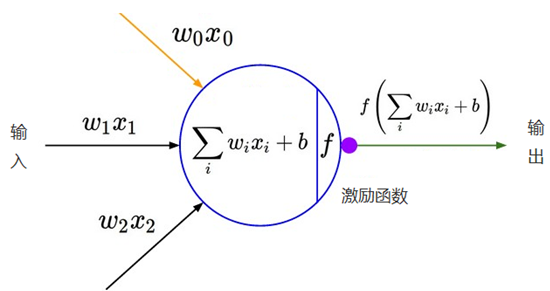
　　因此，神經網路中激勵函數的作用通俗上講就是將多個線性輸入轉換為非線性的關係。如果不使用激勵函數的話，神經網路的每層都只是做線性變換，即使是多層輸入疊加後也還是線性變換。通過激勵函數引入非線性因素後，使神經網路的表達能力更強了。

3，有哪些激活函數，都有什麼性質和特點？

　　早期研究神經網路主要採用Sigmoid函數或者 tanh函數，輸入有界，很容易充當下一層的輸入。近些年ReLU函數及其改進型（如Leaky-ReLU，P-ReLU，R-ReLU等）在多層神經網路中應用比較多。下面學習幾個常用的激勵函數。

3.1 激活函數的性質

非線性

　　當激活函數是線性的時候，一個層的神經網路就可以逼近基本上所有的函數了。但是，如果激活函數是恆定激活函數的時候（即 f(x)=x），就不滿足這個性質了，而且如果MLP使用的是恆等激活函數，那麼其實整個網路根單層神經網路是等價的。

可微性

　　當優化方法是基於梯度的時候，這個性質是必須的。

單調性

　　當激活函數是單調的時候，單層網路能夠保證是凸函數

f(x) $f (x) \approx x$ x

　　當激活函數滿足這個性質的時候，如果參數的初始化是 random的很小的值，那麼神經網路的訓練將會很高效；如果不滿足這個性質，那麼就需要很用心的去設置初始值

輸出值的範圍

　　當激活函數的輸出值是有限的時候，基於梯度的優化方法會更加穩定，因為特徵的表示受有限權值的影響更顯著；當激活函數的輸出是無限的時候，模型的訓練會更加高效，不過在這種情況下，一般需要更小的 learning rate。

　　基於上面性質，也正是我們使用激活函數的原因

3.2 Sigmoid 函數

　　Sigmoid函數時使用範圍最廣的一類激活函數，具有指數函數的形狀，它在物理意義上最為接近生物神經元。其自身的缺陷，最明顯的就是飽和性。從函數圖可以看到，其兩側導數逐漸趨近於0，殺死梯度。

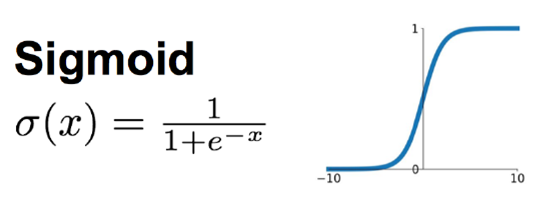
　　Sigmoid激活函數和導函數如下：

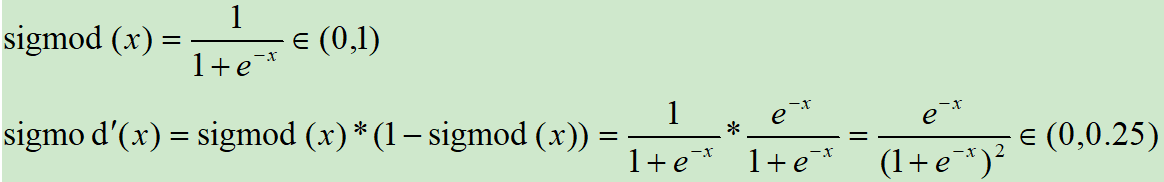
　　對應的影像如下：

　　畫圖對應的程式碼如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,1/(1+np.exp(-x)))
plt.title("y = 1/(1+exp(-x))")
plt.show()

plt.plot(x,np.exp(-x)/(1+np.exp(-x))**2)
plt.title("y = exp(-x)/(1+exp(-x))^2")
plt.show()

優點：

　　這應該是神經網路中使用最頻繁的激勵函數了，它把一個實數（輸入的連續實值）壓縮到0到1之間，當輸入的數字非常大的時候，結果會接近1，當輸入非常大的負數時，則會得到接近0的結果。在早期的神經網路中使用地非常多，因為它很好地解釋了神經元受到刺激後是否被激活和向後傳遞的場景（0：幾乎沒有被激活；1：完全被激活）。

缺點：

　　不過近幾年在深度學習的應用中比較少見到它的身影，因為使用Sigmoid函數容易出現梯度彌散或者梯度飽和。當神經網路的層數很多時，如果每一層的激活函數都採用Sigmoid函數的話，就會產生梯度彌散和梯度爆炸的問題，其中梯度爆炸發生的概率非常小，而梯度消失發生的概率比較大。

　　上面也畫出了Sigmoid函數的導數圖，我們可以看到，如果我們初始化神經網路的權重為[0, 1] 之間的隨機數值，由反向傳播演算法的數學推導可知，梯度從後向前傳播時，每傳遞一層梯度值都會減少為原來的 0.25 倍，因為利用反向傳播更新參數時，會乘以它的導數，所以會一直減少。如果輸入的是比較大或比較小的數（例如輸入100，經Sigmoid 函數後結果接近於1，梯度接近於0），會產生梯度消失線性（飽和效應），導致神經元類似於死亡狀態。而當網路權值初始化為（1 , +∞）區間的值，則會出現梯度爆炸情況。

　　還有Sigmoid函數的output不是0均值（zero-centered），這是不可取的，因為這會導致後一層的神經元將得到上一層輸出的非 0 均值的訊號作為輸入。產生一個結果就是：如 x > 0 ，則 f = w^Tx + b，那麼對 w 求局部梯度則都為正，這樣在反向傳播的過程中 w 要麼都往正方向更新，要麼都往負方形更新，導致一種捆綁的效果，使得收斂緩慢。當然了，如果按照 batch 去訓練，那麼那個 batch 可能得到不同的訊號，所以這個問題還是可以緩解一下的。因此，非0均值這個問題雖然會產生一些不好的影響，不過跟上面提到的梯度消失問題相比還是好很多的。

　　最後就是對其解析式中含有冪函數，電腦求解時相對比較耗時，對於規模比較大的深度網路，這會較大的增加訓練時間。

科普：什麼是飽和呢？

　　當一個激活函數 h(x) 滿足：

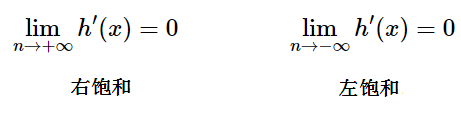
　　當 h(x) 即滿足左飽和又滿足又飽和，稱之為飽和。

3.3 tanh函數

　　tanh是雙曲函數中的一個，tanh() 為雙曲正切。在數學中，雙曲正切 tanh 是由雙曲正弦和雙曲餘弦這兩者基本雙曲函數推導而來。

　　正切函數時非常常見的激活函數，與Sigmoid函數相比，它的輸出均值是0，使得其收斂速度要比Sigmoid快，減少迭代次數。相對於Sigmoid的好處是它的輸出的均值為0，克服了第二點缺點。但是當飽和的時候還是會殺死梯度。

　　tanh激活函數和導函數分別如下：

　　對應的影像分別為：

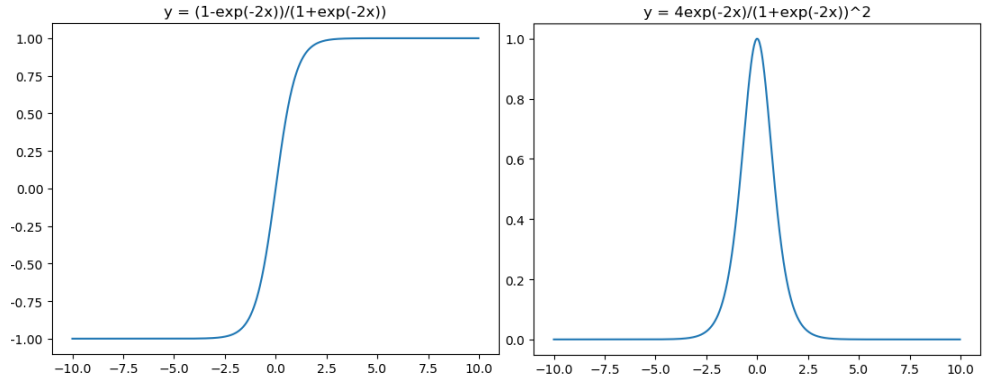
　　影像所對應的程式碼如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,(1-np.exp(-2*x))/(1+np.exp(-2*x)))
plt.title("y = (1-exp(-2x))/(1+exp(-2x))")
plt.show()

plt.plot(x,4*np.exp(-2*x)/(1+np.exp(-2*x))**2)
plt.title("y = 4exp(-2x)/(1+exp(-2x))^2")
plt.show()

　　在神經網路的應用中，tanh通常要優於Sigmoid的，因為 tanh的輸出在 -1~1之間，均值為0，更方便下一層網路的學習。但是有一個例外，如果做二分類，輸出層可以使用 Sigmoid，因為它可以算出屬於某一類的概率。

　　tanh 讀作 Hyperbolic Tangent，它解決了Sigmoid函數的不是 zero-centered 輸出問題，tanh 函數將輸入值壓縮到 -1 和 1 之間，該函數與 Sigmoid 類似，也存在著梯度彌散或梯度飽和和冪運算的缺點。

為什麼tanh 相比 Sigmoid收斂更快

　　1，梯度消失問題程度：

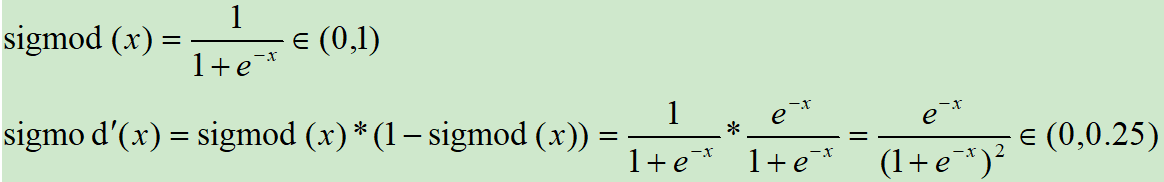
　　可以看出，tanh(x) 的梯度消失問題比 sigmoid要輕，梯度如果過早消失，收斂速度較慢。

　　2，以零為中心的影響，如果當前參數（w0, w1）的最佳優化方向是（+d0, -d1），則根據反向傳播計算公式，我們希望x0和x1符號相反，但是如果上一級神經元採用 Sigmoid 函數作為激活函數，Sigmoid不以零為中心，輸出值恆為正，那麼我們無法進行更快的參數更新，而是走Z字形逼近最優解。

3.4，ReLU 函數

　　針對Sigmoid函數和tanh的缺點，提出ReLU函數。

　　線性整流函數（Rectified Linear Unit, ReLU），又稱修正線性單元，是一種人工神經網路中常用的激活函數（activation function），通常指代以斜坡函數及其變種為代表的非線性函數。

　　最近幾年比較受歡迎的一個激活函數，無飽和區，收斂快，計算簡單，有時候會比較脆弱，如果變數的更新太快，還沒有找到最佳值，就進入小於零的分段就會使得梯度變為零，無法更新直接死掉了。

　　ReLU激活函數和導函數分別為

　　對應的影像分別為：

　　影像對應的程式碼如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,np.clip(x,0,10e30))
plt.title("y = relu(x)=max(x,0)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,x>0,"o")
plt.title("y = relu'(x)")
plt.show()

ReLU優點：

　　ReLU是修正線性單元（The Rectified Linear Unit）的簡稱，近些年來在深度學習中使用得很多，可以解決梯度彌散問題，ReLU函數就是一個取最大值函數，因為它的導數等於1或者就是0（注意：它並不是全區間可導的，但是我們可以取 Sub-gradient）。相對於sigmoid和tanh激勵函數，對ReLU求梯度非常簡單，計算也很簡單，可以非常大程度地提升隨機梯度下降的收斂速度。（因為ReLU是線性的，而sigmoid和tanh是非線性的）。所以它有以下幾大優點：

1，解決了gradient vanishing （梯度消失）問題（在正區間）
2，計算方便，求導方便，計算速度非常快，只需要判斷輸入是否大於0
3，收斂速度遠遠大於 Sigmoid函數和 tanh函數，可以加速網路訓練

ReLU缺點：
　　但ReLU的缺點是比較脆弱，隨著訓練的進行，可能會出現神經元死亡的情況，例如有一個很大的梯度流經ReLU單元後，那權重的更新結果可能是，在此之後任何的數據點都沒有辦法再激活它了。如果發生這種情況，那麼流經神經元的梯度從這一點開始將永遠是0。也就是說，ReLU神經元在訓練中不可逆地死亡了。所以它的缺點如下：

1，由於負數部分恆為零，會導致一些神經元無法激活
2，輸出不是以0為中心

　　ReLU的一個缺點是當x為負時導數等於零，但是在實踐中沒有問題，也可以使用leaky ReLU。總的來說，ReLU是神經網路中非常常用的激活函數。

　　ReLU 也有幾個需要特別注意的問題：

　　1，ReLU 的輸出不是 zero-centered

　　2，Dead ReLU Problem，指的是某些神經元可能永遠不會被激活，導致相應的參數永遠不會被更新，有兩個主要原因可能導致這種情況產生：

　　（1）非常不幸的參數初始化，這種情況比較少見

　　（2） learning rate 太高，導致在訓練過程中參數更新太大，不幸使網路進入這種狀態。

　　解決方法是可以採用 Xavier 初始化方法，以及避免將 learning rate 設置太大或使用 adagrad 等自動調節 learning rate 的演算法。儘管存在這兩個問題，ReLU目前仍然是最常見的 activation function，在搭建人工神經網路的時候推薦優先嘗試。

ReLU 激活函數在零點是否可導？

　　答案是在零點不可導。

　　這裡首先需要複習一些數學概念：連續與可導。

　　連續：設函數 y = f(x) 在點 x0 的某一領域內有定義，如果函數 y = f(x) 當 x——> x0 時的極限存在，且，則稱函數 y = f(x) 在點 x0 處連續。

　　這裡需要注意左極限等於右極限等於函數值，即，顯然 ReLU函數是連續的在零點。但是不可導。

　　可導：設函數 y = f(x) 在點 x0 的某一鄰域內有定義，則當自變數 x 在 x0 處取得增量 Δx 時，相應的 y 取增量；如果 Δx ——> 0 時， Δy / Δx 極限存在，則稱 y= f(x) 在點 x0 處可導，並稱這個極限為函數 y = f(x) 在點 x0 處的導數，記為：

　　然而左導數和右導數並不相等，因而函數在該處不可導，實際上，如果函數導數存在，當且僅當其左右導數均相等。

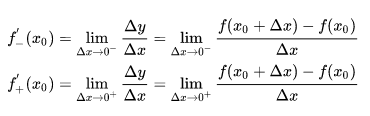
　　而 ReLU 左導數等於 0 ，右導數等於1，因此不可導。

ReLU 在零點不可導，那麼在反向傳播中如何處理？

　　caffe源碼~/caffe/src/caffe/layers/relu_layer.cpp倒數第十行程式碼：

bottom_diff[i] = top_diff[i] * ((bottom_data[i] > 0)+ negative_slope * (bottom_data[i] <= 0));

　　這句話就是說間斷點的求導按左導數來計算。也就是默認情況下（negative_slope=0）,RELU的間斷點處的導數認為是0。

3.5 Leaky ReLU 函數（P-ReLU）

　　Leaky ReLU激活函數和導函數如下：

　　對應的影像分別如下：

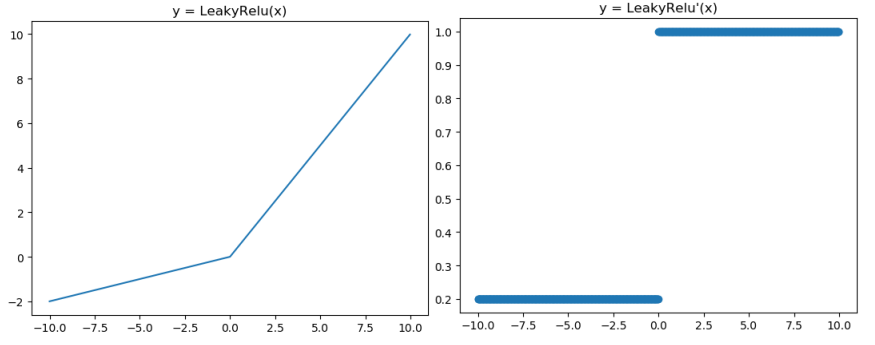
　　影像對應的程式碼如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
a = 0.2
plt.plot(x,x*np.clip((x>=0),a,1))
plt.title("y = LeakyRelu(x)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,np.clip((x>=0),a,1),"o")
plt.title("y = LeakyRelu'(x)")
plt.show()

　　人們為了解決 Dead ReLU Problem，提出了將 ReLU 的前半段設為 ax 而非0，通常 a = 0.01，另外一種直觀的想法是基於參數的方法，即 ParmetricReLU ： f(x)=max(ax, x)，其中 a 可由方向傳播演算法學出來。理論上來說，Leaky ReLU 有ReLU的所有優點，外加不會有 Dead ReLU 問題，但是在實際操作當中，並沒有完全證明 Leaky ReLU 總是好於 ReLU。

　　Leaky ReLU 主要是為了避免梯度小時，當神經元處於非激活狀態時，允許一個非0的梯度存在，這樣不會出現梯度消失，收斂速度快。他的優缺點根ReLU類似。

3.6 ELU 函數（Exponential Linear Unit）

　　融合了Sigmoid和ReLU，左側具有軟飽和性，右側無飽和性。

　　右側線性部分使得ELU訥訥狗狗緩解梯度消失，而左側軟飽能夠讓 ELU 對輸入變化或雜訊更魯棒。因為函數指數項所以計算難度會增加。

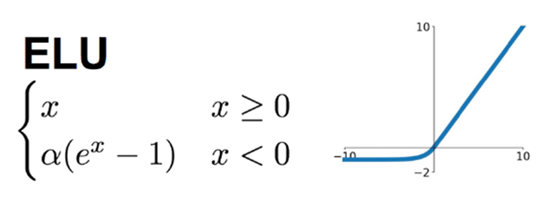
　　ELU在正值區間的值為x本身，這樣減輕了梯度彌散問題（x>0區間導數處處為1），這點跟ReLU、Leaky ReLU相似。而在負值區間，ELU在輸入取較小值時具有軟飽和的特性，提升了對雜訊的魯棒性。

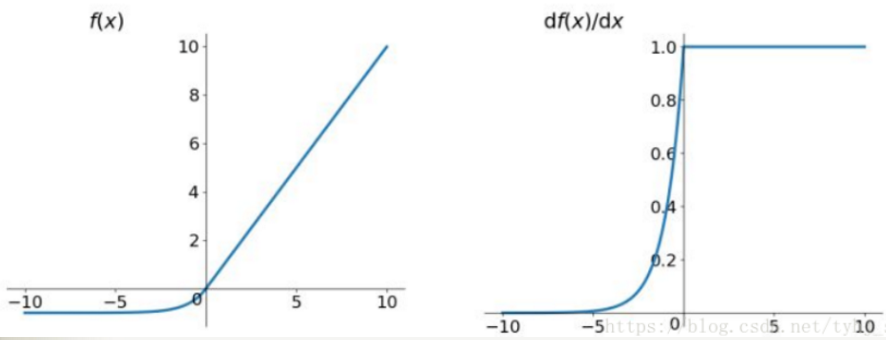
　　函數及導數的影像如下圖所示：

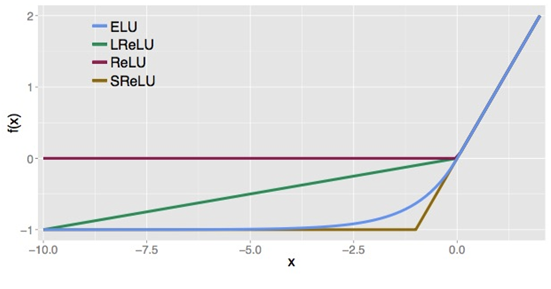
　　下圖是ReLU、LReLU、ELU的曲線比較圖：

　　ELU 也是為了解決 ReLU 存在的問題而提出，顯然，ELU有 ReLU的基本所有優點，以及不會出現Dead ReLU 問題，輸出的均值接近0，zero-centered，它的一個小問題在於計算量稍大。類似於 Leaky ReLU ，理論上雖然好於 ReLU，但是實際使用中目前並沒有好的證據 ELU 總是優於 ReLU。

3.7 Maxout 函數

　　這個函數可以參考論文《maxout networks》，Maxout 是深度學習網路中的一層網路，就像池化層，卷積層一樣，我們可以把 maxout 看成是網路的激活函數層，我們假設網路某一層的輸入特徵向量為： X=(x1, x2, ….xd)，也就是我們輸入的 d 個神經元，則maxout隱藏層中神經元的計算公式如下：

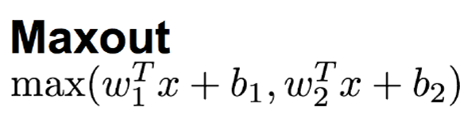
　　Maxout也是近些年非常流行的激勵函數，簡單來說，它是ReLU和Leaky ReLU的一個泛化版本，當w1、b1設置為0時，便轉換為ReLU公式。

　　它用於RELU的優點而且沒有死區，但是它的參數數量卻增加了一倍。

　　因此，Maxout繼承了ReLU的優點，同時又沒有「一不小心就掛了」的擔憂。但相比ReLU，因為有2次線性映射運算，因此計算量也會翻倍。

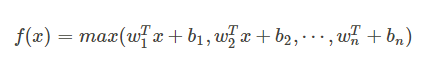
　　權重 w 是一個大小為（d, m , k）三維矩陣， b 是一個大小為（m, k）的二維矩陣，這兩個就是我們需要學習的參數。如果我們設定參數為 k=1，那麼這個時候，網路就類似於以前我們所學習的普通的 MLP網路。

　　我們可以這樣理解，本來傳統的 MLP 演算法在第 i 層到第 i+1 層，參數只有一組，然而現在我們不這麼幹了，我們在這一層同時訓練 n 組的 w, b 參數，然後選擇激活值 Z 最大的作為下一層神經元的激活值，這個 max(Z) 函數即充當了激活函數。

3.8 ReLU6 函數

　　ReLU 在 x > 0 的區域使用 x 進行線性激活，有可能造成激活後的值太大，影響模型的穩定性，為抵消 ReLU激活函數的線性增長部分，可以使用ReLU6函數。

　　ReLU6 激活函數和導函數分別如下：

　　對應的影像分別為：

　　函數對應的程式碼如下：

from matplotlib import pyplot as plt
import numpy as np
fig = plt.figure()
x = np.arange(-10, 10, 0.025)
plt.plot(x,np.clip(x,0,6))
plt.title("y = relu6(x)=min(max(x,0),6)")
plt.show()

from matplotlib import pyplot as plt
plt.plot(x,(x>0)&(x<6),"o")
plt.title("y = relu6'(x)")
plt.show()

3.9 Softmax 函數

　　提起softmax函數，我們首先理清全連接層到損失層之間的計算，來看下面這幅圖（侵刪！）：

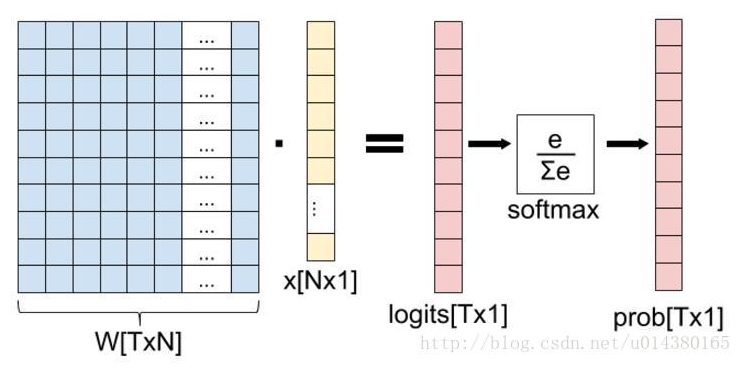
　　這張圖的等號左邊部分就是全連接層做的事，W是全連接層的參數，我們也稱為權值，X是全連接層的輸入，也就是特徵。從圖上可以看出特徵X是N*1的向量，這是怎麼得到的呢？這個特徵就是由全連接層前面多個卷積層和池化層處理後得到的，假設全連接層前面連接的是一個卷積層，這個卷積層的輸出是100個特徵（也就是我們常說的feature map的channel為100），每個特徵的大小是4*4，那麼在將這些特徵輸入給全連接層之前會將這些特徵flat成N*1的向量（這個時候N就是100*4*4=1600）。解釋完X，再來看W，W是全連接層的參數，是個T*N的矩陣，這個N和X的N對應，T表示類別數，比如你是7分類，那麼T就是7。我們所說的訓練一個網路，對於全連接層而言就是尋找最合適的W矩陣。因此全連接層就是執行WX得到一個T*1的向量（也就是圖中的logits[T*1]），這個向量裡面的每個數都沒有大小限制的，也就是從負無窮大到正無窮大。然後如果你是多分類問題，一般會在全連接層後面接一個softmax層，這個softmax的輸入是T*1的向量，輸出也是T*1的向量（也就是圖中的prob[T*1]，這個向量的每個值表示這個樣本屬於每個類的概率），只不過輸出的向量的每個值的大小範圍為0到1。

　　現在知道softmax的輸出向量的意思了，就是概率，該樣本屬於各個類的概率！

　　softmax 函數，又稱為歸一化指數函數。它是二分類函數 Sigmoid在多分類上的推廣，目的是將多分類的結果以概率的形式展現出來，下圖展示了softmax的計算方法：

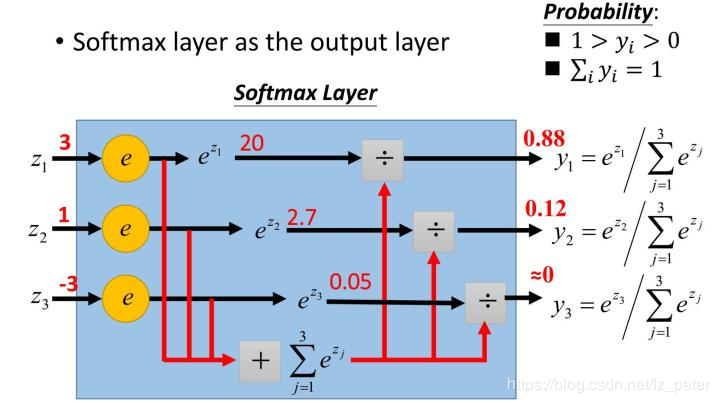
　　那麼為什麼softmax是這種形式呢？

　　首先，我們知道概率有兩個性質：1，預測的概率為非負數『2，各種預測結果概率之和等於1.

softmax 就是將在負無窮到正無窮上的預測結果按照這兩步轉換為概率的。

3.9.1 將預測結果轉化為非負數。

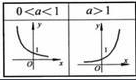
　　下圖是 y=exp(x) 的影像，我們可以知道指數函數的值域取值範圍是零到正無窮，softmax第一步就是將模型的預測結果轉化到指數函數上，這樣保證了概率的非負性。

3.9.2 各種預測結果概率之和等於1

　　為了確保各個預測結果的概率之和等於1，我們只需要將轉換後的結果進行歸一化處理。方法就是將轉化後的結果除以所有轉化後結果之和，可以理解為轉化後結果佔總數的百分比。這樣就得到了近似的概率。

　　簡單舉個例子：

　　假如模型對一個三分類問題的預測結果為-3、1.5、2.7。我們要用softmax將模型結果轉為概率。步驟如下：

　　1）將預測結果轉化為非負數

y1 = exp(x1) = exp(-3) = 0.05

y2 = exp(x2) = exp(1.5) = 4.48

y3 = exp(x3) = exp(2.7) = 14.88

　　2）各種預測結果概率之和等於1

z1 = y1/(y1+y2+y3) = 0.05/(0.05+4.48+14.88) = 0.0026

z2 = y2/(y1+y2+y3) = 4.48/(0.05+4.48+14.88) = 0.2308

z3 = y3/(y1+y2+y3) = 14.88/(0.05+4.48+14.88) = 0.7666

　　總結一下，softmax如何將多分類輸出轉換為概率，可以分為兩步：

1，分子：通過指數函數，將實數輸出映射到零到正無窮
2，分母：將所有結果相加，進行歸一化

　　下面是斯坦福大學 CS224n 課程中最 softmax的解釋：

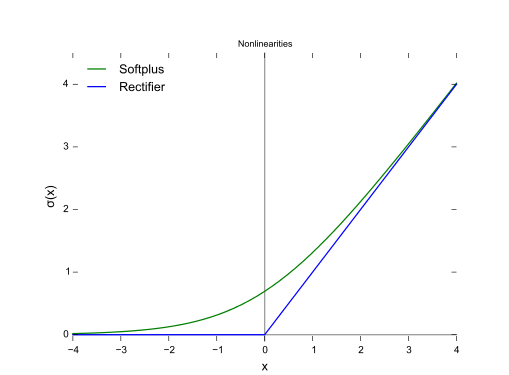
3.10 Softplus函數

　　函數如下：

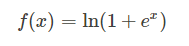
　　函數圖：

4，如何選擇合適的激活函數

　　一般我們可以這樣：

1，首先嘗試ReLU，速度快，但是要注意訓練的狀態
2，如果ReLU效果欠佳，嘗試Leaky ReLU 或者 Maxout 等變種
3，嘗試 tanh正切函數（以零為中心，零點處梯度為1）
4，Sigmoid tanh 在RMM（LSTM 注意力機制等）結構中有所應用，作為門控或者概率值
5，在淺層神經網路中，如不超過四層，可選擇使用多種激勵函數，沒有太大的影響

　　深度學習中往往需要大量時間來處理大量數據，模型的收斂速度是尤為重要的。所以，總體上來講，訓練深度學習網路盡量使用 zero-centered 數據（可以經過數據預處理實現）和 zero-centered 輸出。所以要盡量選擇輸出具有 zero-centered 特點的激活函數以加快模型的收斂速度。

　　如果是使用 ReLU，那麼一定要小心設置 learning rate，而且要注意，不要讓網路出現很多「dead」神經元，如果這個問題不好解決，那麼可以試試 Leaky ReLU ,PReLU , 或者 Maxout。

　　最好不要用 Sigmoid函數，不過可以試試 tanh，不過可以預期它的效果會比不上 ReLU和 maxout。

　　這篇筆記是整理網上優秀部落客的部落格，然後加上自己的理解，整理於此，主要是方便自己，方便別人查詢學習，僅此而已。

參考文獻：//my.oschina.net/u/876354/blog/1624376

//www.wandouip.com/t5i356161/

//blog.csdn.net/lz_peter/article/details/84574716

//www.bbsmax.com/A/QV5Zyg6nJy/

//www.cnblogs.com/ziytong/p/12820738.html

Tags: 深度學習常用演算法及筆記