演算法學習筆記:最近公共祖先(LCA問題)
- 2020 年 8 月 8 日
- 筆記
- 演算法----------, 演算法基礎:圖論
當我們處理樹上點與點關係的問題時(例如,最簡單的,樹上兩點的距離),常常需要獲知樹上兩點的最近公共祖先(Lowest Common Ancestor,LCA)。如下圖所示:

2號點是7號點和9號點的最近公共祖先
我們先來討論樸素的做法。
首先進行一趟dfs,求出每個點的深度:
int dep[MAXN];
bool vis[MAXN];
void dfs(int cur, int fath = 0)
{
if (vis[cur])
return;
vis[cur] = true;
dep[cur] = dep[fath] + 1; // 每個點的深度等於父節點的深度+1
for (int eg = head[cur]; eg != 0; eg = edges[eg].next)
dfs(edges[eg].to, cur);
}
現在A點的深度比B點深,所以我們先讓B點往上「爬」,爬到與A點深度相等為止。然後A點和B點再一起往上爬,直到兩點相遇,那一點即為LCA:
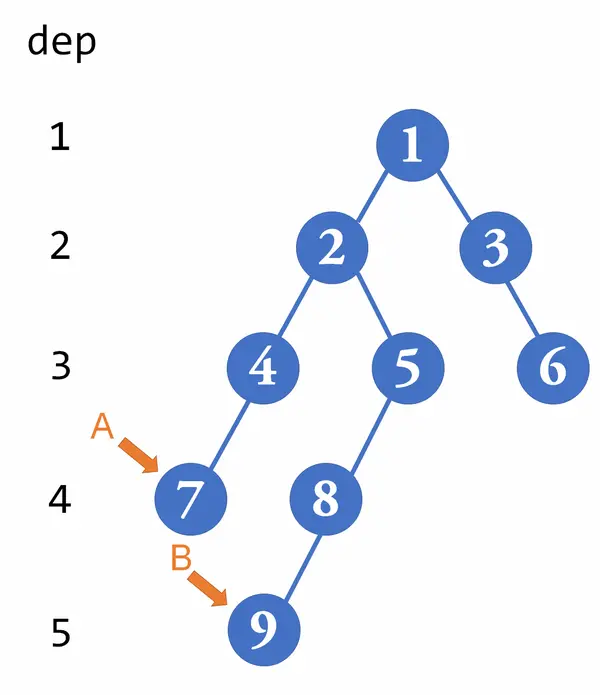
這樣下來,每次查詢LCA的最壞時間複雜度是 的。
有時候,我們需要進行很多次查詢,這時樸素的 複雜度就不夠用了。我們考慮空間換時間的倍增演算法。
倍增的思想直觀體現就在 ST表 中提及過。我們用一個數組fa[i][k]存儲 號點的
級祖先。(父節點為1級祖先,祖父結點為2級祖先……以此類推)
那麼這可以在dfs途中動態規劃得出:
// 在dfs中...
fa[cur][0] = fath;
for (int i = 1; i <= Log2[dep[cur]]; ++i) // Log2的預處理參見ST表的筆記
fa[cur][i] = fa[fa[cur][i - 1]][i - 1]; // 這個DP也參見ST表的筆記
這樣,往上爬的次數可以被大大縮短(現在變成「跳」了)。
首先還是先讓兩點深度相等:
if (dep[a] > dep[b]) // 不妨設a的深度小於等於b
swap(a, b);
while (dep[a] != dep[b]) // 跳到深度相等為止
b = fa[b][Log2[dep[b] - dep[a]]]; // b不斷往上跳
例如,a和b本來相差22的深度,現在b不用往上爬22次,只需要依次跳16、4、2個單位,3次便能達到與a相同的距離。
兩者深度相等後,如果兩個點已經相遇,那麼問題就得以解決。如果尚未相遇,我們再讓它們一起往上跳。問題在於,如何確定每次要跳多少?正面解決也許不太容易,我們逆向思考:如何在a、b不相遇的情況下跳到儘可能高的位置?如果找到了這個位置,它的父親就是LCA了。
說來也簡單,從可能跳的最大步數Log2[dep[a]](這樣至多跳到0號點,不會越界)開始,不斷減半步數(不用多次循環):
for (int k = Log2[dep[a]]; k >= 0; k--)
if (fa[a][k] != fa[b][k])
a = fa[a][k], b = fa[b][k];
以剛剛那棵樹為例,先嘗試Log2[4]=2,A、B點的 級祖先都是0(圖中未畫出),所以不跳。然後嘗試1,A、B的
祖先都是2,也不跳。最後嘗試0,A、B的1級祖先分別是4和5,跳。結束。
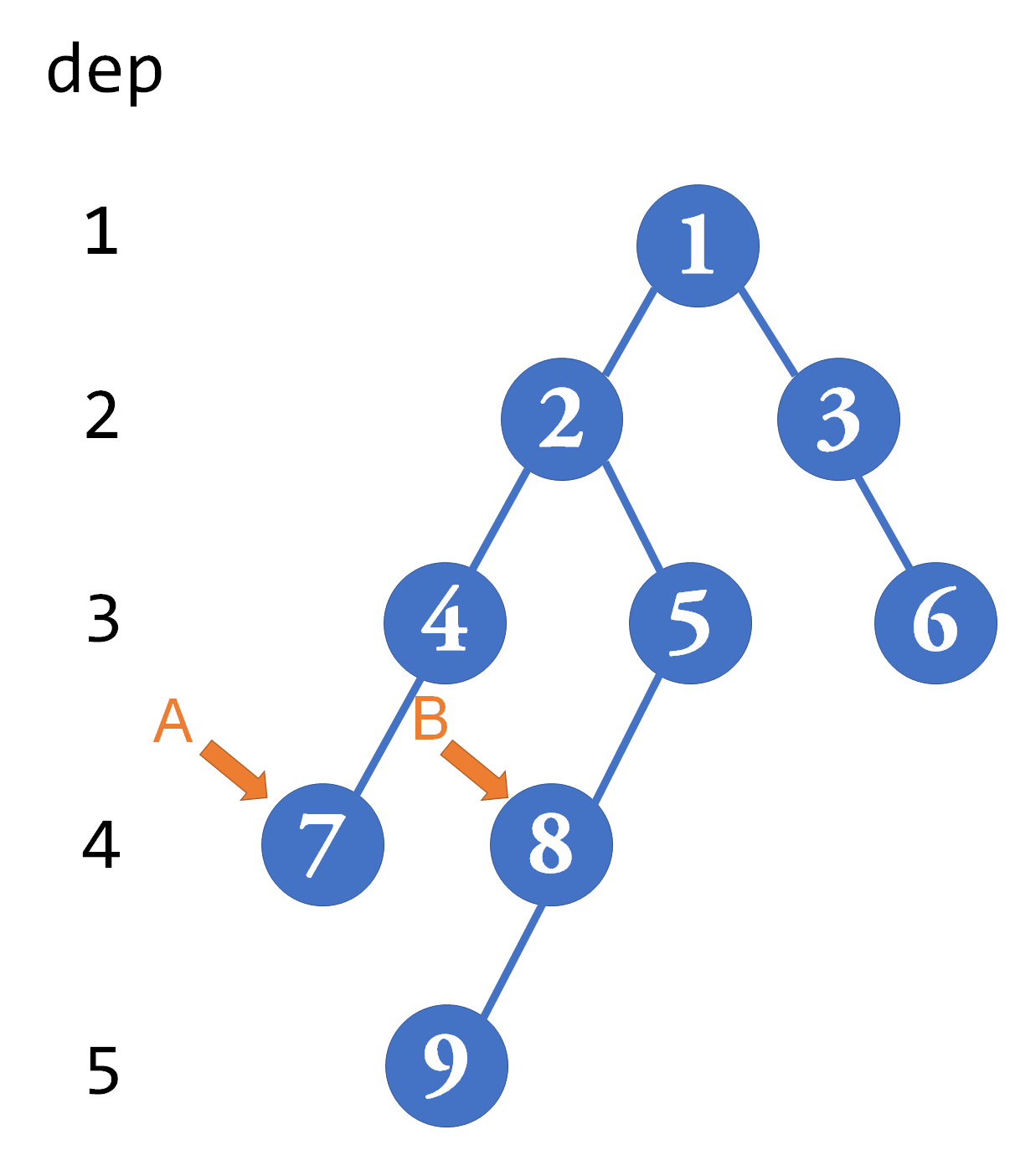
這樣下來,再往上一格所得到的2號點就是所求的最近公共祖先。
主要程式碼如下:
int Log2[MAXN], fa[MAXN][20], dep[MAXN]; // fa的第二維大小不應小於log2(MAXN)
bool vis[MAXN];
void dfs(int cur, int fath = 0)
{
if (vis[cur])
return;
vis[cur] = true;
dep[cur] = dep[fath] + 1;
fa[cur][0] = fath;
for (int i = 1; i <= Log2[dep[cur]]; ++i)
fa[cur][i] = fa[fa[cur][i - 1]][i - 1];
for (int eg = head[cur]; eg != 0; eg = edges[eg].next)
dfs(edges[eg].to, cur);
}
int lca(int a, int b)
{
if (dep[a] > dep[b])
swap(a, b);
while (dep[a] != dep[b])
b = fa[b][Log2[dep[b] - dep[a]]];
if (a == b)
return a;
for (int k = Log2[dep[a]]; k >= 0; k--)
if (fa[a][k] != fa[b][k])
a = fa[a][k], b = fa[b][k];
return fa[a][0];
}
int main()
{
// ...
for (int i = 2; i <= n; ++i)
Log2[i] = Log2[i / 2] + 1;
// ...
dfs(s); // 無根樹可以隨意選一點為根
// ...
return 0;
}
至於樹上兩點 的距離,有公式
(很好推)。
預處理,
查詢,空間複雜度為
。
當然,以上都是針對無權樹的,如果有權值,可以額外記錄一下每個點到根的距離,然後用幾乎相同的公式求出。


