圖演算法——狄克斯特拉演算法
- 2019 年 10 月 23 日
- 筆記
這裡有一些定義及程式碼取自CodeInfo的簡書,鏈接:https://www.jianshu.com/p/b805e9d1eb5c,和heroacool的CSDN,鏈接:https://blog.csdn.net/heroacool/article/details/51014824,感謝兩位大佬。
狄克斯特拉演算法(Dijkstra )用於計算出不存在非負權重的情況下,起點到各個節點的最短距離(單源最短路問題),如果要得到整個圖各個頂點之間的最短距離,則需要對整個圖的每個頂點都遍歷一遍狄克斯特拉演算法,顯然不合適,所以這裡要注意使用場合。
其思路為:
(1) 找出節點集合U裡面“最便宜”的節點,即可在最短時間內到達的節點,並將它加入集合S裡面(問題二:為什麼該節點可以加入S集合,也就是認為此時他與源節點距離最小),並把該節點從集合U裡面取出。
(2) 更新該節點對應的鄰居節點的開銷(問題一:其含義將稍後介紹)。
(3) 重複這個過程,直到對圖中的每個節點都這樣做了。
(4) 計算最終路徑。
為了防止重複遍歷節點,引進兩個集合S和U。S的作用是記錄已求出最短路徑的節點(以及相應的最短路徑長度),而U則是記錄還未求出最短路徑的節點(以及該節點到起點s的距離)。
由上可知,程式碼實現的時候要注意第一點即遍歷U集合裡面的最短路徑和第二點更新開銷。
問題一的見解:因為權重的賦予不同,所以並不會出現兩點之間直線最短。如下圖(自己畫的,有點丑),
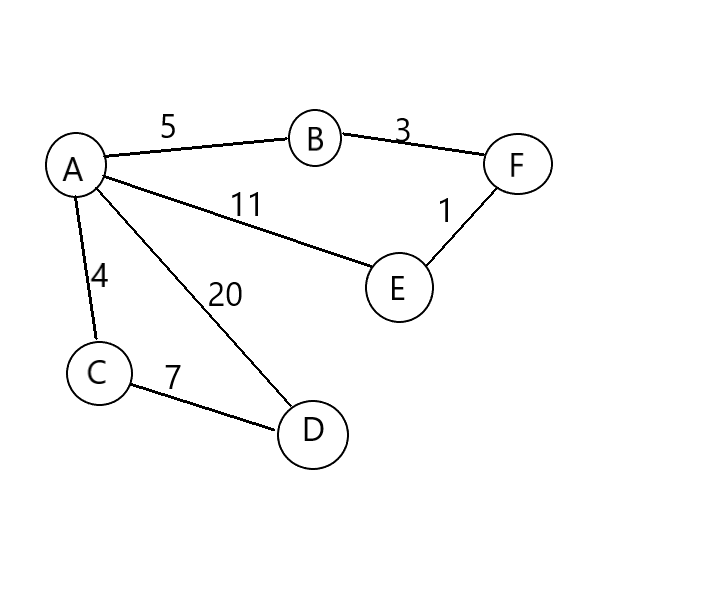
起點A->節點D的距離>起點A->節點C->節點D的距離,所以需要對不同節點到起點的開銷進行更新。但是問題又來了,如果每個點都把可以到達起點的所有路徑開銷進行更新,又會多出許多不必要的更新,我們要找的是最短路徑,如果比該節點到起點已知的開銷還要大的話,根本沒有比較的意義,而且作為最短路徑,那麼它前面的節點也就不會出現更短的情況,可以避免重複更新,減少不必要的重複,所以每次得到最短路徑的時候再進行更新就很有必要(問題的解的必要性)。那麼這樣子更新能否滿足問題的解的充分性呢?我們不妨這樣想,現在假設要通過節點C(這裡的節點C是上帝視角即整個完整圖裡面到達節點D最短路徑的前一個節點)到達節點D的距離會更短,要最短,那麼也就是起點A->節點C的距離1+節點C->節點D的距離2最短,易得距離1要在起點A->節點C的所有可能路徑中距離最短,所以每次找到最短路徑的節點時進行更新是合適的,如果的確存在這樣的路徑,就一定會有前一個節點(完整性)。
問題二的見解:這裡有點類似數學歸納法。
從第一個加入S集合的點說起,顯然該點就是起點,他到自己的距離為零。更新開銷後,各節點到起點距離不變。因為沒有負權重,所以這個時候距離起點最短的點shortest一定沒有其他路徑能夠提供更短距離到起點,即起點通過其他節點到達shortest的距離必然大於起點直接到達shortest,打個比方,起點A->shortest的距離為10,起點A->節點B的距離為12(該距離必然要大於起點A->shortest的距離,見藍字前提),又沒有負權重,所以起點A->shortest的距離<起點A->節點B->shortest的距離。所以將節點shortest加入集合S就沒有任何問題了。
現在有一個多於兩個節點的集合S,和集合U,提出這樣一個假設:當更新某個節點的開銷後,起點與集合U裡面的某個節點距離最短時,就認為這個距離是起點到該點所有路徑裡面最短的並且比起點到集合U其他節點的距離還要短。
shortest依舊是起點到集合U裡面各個節點最短距離的點。因為起點A->shortest的所有路徑裡面的最短距離的前一個節點必然開銷比shortest更小,也即是該節點在集合S裡面,所以這時候的起點A->shortest的距離是最短的。同時,對於集合U裡面的其他節點而言,起點A->他們的距離不可能比shortest更短(1,假設最短路徑的前一個節點在集合S裡面,那麼已經更新了;2,假設最短路徑的前一個節點在集合U裡面,無論這條路徑是怎麼走,必然會有一個節點C非起點,是集合S裡面的,不然該路徑上起點到其相鄰結點,此節點應在集合U裡面的距離將小於起點->shortest的距離)。
Java程式碼:
1 /** 2 * 狄克斯特拉演算法 3 * @author Administrator 4 * 5 */ 6 public class Dijkstra { 7 public static void main(String[] args){ 8 HashMap<String,Integer> A = new HashMap<String,Integer>(){ 9 { 10 put("B",5); 11 put("C",1); 12 } 13 }; 14 15 HashMap<String,Integer> B = new HashMap<String,Integer>(){ 16 { 17 put("E",10); 18 } 19 }; 20 HashMap<String,Integer> C = new HashMap<String,Integer>(){ 21 { 22 put("D",5); 23 put("F",6); 24 } 25 }; 26 HashMap<String,Integer> D = new HashMap<String,Integer>(){ 27 { 28 put("E",3); 29 } 30 }; 31 HashMap<String,Integer> E = new HashMap<String,Integer>(){ 32 { 33 put("H",3); 34 } 35 }; 36 HashMap<String,Integer> F = new HashMap<String,Integer>(){ 37 { 38 put("G",2); 39 } 40 }; 41 HashMap<String,Integer> G = new HashMap<String,Integer>(){ 42 { 43 put("H",10); 44 } 45 }; 46 HashMap<String,HashMap<String,Integer>> allMap = new HashMap<String,HashMap<String,Integer>>() { 47 { 48 put("A",A); 49 put("B",B); 50 put("C",C); 51 put("D",D); 52 put("E",E); 53 put("F",F); 54 put("G",G); 55 } 56 }; 57 58 59 Dijkstra dijkstra = new Dijkstra(); 60 dijkstra.handle("A","H",allMap); 61 } 62 63 private String getMiniCostKey(HashMap<String,Integer> costs,List<String> hasHandleList) { 64 int mini = Integer.MAX_VALUE; 65 String miniKey = null; 66 for(String key : costs.keySet()) { 67 if(!hasHandleList.contains(key)) { //找出未處理的點,即集合U裡面的點最小開銷 68 int cost = costs.get(key); 69 if(mini > cost) { 70 mini = cost; 71 miniKey = key; 72 } 73 } 74 } 75 return miniKey; 76 } 77 78 private void handle(String startKey,String target,HashMap<String,HashMap<String,Integer>> all) { 79 //存放到各個節點所需要消耗的時間 80 HashMap<String,Integer> costMap = new HashMap<String,Integer>(); 81 //到各個節點對應的父節點 82 HashMap<String,String> parentMap = new HashMap<String,String>(); 83 //存放已處理過的節點key,已處理過的不重複處理 84 List<String> hasHandleList = new ArrayList<String>(); 85 86 //首先獲取開始節點相鄰節點資訊 87 HashMap<String,Integer> start = all.get(startKey); 88 89 //添加起點到各個相鄰節點所需耗費的時間等資訊 90 for(String key:start.keySet()) { 91 int cost = start.get(key); 92 costMap.put(key, cost); 93 parentMap.put(key,startKey); 94 } 95 96 97 //選擇最"便宜"的節點,這邊即耗費時間最低的 98 String minCostKey = getMiniCostKey(costMap,hasHandleList); 99 while( minCostKey!=null ) { 100 System.out.print("處理節點:"+minCostKey); 101 HashMap<String,Integer> nodeMap = all.get(minCostKey); 102 if (nodeMap!=null) { 103 //該節點沒有子節點可以處理了,末端節點 104 handleNode(minCostKey,nodeMap,costMap,parentMap); 105 } 106 //添加該節點到已處理結束的列表中 107 hasHandleList.add(minCostKey); 108 //再次獲取下一個最便宜的節點 109 minCostKey = getMiniCostKey(costMap,hasHandleList); 110 } 111 if(parentMap.containsKey(target)) { 112 System.out.print("到目標節點"+target+"最低耗費:"+costMap.get(target)); 113 List<String> pathList = new ArrayList<String>(); 114 String parentKey = parentMap.get(target); 115 while (parentKey!=null) { 116 pathList.add(0, parentKey); 117 parentKey = parentMap.get(parentKey); 118 } 119 pathList.add(target); 120 String path=""; 121 for(String key:pathList) { 122 path = path + key + " --> "; 123 } 124 System.out.print("路線為"+path); 125 } else { 126 System.out.print("不存在到達"+target+"的路徑"); 127 } 128 } 129 130 private void handleNode(String startKey,HashMap<String,Integer> nodeMap,HashMap<String,Integer> costMap,HashMap<String,String> parentMap) { 131 132 for(String key : nodeMap.keySet()) { 133 //獲取原本到父節點所需要花費的時間 134 int hasCost = costMap.get(startKey); 135 //獲取父節點到子節點所需要花費的時間 136 int cost = nodeMap.get(key); 137 //計算從最初的起點到該節點所需花費的總時間 138 cost = hasCost + cost; 139 140 if (!costMap.containsKey(key)) { 141 //如果原本並沒有計算過其它節點到該節點的花費 142 costMap.put(key,cost); 143 parentMap.put(key,startKey); 144 }else { 145 //獲取原本耗費的時間 146 int oldCost = costMap.get(key); 147 if (cost < oldCost) { 148 //新方案到該節點耗費的時間更少 149 //更新到達該節點的父節點和消費時間對應的散列表 150 costMap.put(key,cost); 151 parentMap.put(key,startKey); 152 System.out.print("更新節點:"+key + ",cost:" +oldCost + " --> " + cost); 153 } 154 } 155 } 156 }
第63行的getMiniCostKey函數是用來計算起點A到集合U裡面距離最小節點。
第103行注釋指的是當nodeMap==null時,該節點沒有子節點可以處理了,末端節點,也就不用更新下一個結點的開銷了
第104行是handleNode(minCostKey,nodeMap,costMap,parentMap);函數用來更新開銷
第143行的parentMap使用一個key-value對來記錄路徑的最後節點及其父節點,這樣的話,通過遞推回去就能得到完整路徑
C語言程式碼:
1 // 鄰接矩陣 2 typedef struct _graph 3 { 4 char vexs[MAX]; // 頂點集合 5 int vexnum; // 頂點數 6 int edgnum; // 邊數 7 int matrix[MAX][MAX]; // 鄰接矩陣 8 }Graph, *PGraph; 9 10 // 邊的結構體 11 typedef struct _EdgeData 12 { 13 char start; // 邊的起點 14 char end; // 邊的終點 15 int weight; // 邊的權重 16 }EData; 17 ———————————————— 18 版權聲明:本文為CSDN部落客「heroacool」的原創文章,遵循 CC 4.0 BY-SA 版權協議,轉載請附上原文出處鏈接及本聲明。 19 原文鏈接:https://blog.csdn.net/heroacool/article/details/51014824
1 /* 2 * Dijkstra最短路徑。 3 * 即,統計圖(G)中"頂點vs"到其它各個頂點的最短路徑。 4 * 5 * 參數說明: 6 * G -- 圖 7 * vs -- 起始頂點(start vertex)。即計算"頂點vs"到其它頂點的最短路徑。 8 * prev -- 前驅頂點數組。即,prev[i]的值是"頂點vs"到"頂點i"的最短路徑所經歷的全部頂點中,位於"頂點i"之前的那個頂點。 9 * dist -- 長度數組。即,dist[i]是"頂點vs"到"頂點i"的最短路徑的長度。 10 */ 11 void dijkstra(Graph G, int vs, int prev[], int dist[]) 12 { 13 int i,j,k; 14 int min; 15 int tmp; 16 int flag[MAX]; // flag[i]=1表示"頂點vs"到"頂點i"的最短路徑已成功獲取。 17 18 // 初始化 19 for (i = 0; i < G.vexnum; i++) 20 { 21 flag[i] = 0; // 頂點i的最短路徑還沒獲取到。 22 prev[i] = 0; // 頂點i的前驅頂點為0。 23 dist[i] = G.matrix[vs][i];// 頂點i的最短路徑為"頂點vs"到"頂點i"的權。 24 } 25 26 // 對"頂點vs"自身進行初始化 27 flag[vs] = 1; 28 dist[vs] = 0; 29 30 // 遍歷G.vexnum-1次;每次找出一個頂點的最短路徑。 31 for (i = 1; i < G.vexnum; i++) 32 { 33 // 尋找當前最小的路徑; 34 // 即,在未獲取最短路徑的頂點中,找到離vs最近的頂點(k)。 35 min = INF; 36 for (j = 0; j < G.vexnum; j++) 37 { 38 if (flag[j]==0 && dist[j]<min) 39 { 40 min = dist[j]; 41 k = j; 42 } 43 } 44 // 標記"頂點k"為已經獲取到最短路徑 45 flag[k] = 1; 46 47 // 修正當前最短路徑和前驅頂點 48 // 即,當已經"頂點k的最短路徑"之後,更新"未獲取最短路徑的頂點的最短路徑和前驅頂點"。 49 for (j = 0; j < G.vexnum; j++) 50 { 51 tmp = (G.matrix[k][j]==INF ? INF : (min + G.matrix[k][j])); // 防止溢出 52 if (flag[j] == 0 && (tmp < dist[j]) ) 53 { 54 dist[j] = tmp; 55 prev[j] = k; 56 } 57 } 58 } 59 60 // 列印dijkstra最短路徑的結果 61 printf("dijkstra(%c): n", G.vexs[vs]); 62 for (i = 0; i < G.vexnum; i++) 63 printf(" shortest(%c, %c)=%dn", G.vexs[vs], G.vexs[i], dist[i]); 64 ———————————————— 65 版權聲明:本文為CSDN部落客「heroacool」的原創文章,遵循 CC 4.0 BY-SA 版權協議,轉載請附上原文出處鏈接及本聲明。 66 原文鏈接:https://blog.csdn.net/heroacool/article/details/51014824
可以看到狄克斯特拉演算法就是三件事,一,找到最短的點,二,把該點標記已處理,三,更新該點對其他點的影響。