RSA-演變過程、原理、特點（加解密及簽名）及公鑰私鑰的生成

  • 2019 年 10 月 22 日
  • 筆記

本篇是iOS逆向開發總結的第一篇文章，是關於iOS密碼學的相關技術分析和總結，希望對大家有所幫助，如果有錯誤地方歡迎指正。

一、前言

密碼學的歷史追溯到2000年前，相傳古羅馬凱撒大帝為了防止敵方截獲情報，用密碼傳送情報。凱撒大帝的做法比較簡單，通過對二十幾個羅馬字母表建立一張對應的表格，這樣如果不知道密碼，截獲也會沒有用。

 

 

在1976年前，所有的加密方法都是同一種模式：加密、解密使用同一種演算法。在數據交互的時候，彼此通訊雙方就必須將規則告訴對方，否則就沒法解密。加密和解密的規則也就是密鑰，保護它尤為顯得重要，傳遞密鑰就成了最大的隱患。這種加密方式被稱為對稱加密演算法。

1977年有三位麻省理工學院的數學家羅納德.李維斯特（Ron Rivest）、阿迪.薩默爾（Adi Shamir）和倫納德.阿德曼（Leonard Adleman）一起設計了演算法，可以實現非對稱加密。這個演算法就是用三個人的名字命名，叫做RSA演算法

RSA加密方式比較特殊，需要兩個密鑰：公開密鑰簡稱公鑰（publickey）和私有秘鑰簡稱私鑰（privatekey）。公鑰加密，私鑰加密；私鑰加密，公鑰解密。這個演算法就是偉大的RSA演算法。

  • RSA加密或者簽名後的結果都是不可逆的二進位，使用時大部分都會轉換為BASE64碼再傳輸。
  • RSA加密時，對要加密的數據大小有限制，最大不大於密鑰的長度。列如在使用1024bit的密鑰時（genrsa -out rsa_private_key.pem 1024），最大可以加密到1024/8 = 128Bytes的數據。數據大於128Bytes時，此時就需要對數據進行分組加密–因為數據超限，加解密就會失效，openssl會返回false ，分組加密之後的加密串拼接成一個字元串後發送到客戶端。
  • 為了保證每次加密的結果都不相同，RSA加密時在待加密數據之後拼接一個隨機字元串，然後再進行加密。不同的填充方式Padding表示字元串的不同長度，在對超限數據進行分組之後，會按照Padding指定的長度添加到隨機字元串。列如Padding填充方式使用默認OPENSSL_PKCS1_PADDING（需要佔用11個位元組用於填充）那麼這樣明文長度最多就是128-11=117Bytes。
  • 接收方解密也需要分組。將加密後的原始二進位數據每128 Bytes分為一組中，然後再進行解密，解密之後，根據Padding的長度進行丟棄隨機字元串，把得到的原字元串拼接起來，就得到原始報文。

 

二、RSA原理

RSA演算法的可靠性基礎： 對極大整數做因數分解是很困難的。

RSA是非對稱演算法，加解密使用不同的密鑰。

兩個密鑰都是可以用於加密，解密時需要另一個密鑰。但是，通常用公鑰加密，私鑰進行解密，因為公鑰是公開的。理論上A和B之間通過RSA實現保密通訊，需要A和B各自生成一組密鑰來，同時保管好自己的私鑰；而用對方的公鑰加密要發送的消息，用自己的私鑰解密對方發過來的消息。

在簽名的場景下，用私鑰進行簽名，公鑰驗證。

RSA比DES等對稱加密要慢的多。一般在實際傳輸數據時，用RSA加密比較短的對稱密碼，雙方交換密碼後再使用DES等對稱演算法傳輸數據。

 

2.1 歐拉函數

歐拉函數: 求小於N的正整數中與N互質的數的個數

例如: 對應5, 與5互質的數總共有1,3,也就是φ(N) = 2。

RSA演算法是運用歐拉函數一個特例,如果N可以分解成兩個互質的整數的積: N = pq

則: φ(N) = φ(p)φ(q) = (p−1)(q−1)

例如: φ(35947) = φ(103)φ(349) = (103−1)(349−1)=35496

 

2.2 模反元素

兩個正整數a和n互質,那麼一定能找到整數b,使得ab -1 被n來整除,也就是ab ≡ 1 (mod n)

這時侯,b被叫做a的模反元素

 

RSA加密過程:

  1. 取兩個質數p1,p2
  2. 確定了n值,n = p1 * p2, n值一般會很大程度為1024個二進位位;
  3. 確定φ(n),這樣φ(n)=(p1-1) * (p2-1);
  4. 確定e值,1<e<φ(n)，e為整數而且與φ(n)互質;
  5. 確定d值,e*d%φ(n)=1;
  6. 加密 c = m^e%n;
  7. 解密 m=c^d%n

實際的驗證:

  1. p1 = 3, p2 = 7;
  2. n = p1 * p2 = 3 * 7 = 21;
  3. φ(n)=(p1-1) * (p2-1)=2*6=12;
  4. 1 < e < 12, e = 5 (12 與 e互質則取值{1,5,7,11}, φ(12) = 4)
  5. e * d % φ(n) = 5 * d % 12 = 1,則d =17
  6. 設置明文 m = 3, 則 c = m ^ e % n = 3 ^ 5 % 21 = 12
  7. 解密密文 m = c ^ d % n = 12 ^ 17 % 21 = 3

下面是數據傳輸過程圖解:

 

三、OpenSSL

openSSL是蘋果系統內置的開源加密庫,這樣我們就可以通過終端來獲取私鑰公鑰,進行數據加密.

主要命令:

　　1. 生成RSA私鑰

openssl genrsa -out private.pem 1024

　　2. 從私鑰中提取出公鑰

openssl rsa -in private.pem -pubout -out public.pem

　　3. 將私鑰轉換成為明文

openssl rsa -in private.pem -text -out private.txt

　　4. 經過公鑰進行加密

openssl rsautl -encrypt -in message.txt -inkey public.pem -pubin -out enmsg.txt

　　5. 經過私鑰進行解密

openssl rsautl -decrypt -in enmsg.txt -inkey private.pem -out demsg.txt

　　6. 經過私鑰進行加密

openssl rsautl -sign -in message.txt -inkey private.pem -out enmsg2.txt

　　7. 經過公鑰進行解密

openssl rsautl -verify -in enmsg2.txt -inkey public.pem -pubin -out demsg2.txt

 

終端使用:

　　1.創建公鑰私鑰

 

　　2. 查看私鑰公鑰

 

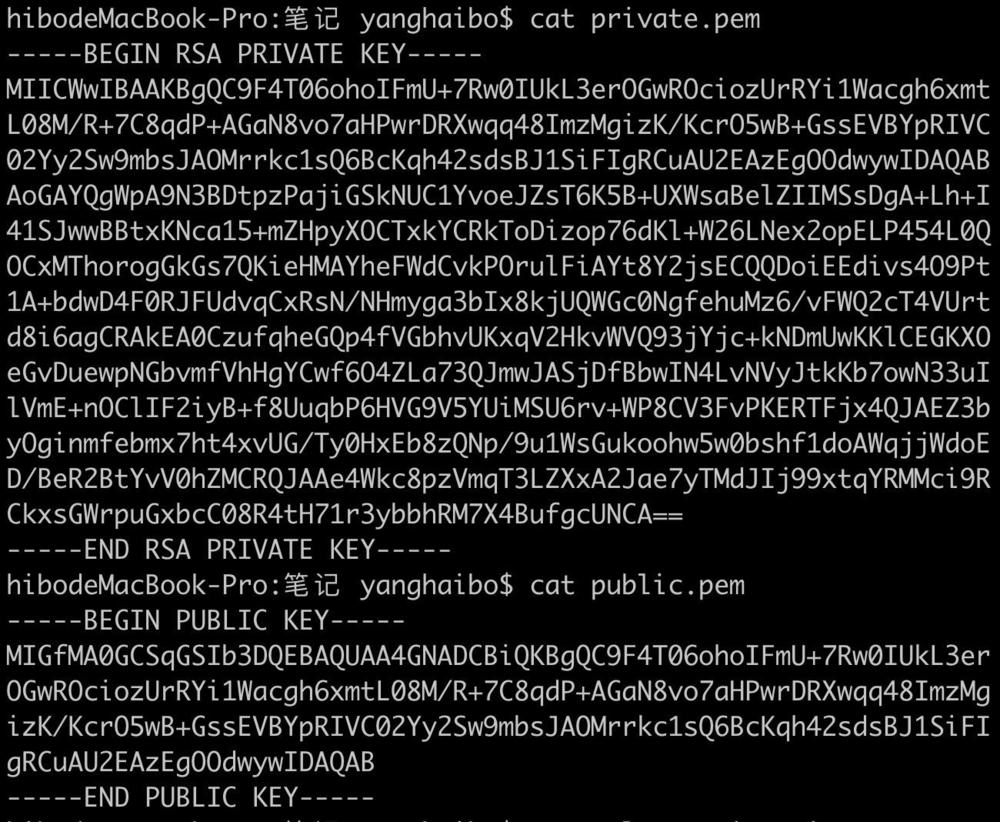
　　3.創建文本

 

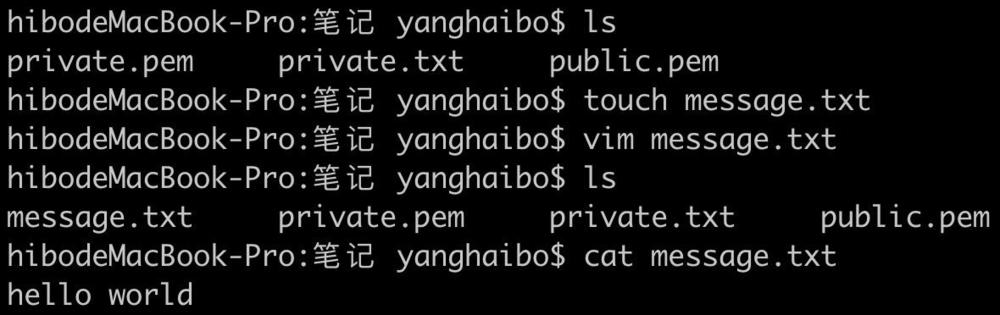
　　4. 公鑰加密

 

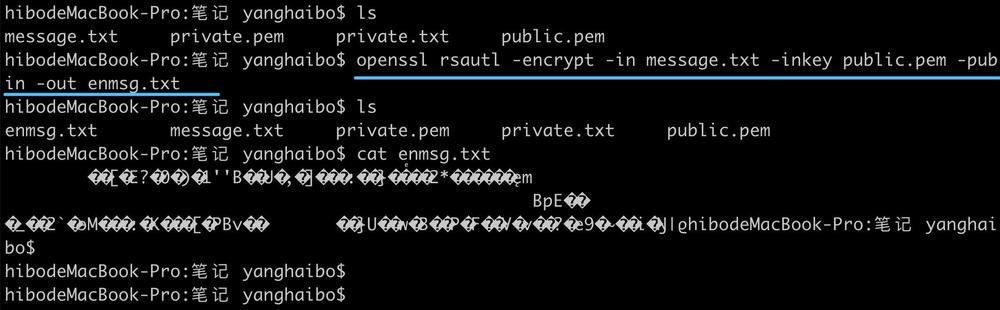
　　5. 私鑰解密

 

　　6. 私鑰加密

 

　　7. 公鑰解密

 

通過上面的7種方式,得到如下結果圖解:

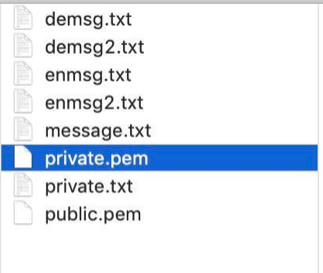
大家可以通過終端嘗試上面的命令,用起來撒!!!

 

以後就是關於RSA的基本講解,希望對大家有所幫助!!!下一篇將講解哈希演算法在逆向的使用!

VirMach 便宜 VPS

QNews

QNews