小話數據結構-圖 (聚焦與於實現的理解)
數學使我們能夠發現概念和聯繫這些概念的規律,這些概念和規律給了我們理解自然現象的鑰匙。
——愛因斯坦
前言
本文程式碼基於C++實現,閱讀本文,需要有以下知識
-
教熟練使用C++ STL庫中的vector,map,pair等;
-
對於遞歸和簡單搜索演算法(dfs,bfs)有粗淺的理解;
-
稍微的離散數學或者是線性代數知識(可能是我瞎掰的,沒有也罷 😂 )
本文針對演算法或數據結構初學者(比如我)寫下,本人不才,如有錯誤請輕噴 😄 。
瓶頸
在學習「數據結構」這門課之前,「圖論」這個略顯高級的辭彙看起來還與我那麼的遙遠,在經過了「離散數學」的學習之後,我慢慢認識到其實數據結構就是離散數學模型的程式碼實現,並且在不斷的學習中,我開始能以我自己的思維去理解圖論的知識。
數據結構的教科書上,每個知識點都會系統的從「定義——術語——存儲結構——相關操作」娓娓道來,然而,各種各樣的障礙阻礙著我們認知的過程。對於離散數學不熟悉的,一時間無法抽象出模型,教材上冗長的程式碼實現,給讀者一種晦澀難懂的感覺。這時候我們就要思考離散數學的本質——將具體問題抽象為一般問題,在由演算法解決。因此,我們在一開始不必過於在意方法,而是應該聚焦與實現,像大學物理做實驗一樣,多操作幾遍,自然就熟能生巧,甚至開發出新的理解。
你得從用戶的體驗出發,推倒用什麼技術。 ——喬布斯在1997年回歸蘋果發布會上回答提問
案例-引入
什麼是圖?簡單說就是點與點之間的網狀關係。
比如以下有6個城市之間的鐵路線。
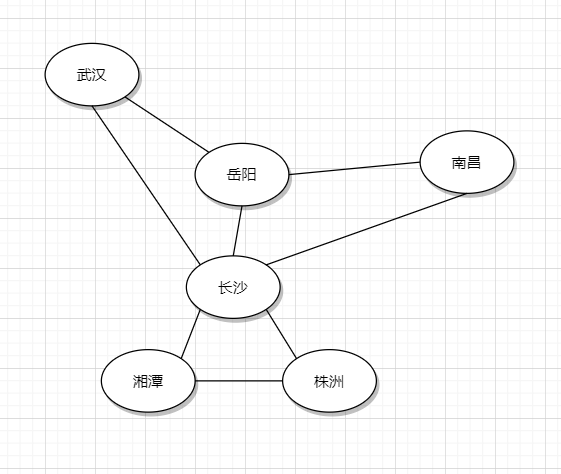
地圖就是一個很經典的圖
那麼,我們是如何表達他們的關係的呢
我們使用鄰接表or鄰接矩陣
為什麼是鄰接表/矩陣
鄰接表和鄰接矩陣是圖的兩種常用存儲表示方式,用於記錄圖中任意兩個頂點之間的連通關係,包括權值。
(在圖論相關的案例中,我們會特別頻繁的用到這兩種表示方式)
我們不談什麼二元組三元組的,想想啊,圖重要的頂多就仨玩意:節點,邊,權值,而使用鄰接表和鄰接矩陣已經可以清晰簡潔的表達這些關係了。
我們先看看鄰接表和鄰接矩陣怎麼建;
鄰接表
emm,用圖表示就是上面那張圖啊,程式碼實現的話,我們用stl的vector更方便一點
#include <iostream> #include <vector> struct edge{//邊資訊,邊有啥屬性往裡丟就行 int to;//該邊可以去往的下一個節點編號,有明確指向,是單向邊。 int value;//存邊的權值,如果沒有可以直接忽略 edge(int t,int v) :to(t), value(v){};//構造函數 }; vector<edge> node[n];//用vector實現鄰接表的存儲 //ps:邊資訊只有一個可以直接存int,兩個可以用stl的pair,三個及以上就肯定要用struct了 //vector<int> node[n],vector<pair<int, int> >都是可行的,自己清楚意思就行
這裡是什麼意思呢,就是我有n個vector數組,每一個數組表示一個點的資訊,vector里存的是邊(edge),每一個點到點的通路意味著有一個對應的edge資訊。
那麼,如何把資訊存入鄰接表呢,我們假設用一下流程輸入(大概就是平時做題的時候題目要求的輸出啦)
先假設每條邊的權值都是一樣的,就設為「1」吧
//第一行為兩個整數n,e,分別表示節點數,邊數,隨後n行,輸入節點資訊,在隨後e行,接受邊資訊
6 8
武漢 岳陽 南昌 長沙 株洲 湘潭
武漢 岳陽
岳陽 南昌
武漢 長沙
南昌 長沙
岳陽 長沙
長沙 株洲
長沙 湘潭
湘潭 株洲
#EOF
那麼,在C語言裡面我們這麼處理輸入
map<string,int> tab; map<int,string> tab0; //建立散列表(哈希表),使每個城市的編號和名字可以相互連接 int n,m; cin>>n>>m; for(int i=0;i<n;i++){ string name; cin>>name; tab0.insert({i,name}); tab.insert({name,i}); //給每一個城市編號 } while(m--){ edge tmp; string a,b; node[map[a]].push_back(edge(map[b],1)); //構造函數中map[a]表示名為a的城市對應的編號,1表示權值,存入vector數組g中 node[map[b]].push_back(edge(map[a],1)); //因為是雙向邊所以正向反向都存一遍 }
這樣的話,我們的鄰接表就完全存儲好了
對於任意一個點,我們要遍歷其相鄰點,只需要用一下程式碼
//輸入城市名字 輸出其相鄰所有城市的名字 string name; cin>>name; for(auto it=node[tab[name]].begin();it!=g[tab[name]].begin();it++){//遍歷name節點的所有邊 cout<<tab0[it->to]<<endl; }
假如我們輸入
岳陽
那麼就會返回
武漢
南昌
長沙
整個鄰接表的存儲和訪問過程就是以上的樣子了
鄰接矩陣
這個就很好理解了,就是一個n*n的二維數組模擬矩陣,表達的是點與點之間的關係,我們沿用上一個例子里的輸入,我們建立出來的矩陣大概是這樣
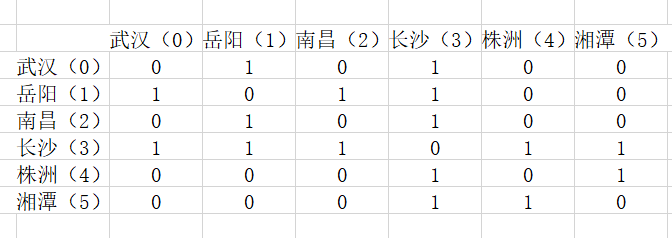
這個鄰接矩陣只是判定有無直接相連的,我們用一個6*6的二維數組可以很輕鬆的建出來,沒有自旋,未聯通和自我比較設置為0(false),已聯通即設置為1(true)。
案例-常見問題
(PS:本人才疏學淺,只介紹部分案例的大致思維路線,細節歡迎各位深入思考)
我們接著上一個案例看,對於很多情況,鄰接矩陣像上面這樣,就算建出來了,但是我們現在用的,是一個實實在在的生活中的例子,誰都直到武漢和南昌之間必定可以通過鐵路線到達,只是會經過別的站台。
這個時候就引出了一個問題,按照鄰接表來看,武漢和南昌實際上是通過其他的節點連接起來了的,只是沒有直接連接。
然而此時,從「武漢「到」南昌」實際上有多條線路
武漢->岳陽->南昌
武漢->長沙->南昌
武漢->長沙->岳陽->南昌
武漢->岳陽->長沙->南昌
武漢->長沙->湘潭->株洲->南昌
………………
那我們給其付的權值到底是2,3,4還是多少呢?
這就可以引入到一個常見的圖論問題——「最短路」了
最短路
(PS:最短路問題在演算法競賽和數學建模競賽中都是非常常見的)
故名思意,當我們想要直接去往某個目的地時,一定是講究時間效率的,我們不願意走太長,更不願意繞圈子,用規範的話說就是:「找最短路,並且避免系統資源浪費」,那我們就要先走一遍所有路徑,看看哪個路徑可行(好比每天高鐵第一班車是「探路車」)。
假設我們要從武漢出發,去南昌:
我們從武漢開始遍歷武漢接下來可以到達每一個城市
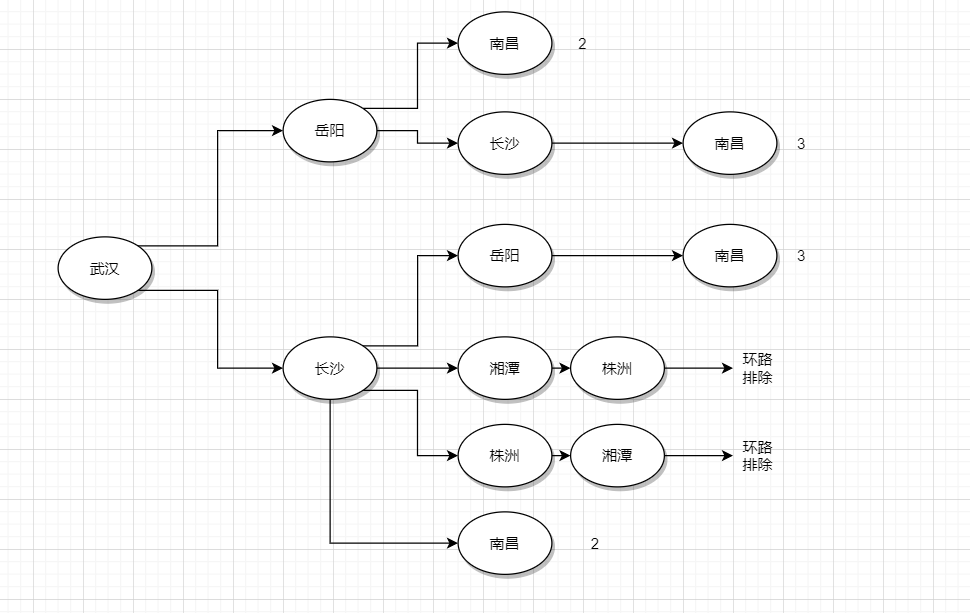
如此以來,逐個分析每個為直接相連的點,我們可以得到整個圖的帶權值的的鄰接矩陣表示,其中有一個要點,即點不能重複訪問,而BFS按照層次遍歷鄰接表的模式非常契合這個目的。我們沿用上方的輸入和鄰接表的存儲形式,以下給出大致的偽程式碼:
#include<queue>//stl的queue容器 void bfs(int st){ queue<edge> qu;//創建隊列 qu.push(起始狀態入隊); while(!qu.empty()){//當隊列非空 if(當前狀態x方向可走) qu.push(當前狀態->x);//該狀態入隊 if(當前狀態向y方向可走) qu.push(當前狀態->y);//該狀態入隊 ………………… 處理(隊頂)qu.top(); 相應操作; qu.pop();//隊首彈出隊 }//一次循環結束,執行下一次循環 }
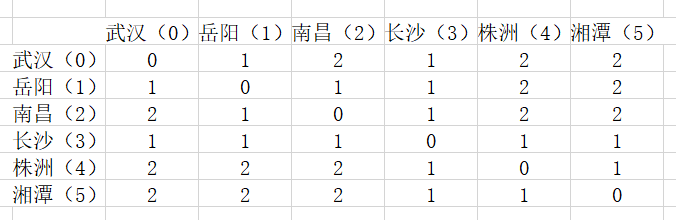
如此以來,我們就得到了整個圖,每個節點的詳細資訊,可以根據需求進行更細節的操作。
這便是最短路的基本思想,當然,實際情況會更加複雜,比如邊的權值各有不同,是有向邊,出現負權值等情況,也會有相應的演算法(迪特斯科拉,貝爾曼-福德,弗洛伊德,SPFA,A_Star等演算法),同時,在圖的遍歷時,通過鄰接矩陣我們也可以瞥見連通圖的很多性質,優美的現象能吸引人的思考,數學之美就在於這些奇妙之處。
歐拉路
我們有目的性出行,肯定也有旅遊出行,肯定有人喜歡欣賞沿途的風景,我舉個例子,加入有一個岳陽人,他很喜歡看火車沿路的風景,他把以上6個城市作為了自己旅行可規劃的目的地,他想在各個路線中穿梭,路線越長越好,但是他不喜歡看重複的風景,他想規劃一個走過的路不重複,而且最長的路線。走過的路不重複,就是所謂的歐拉路。
因為我們著重考慮路徑,所以使用之前判定有無直接連接的鄰接矩陣就可以了,我們使用DFS來遍歷所有邊並找出最長的一條。
int g[N][N];//鄰接矩陣2維數組 //默認鄰接矩陣資訊已經存入了該二維數組中 bool st[N][N];//標記某一條邊是否被訪問過 int ans;//存儲答案 void dfs(int start, int res) { for (int i = 0; i < n; i++) { if (g[start][i] == 1 || st[start][i] || st[i][start]) //該邊可以通過並且是第一次通過 continue; st[u][i] = st[i][u] = true;//標記 dfs(i, res + 1);//下一步 st[u][i] = st[i][u] = false;//回溯 } ans = max(ans, res);//保證得到最大的結果 }
歐拉(回)路問題其實就是經典的「一筆畫問題」,應為我們每一步的判定和操作都是固定的,通過dfs的「自相性」我們往往能簡潔而優美的解決這一系列問題。
為了繼續思考圖論的模型,我們接下來不使用程式碼討論另外兩種模型,這兩種模型的程式碼模板很方便理解,了解了基本思路和模型,就很方便應用了。
並查集
我們都知道每個省有很多地放,現在隨意給你兩個市區的名稱,想要你判斷以下他們是否屬於同一個省份。
我們將每個城市存入其數據結構,可以得出以下的情況
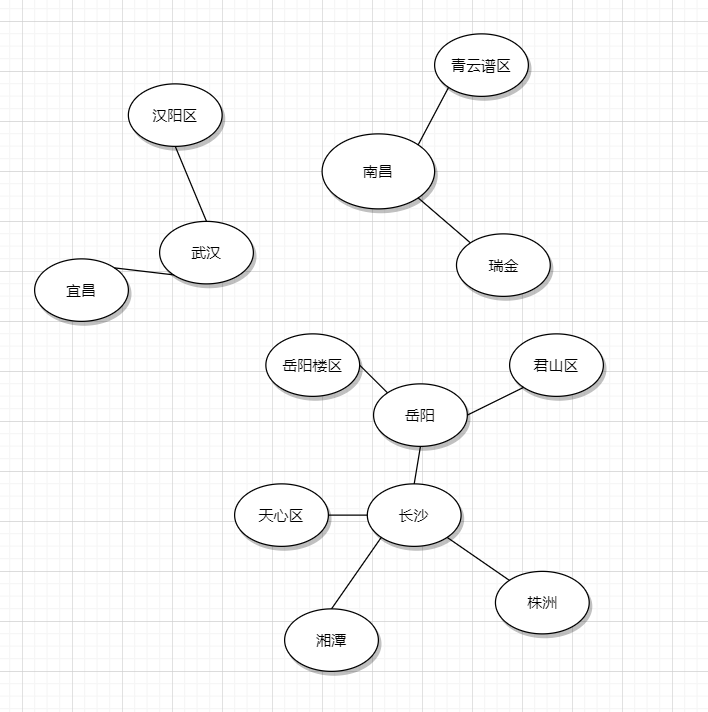
並查集的關鍵在於處理父子節點的關係,這樣的數據架構可以處理大量的「集合合併」操作
最小生成樹
再來一個例子,假設我們要再部分城市之間架設最新最快的交通軌道,為了使成本最低,現在要你選出一個方案,使架設的軌道線路最低:(現在我們給邊附上權值)
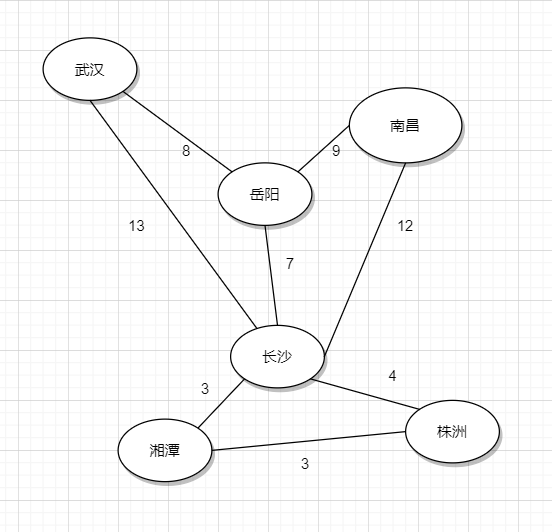
這樣便是一個基礎的無向圖最小生成樹問題,我們根據我們已經建立的關係,採用並查集的數據結構,採用Kruskal或者Prim演算法的模板可以求出以下結果
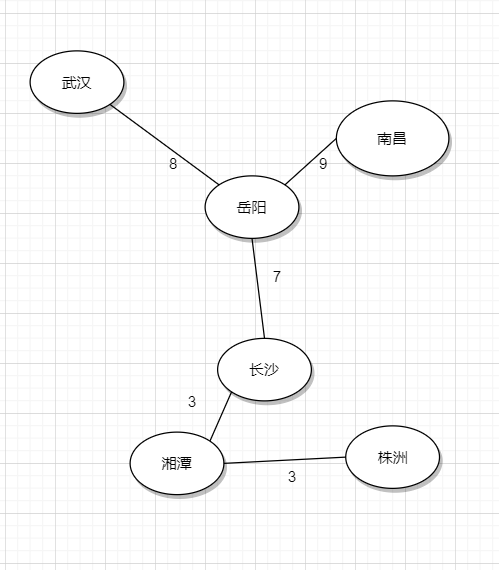
更多……
圖論的問題和每一個節點的資訊息息相關,而如何使用圖論模型,關鍵在於如何定義「節點」。
關於這個問題,我很喜歡《演算法圖解》里的講解方式——將「狀態」轉化為「資訊」儲存到「節點」里,每個狀態是一個「節點」,狀態變化的過程就是「邊」。這便是連接實際問題和圖論演算法的橋樑,理解了這個思想,很多模型建立的困惑就能迎刃而解了,圖論的其他問題基本都能通過這個思想來建模。
希望我的拋磚引玉能引起更多的思考! 😄 (蒟蒻鞠躬)。


