AVL樹(查找、插入、刪除)——C語言
- 2019 年 10 月 3 日
- 筆記
AVL樹
平衡二叉查找樹(Self-balancing binary search tree)通常是指一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1,並且任意節點的左右兩個子樹都是一棵平衡二叉樹(即嚴格的平衡二叉查找樹,“嚴格”二字體現在任意節點的左右子樹高度差不超過1),平衡二叉樹有多種實現方法(紅黑樹、AVL、替罪羊樹、Treap、伸展樹等)本篇隨筆分析的AVL樹(AVL樹是根據它的發明者G. M. Adelson-Velskii和E. M. Landis命名的),是在二叉查找樹的基礎上一個優化版本(AVL樹是嚴格的二叉查找樹,而紅黑樹不是,紅黑樹是非嚴格的二叉查找樹,紅黑樹有自己的一套規則來保證整棵樹接近平衡)
AVL樹的特點:
1.本身首先是一棵二叉查找樹
AVL樹的作用
AVL樹解決了二叉查找樹可能出現的極端情況,對於一般的二叉搜索樹(Binary Search Tree),其期望高度(即為一棵平衡樹時)為log2n,其各操作的時間複雜度(O(log2n))同時也由此而決定,但是在某些極端情況下
(如在插入的序列是有序的時),二叉搜索樹將退化成近似鏈或鏈,此時,其操作的時間複雜度將退化成線性的,即O(n)。我們可以通過隨機化建立二叉搜索樹來盡量的避免這種情況,但是在進行了多次的操作之後,例如在在刪除時,
我們總是選擇將待刪除節點的後繼代替它本身,這樣就會造成總是右邊的節點數目減少,以至於樹向左偏沉。這同時也會造成樹的平衡性受到破壞,使得它的操作時間複雜度增加
例如下面這種情況:
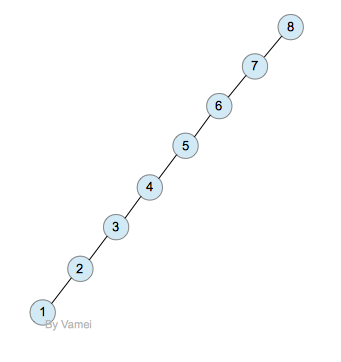
AVL樹的特性讓二叉搜索樹的節點實現平衡(balance):節點相對均勻分布,而不是偏向某一側
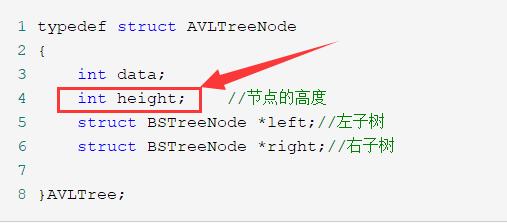
AVL樹節點的定義:
1 typedef struct AVLTreeNode 2 { 3 int data; 4 int height; //節點的高度 5 struct BSTreeNode *left;//左子樹 6 struct BSTreeNode *right;//右子樹 7 8 }AVLTree;
與一般的二叉查找樹的節點相比多了一個參數,節點的高度(網上有些部落格是把平衡因子加在了節點的定義裡面,筆者不太建議這樣做)
預備知識
為了讀者能更好了理解AVL樹的操作,在繼續往下看之前需要搞清楚幾個概念
高度、深度和平衡因子
(1)深度——從上往下數

(樹的深度 = 葉子節點的深度)
(2)高度——從下往上數
關於高度,有的文章中將”空二叉樹的高度定義為-1″,本篇隨筆採用維基百科上的定義:空二叉樹的高度為0,因為高度是從下往上數,所以葉子節點的高度為1
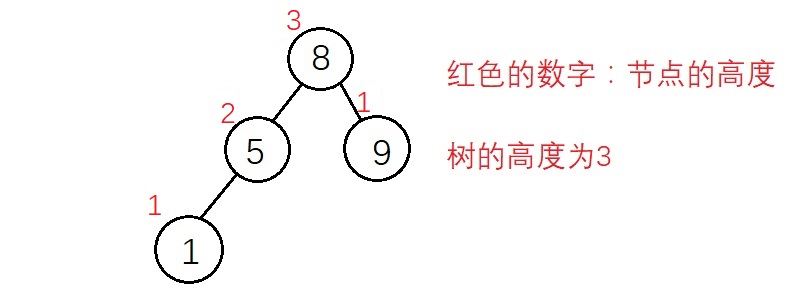
(樹的高度 = 根節點的高度)
(3)平衡因子
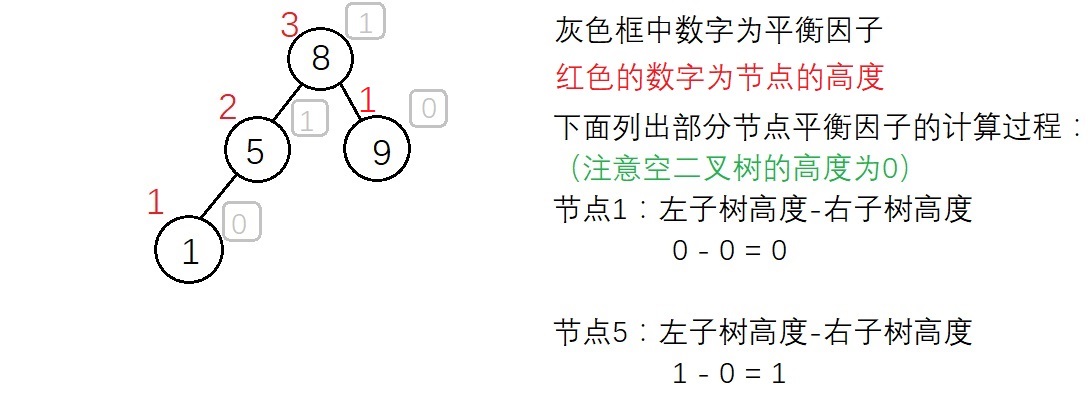
(平衡因子計算時左子樹 – 右子樹 和 右子樹 – 左子樹 都可以,因為判斷樹是否平衡的條件是:每個結點的左右子樹的高度之差的絕對值不超過1,只不過判斷失衡以後還要判斷是哪一種失衡,這就需要根據情況來選擇是左-右還是右-左了)
—————————————————————————————————–
1、查找節點
在 AVL樹 中查找與在 二叉查找樹 中查找完全一樣,因為AVL樹總是保持平衡的,樹的結構不會由於查詢而改變,這裡就不再贅述了
實現程式碼:

1 /* 查找特定值 */ 2 void SearchData(int targ, BSTree *nod) 3 { 4 if (nod != NULL) 5 { 6 if (nod->data == targ) 7 { 8 printf("查找值存在,值為%dn", nod->data); 9 } 10 else if (nod->data > targ) 11 { 12 SearchData(targ, nod->left); //遞歸查找左子樹 13 } 14 else if (nod->data < targ) 15 { 16 SearchData(targ, nod->right); //遞歸查找右子樹 17 } 18 } 19 else if (nod == NULL) 20 { 21 printf("查找值不存在n"); 22 } 23 }
View Code
2、插入節點(遞歸實現)
先梳理一下步驟

先來實現搜索最低失衡節點,搜索最低失衡節點是從新插入的節點(也就是葉子節點)往上搜索(也可以說成從新增結點開始向根部回溯),搜索到的第一個平衡因子>1(|左子樹高度-右子樹高度|>1)的節點,作為最低失衡節點,因為是從新插入的節點往上搜索,二叉樹的搜索是單向的(結構體成員中只有左右子樹),單獨使用一個函數來實現逆向搜索實現起來並不方便,這裡就把搜索最低失衡節點的操作放到遞歸實現的插入操作中
這裡沒有像上一篇隨筆:二叉查找樹(查找、插入、刪除)——C語言那樣先手動輸入的一個二叉平衡樹(因為這裡要考慮節點的高度,輸入不太方便),乾脆就從空二叉樹開始插入
實現程式碼:
/* 獲取節點高度,空樹的高度為0 */ int GetNodeHeight(AVLTree *nod) { if (nod != NULL) //若不為空子樹 { if (nod->left == NULL && nod->right == NULL) //若為葉子節點 { return 1; } else if (GetNodeHeight(nod->right) > GetNodeHeight(nod->left)) //若右子樹高度較高 { return (nod->right)->height + 1; } else //若左子樹高度較高 { return (nod->left)->height + 1; } } else //若為空子樹 { return 0; } } /* 添加新節點(包含搜索最低失衡節點和調整樹操作) */ AVLTree *AddNewNode(AVLTree *nod, int NewData) { AVLTree *p = NULL; if (nod == NULL) { if ((nod = (AVLTree *)malloc(sizeof(AVLTree))) == NULL) //創建新節點 { printf("記憶體不足"); exit(0); } nod->data = NewData; nod->left = NULL; nod->right = NULL; nod->height = GetNodeHeight(nod); } else if (NewData > nod->data) { nod->right = AddNewNode(nod->right, NewData); nod->height = GetNodeHeight(nod); if (GetNodeHeight(nod->right) - GetNodeHeight(nod->left) > 1) //右子樹高度 - 左子樹高度 { } return nod; } else if (NewData < nod->data) { nod->left = AddNewNode(nod->left, NewData); nod->height = GetNodeHeight(nod); if (GetNodeHeight(nod->left) - GetNodeHeight(nod->right) > 1) //左子樹高度 - 右子樹高度 { } return nod; } else if (NewData == nod->data) { printf("不允許插入重複值"); exit(0); } return nod; }
(若二叉樹中只有根節點,那麼這個根節點也是葉子節點)
在上面的程式碼中已經實現了插入新節點並且搜索最低失衡節點的功能,這裡可以用前序遍歷二叉樹並列印節點高度來判斷插入節點函數是否正確(上面預留的調整二叉樹函數的位置)
遍歷二叉樹:
1 /* 前序遍歷AVL樹,並列印節點高度 */ 2 void PreOrder_Traverse(AVLTree *nod) 3 { 4 if (nod != NULL) 5 { 6 printf("data = %d height = %dn", nod->data, nod->height); 7 8 PreOrder_Traverse(nod->left); 9 PreOrder_Traverse(nod->right); 10 } 11 }
測試插入函數(保證每次插入新節點後的二叉樹都是二叉平衡樹)

測試數據圖解:
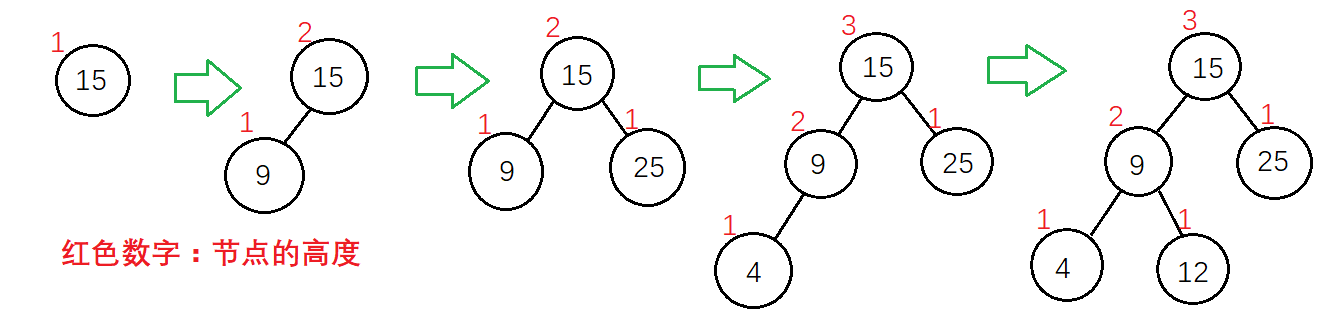
測試結果:

搞清楚了各個節點的高度,平衡因子的計算也比較方便了,下面就是AVL樹的核心操作“旋轉”,不同的失衡情況有不同的旋轉方式,一共有四種節點失衡情況,如下圖

不同失衡情況下的示例二叉樹,如下圖(讀者可能會發現“最低失衡節點的左子樹的左子樹還有非空節點”這個判斷依據,對第二組圖適用,但對於第一組圖不太合適)
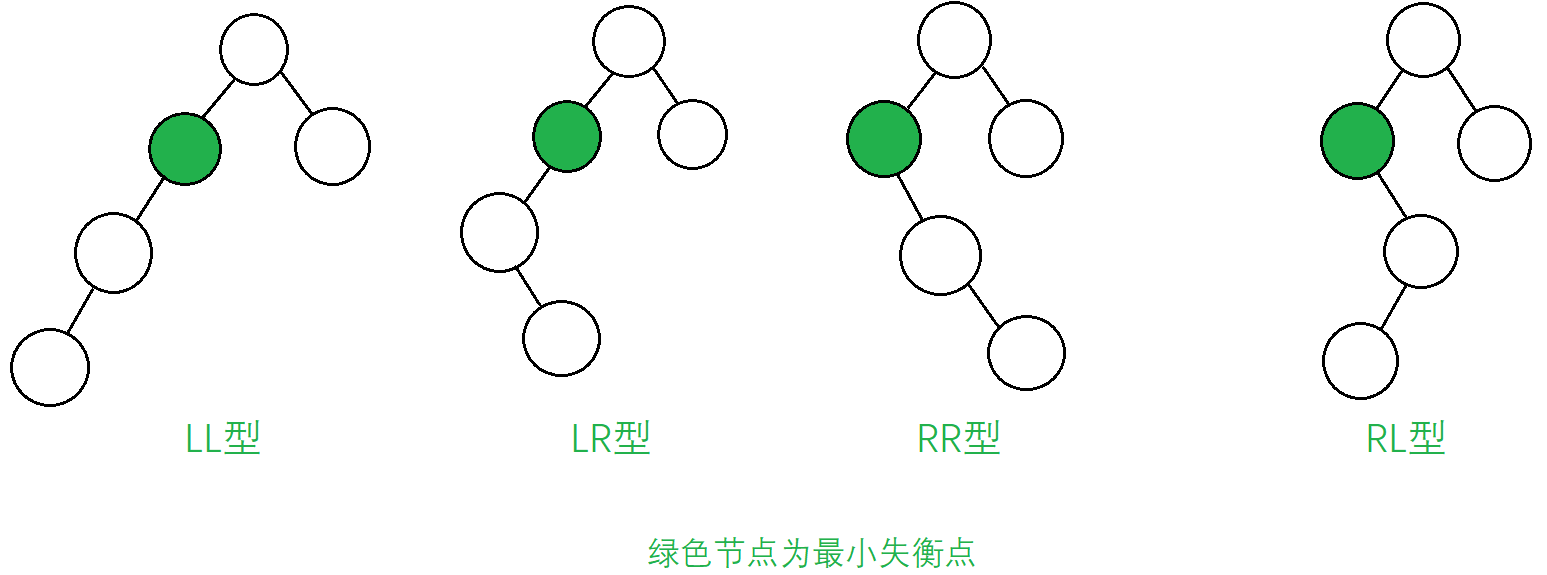
或者是
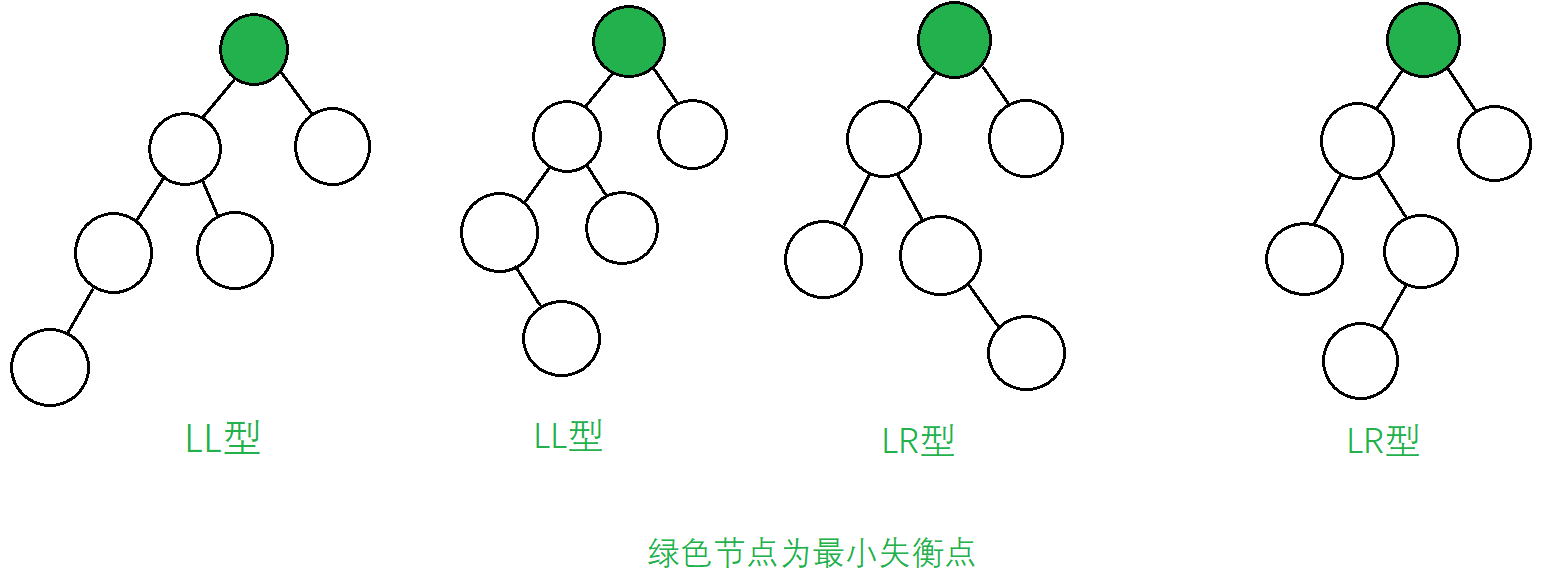
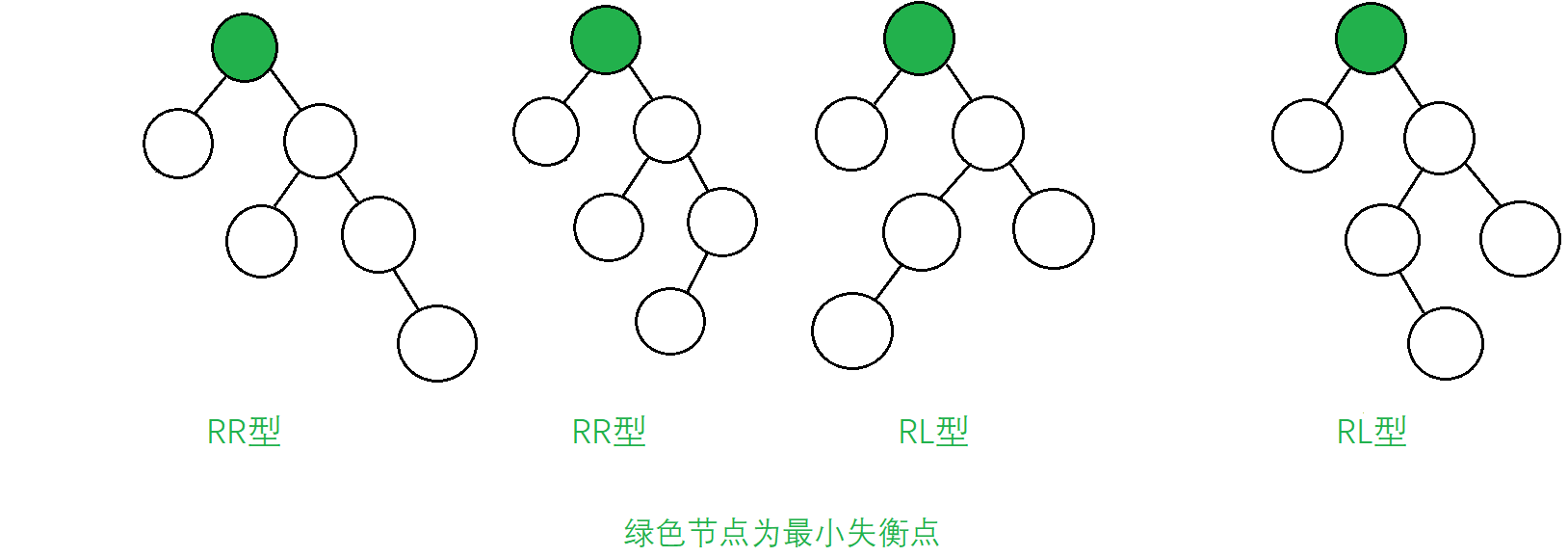
(LL型和RR型的操作相對簡單)
第一種:LL型
LL型失衡,調整二叉樹需要兩步
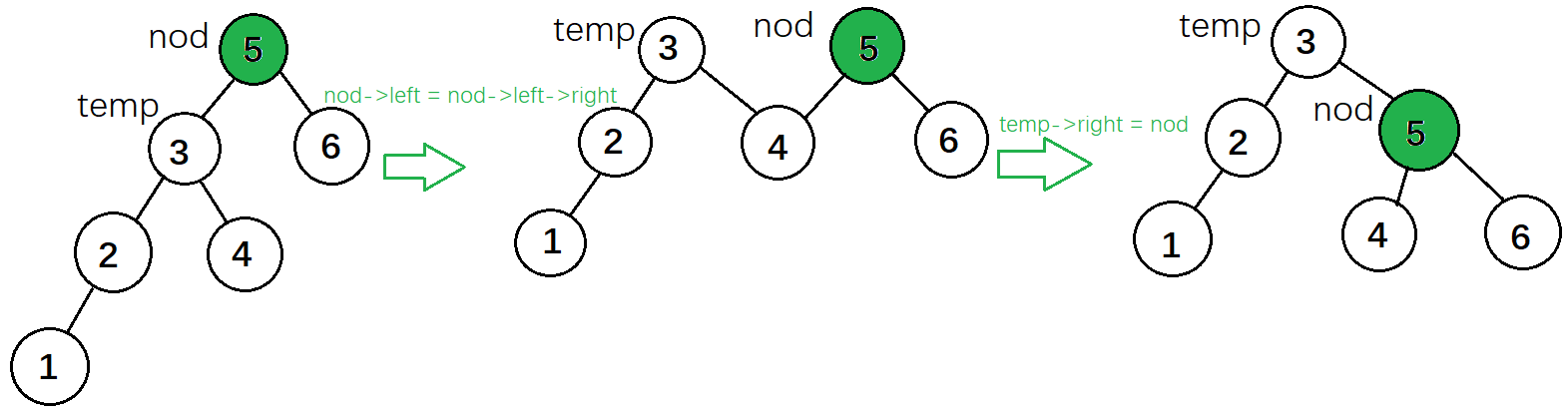
第一步:將失衡節點的左子樹的右子樹 變成 失衡節點的左子樹
第二步:失衡節點 變成 失衡節點未發生操作前左子樹的右子樹
只看上面的敘述有點繞,下面為實現程式碼和圖片示例
實現程式碼:
1 /* LL型旋轉 */ 2 AVLTree * LL_Rotation(AVLTree *nod) 3 { 4 AVLTree *temp; 5 temp = nod->left; //臨時保存nod的左子樹 6 7 nod->left = nod->left->right; //將失衡節點的左子樹的右子樹 變成 失衡節點的左子樹 8 temp->right = nod; //失衡節點 變成 temp的右子樹 9 10 nod->height = GetNodeHeight(nod); //更新節點高度 11 temp->height = GetNodeHeight(temp); 12 13 return temp; 14 }
LL型旋轉圖解
GIF圖:
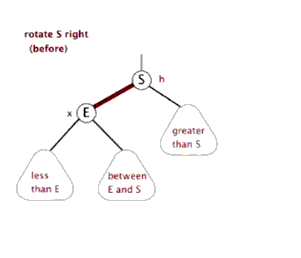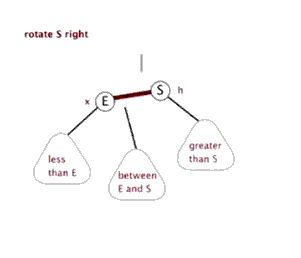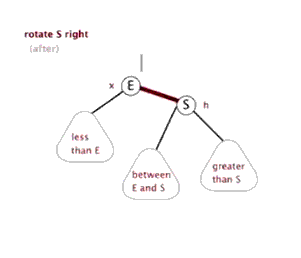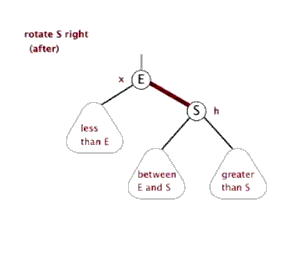
(圖片來源:http://www.sohu.com/a/270452030_478315)
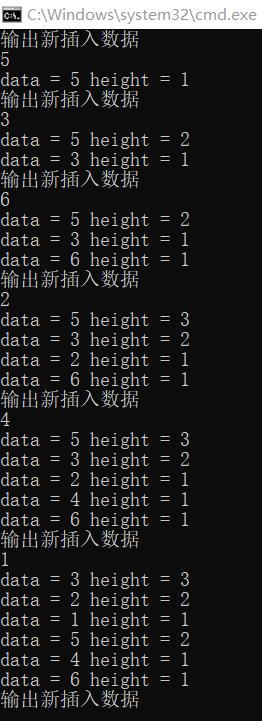
LL型失衡測試:
測試數據:

測試結果:
第二種:RR型
RR型的操作和基本相同,只是方向相反,這裡就不再贅述了
實現程式碼:

1 /* RR型旋轉 */ 2 AVLTree * RR_Rotation(AVLTree *nod) 3 { 4 AVLTree *temp; 5 temp = nod->right; //臨時保存nod的右子樹 6 7 nod->right = nod->right->left; 8 temp->left = nod; 9 10 nod->height = GetNodeHeight(nod); //更新節點高度 11 temp->height = GetNodeHeight(temp); 12 13 return temp; 14 }
View Code
第三種:LR型
LR型失衡的操作相比於LL型失衡操作相對要複雜一點,需要旋轉兩次才能恢復平衡
第一步:對失衡節點的左子樹進行RR型旋轉
第二步:對失衡節點進行LL型旋轉
因為之前已經寫好了LL型和RR型的旋轉,這裡直接用就可以了,實現程式碼如下
1 /* LR型旋轉 */ 2 AVLTree * LR_Rotation(AVLTree *nod) 3 { 4 nod->left = RR_Rotation(nod->left); 5 nod = LL_Rotation(nod); 6 7 return nod; 8 }
LR型旋轉圖解:
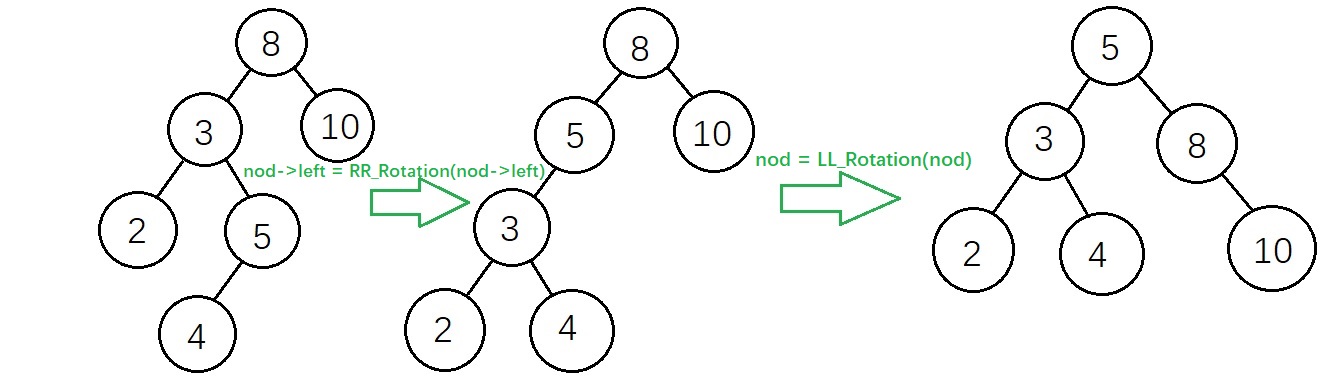
測試數據:

第三種:RL型
和LR型的旋轉基本相同,這裡就不再贅述了,實現程式碼如下

1 /* RL型旋轉 */ 2 AVLTree * RL_Rotation(AVLTree *nod) 3 { 4 nod->right = LL_Rotation(nod->right); 5 nod = RR_Rotation(nod); 6 7 return nod; 8 }
View Code
3、刪除節點
刪除節點比插入節點的操作還要稍微複雜一點,因為插入時,進行一次平衡處理(一次平衡處理可能包含多次旋轉),整棵樹都會處於平衡狀態,而在刪除時,需要進行多次平衡處理,才能保證樹處於平衡狀態
AVL樹的刪除操作前半部分和二叉查找樹相同,只不過刪除後要檢查樹是否失去平衡,如果失衡就需要重新調整平衡,並更新節點高度,總的來說可以分為如下幾種情況
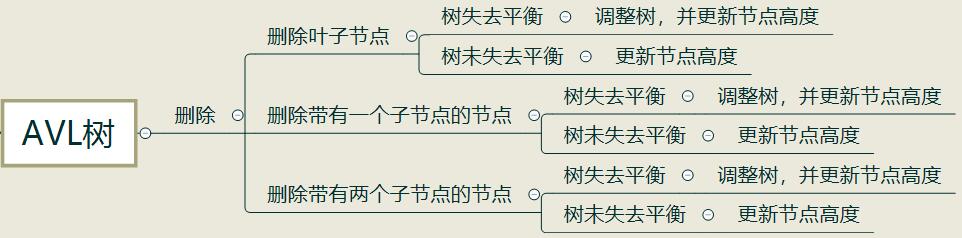
(1)刪除葉子節點
情況一:刪除節點後二叉樹沒有失去平衡
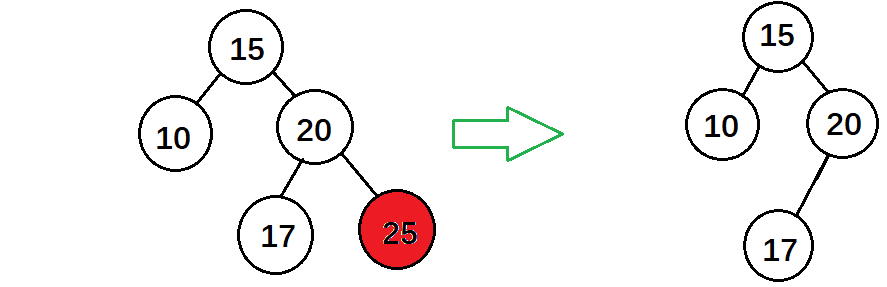
刪除節點後樹沒有失去平衡,這種情況下只需要更新節點的高度
情況二:刪除節點後二叉樹失去平衡

上圖的RE型失衡只有在刪除操作時才可能出現(在插入時不可能出現),RE型失衡的旋轉方式和RR型失衡的旋轉方式一模一樣
(雖然刪除節點時遇到的失衡情況多了兩種 LE和RE ,但是旋轉的方式依舊是那四種(LL、RR、LR、RL))
實現程式碼:
1 /* 刪除節點 */ 2 AVLTree *DeletNode(AVLTree *nod, int DelData) 3 { 4 AVLTree *SNode = NULL; //後繼節點 5 AVLTree *PSNode = NULL; //後繼節點的父節點 6 AVLTree *temp = NULL; //臨時保存待釋放節點的子樹,避免free後找不到左右子樹 7 8 if (nod == NULL) 9 { 10 printf("刪除節點不存在"); 11 exit(0); 12 } 13 else if (DelData > nod->data) 14 { 15 nod->right = DeletNode(nod->right, DelData); 16 17 if (GetNodeHeight(nod->left) - GetNodeHeight(nod->right) > 1) 18 { 19 temp = nod->left; 20 21 if (GetNodeHeight(temp->left) >= GetNodeHeight(temp->right)) //LL型或LE型失衡、兩種情況處理方式相同 22 { 23 nod = LL_Rotation(nod); 24 } 25 else //LR型失衡 26 { 27 nod = LR_Rotation(nod); 28 } 29 } 30 31 nod->height = GetNodeHeight(nod); //更新節點高度 32 } 33 else if (DelData < nod->data) 34 { 35 nod->left = DeletNode(nod->left, DelData); 36 37 if (GetNodeHeight(nod->right) - GetNodeHeight(nod->left) > 1) 38 { 39 temp = nod->right; 40 41 if (GetNodeHeight(temp->right) >= GetNodeHeight(temp->left)) //RR或RE型失衡、兩種情況處理方式相同 42 { 43 nod = RR_Rotation(nod); 44 } 45 else //RL型失衡 46 { 47 nod = RL_Rotation(nod); 48 } 49 } 50 51 nod->height = GetNodeHeight(nod); //更新節點高度 52 } 53 else if (DelData == nod->data) 54 { 55 if (nod->right == NULL && nod->left == NULL) //若待刪除節點為葉子節點 56 { 57 free(nod); 58 return NULL; 59 } 60 }
(2)刪除帶有一個子節點的節點
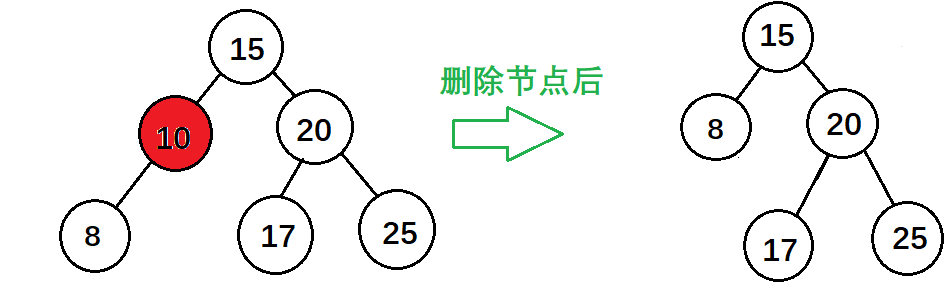
1 else if (DelData == nod->data) 2 { 3 if (nod->right == NULL && nod->left == NULL) //若待刪除節點為葉子節點 4 { 5 free(nod); 6 return NULL; 7 } 8 else if (nod->right == NULL && nod->left != NULL) //若待刪除節點只有左子樹 9 { 10 temp = nod->left; 11 free(nod); 12 13 return temp; 14 } 15 else if (nod->right != NULL && nod->left == NULL) //若待刪除節點只有右子樹 16 { 17 temp = nod->right; 18 free(nod); 19 20 return temp; 21 } 22 }
(3)刪除帶有兩個子節點的節點
刪除帶有兩個子節點的節點時,需要找到待刪除的節點的後繼節點或者前驅節點(本篇隨筆使用後繼節點),具體方法在上一篇隨筆已經列出“二叉查找樹(查找、插入、刪除)——C語言”,這裡不再贅述
1 else //若待刪除節點既有左子樹也有右子樹 2 { 3 SNode = SearchSuccessorNode(nod->right); //搜索後繼節點 4 PSNode = SearchParentofSNode(nod->right, nod->right); //搜索後繼節點的父節點 5 6 if (nod->right == SNode) //後繼節點為待刪除節點的右子樹(後繼節點有右子樹和沒有右子樹的操作相同) 7 { 8 SNode->left = nod->left; 9 free(nod); 10 11 return SNode; 12 } 13 else if (nod->right != SNode && SNode->right == NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點沒有右子樹 14 { 15 SNode->left = nod->left; 16 SNode->right = nod->right; 17 PSNode->left = NULL; 18 free(nod); 19 20 return SNode; 21 } 22 else if (nod->right != SNode && SNode->right != NULL) //後繼節點不為待刪除節點的右子樹,並且該後繼節點有右子樹 23 { 24 25 PSNode->left = SNode->right; //後繼節點的右子樹作為後繼節點父節點的左子樹 26 SNode->left = nod->left; 27 SNode->right = nod->right; 28 free(nod); 29 30 return SNode; 31 } 32 } 33 }
需要注意的是,刪除節點時不會出現“後繼節點不是刪除節點的子節點,且後繼節點有右子樹”這種情況,如下圖
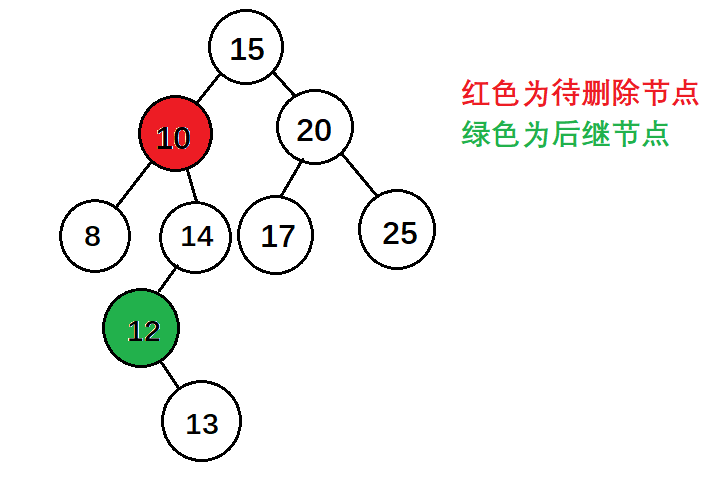
上圖的14節點已經失衡了,在插入的時候就會被調整,所以不會出現“後繼節點不是刪除節點的子節點,且後繼節點有右子樹”這種情況
(由於筆者能力有限,AVL樹的刪除操作分析的不是很清楚,若有疏漏,清指出)

