機器學習筆記簿降維篇 LDA 01

2020 年 7 月 29 日
筆記
機器學習-降維篇

機器學習中包含了兩種相對應的學習類型：無監督學習和監督學習。無監督學習指的是讓機器只從數據出發，挖掘數據本身的特性，對數據進行處理，PCA就屬於無監督學習，因為它只根據數據自身來構造投影矩陣。而監督學習將使用數據和數據對應的標籤，我們希望機器能夠學習到數據和標籤的關係，例如分類問題：機器從訓練樣本中學習到數據和類別標籤之間的關係，使得在輸入其它數據的時候，機器能夠把這個數據分入正確的類別中。線性鑒別分析（Linear Discriminant Analysis, LDA）就是一個監督學習演算法，它和PCA一樣是降維演算法，但LDA是陣對於分類問題所提出的。

1. 一個投影的LDA

設訓練樣本矩陣為\(X=[x_1,x_2,\cdots,x_n]\in \mathbb R^{m\times n}\)，其中樣本向量\(x_j\in\mathbb R^m(j=1,2,\cdots,n)\)。假設樣本被分為\(c\)個類，編號為\(1,2,\cdots,c\)，定義屬於第\(i\)個類的樣本的集合為\(X_i\)，第\(i\)個類的樣本個數為\(N_i\)。我們首先定義第\(i\)個類樣本的均值為

\[\mu_i=\frac{1}{N_i}\sum_{x\in X_i}x
\]

所有樣本的均值為

\[\mu=\frac1n\sum_{j=1}^nx_j
\]

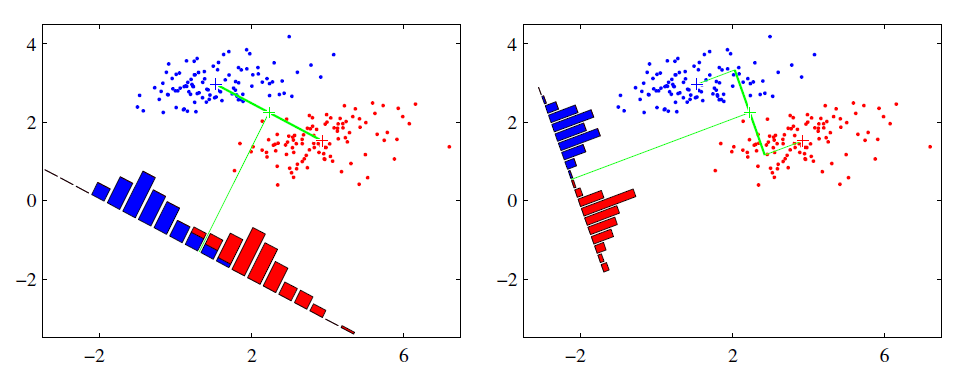
LDA的原理基於Fisher鑒別準則（Fisher Discriminant Criterion），這個準則做出了一個假設：投影后的樣本集合，類間散度最大、類內散度最小，其意義在於讓投影之後，類和類之間的距離盡量拉開，但是類中的個樣本盡量聚集在一起，這就是LDA能夠解決分類問題的精髓。設投影向量為\(w\in\mathbb R^m\)，那麼投影后樣本的類間散度可以用總均值和各個類的均值的方差來表示：

\[\begin{eqnarray*}
&&\max_{w}\sum_{i=1}^cN_i\left(w^T\mu_i-w^T\mu\right)^2\\
&=&\max_{w}\sum_{i=1}^cN_iw^T(\mu_i-\mu)(\mu_i-\mu)^Tw\\
&=&\max_{w}w^T\left[\sum_{i=1}^cN_i(\mu_i-\mu)(\mu_i-\mu)^T\right]w\tag1\\
\end{eqnarray*}\\
\]

同理，類內散度是每一個類中的樣本方差之和：

\[\begin{eqnarray*}
&&\min_w\sum_{i=1}^c\sum_{x\in X_i} \left(w^Tx-w^T\mu_i\right)^2\\
&=&\min_w\sum_{i=1}^c\sum_{x\in X_i}{w^T(x-\mu_i)(x-\mu_i)^Tw}\\
&=&\min_w{w^T\left[\sum_{i=1}^c\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T\right]w}\tag{2}
\end{eqnarray*}
\]

因此，為了方便表示，我們定義類間散度矩陣\(S_b\)和類內散度矩陣\(S_w\)：

\[{
S_b=\sum_{i=1}^cN_i(\mu-\mu_i)(\mu-\mu_i)^T\\
S_w=\sum_{i=1}^c\sum_{x\in X_i}(x-\mu_i)(x-\mu_i)^T
}
\]

則\((1)\)和\((2)\)就可以變為

\[{\max_w wS_bw\\\min_w wS_ww}
\]

LDA中通過二者相比，把它們統一成了一個優化問題：

\[\max_{w}\frac{wS_bw}{wS_ww}\tag{3}
\]

\((3)\)中的目標函數是一個瑞利商（Rayleigh Quotient）（以後會有更多涉及到它的演算法）的形式，這裡我們先假定\(S_w\)是非奇異的（\(S_w\)是奇異的情況以後會專門討論），這類優化問題的一般解法是變為以下形式

\[\max_{wS_ww=1}\frac{wS_bw}{wS_ww}=\max_{wS_ww=1}wS_bw\tag{4}
\]

這個變換是合理的，假設\(w_0\)是\((3)\)中最優的投影向量，由於\(S_w\)非奇異（換句話說，\(S_w\)是正定的），則總存在一個正數\(k\)：

\[w_0^TS_ww_0=k>0
\]

那麼總存在一個\(w_*=w_0/\sqrt k\)，有

\[\frac{w_0S_bw_0}{w_0S_ww_0}=\frac{w_*S_bw_*}{w_*S_ww_*},\quad w_*S_ww_*=\frac{w_0S_ww_0}{k}=1
\]

這就說明存在一個\(w_*\)，使得

\[w_*^TS_ww_*=1,\quad w_*=\arg\max_w\frac{wS_bw}{wS_ww}
\]

也就是說\(w\)的長度不對\((3)\)的求解產生任何影響，因此顯然\((3)\)和\((4)\)在這種情況下是等價的。根據\((4)\)，使用拉格朗日乘數法得到：

\[S_bw=\lambda S_ww
\]

這是一個廣義特徵方程，由於\(S_w\)正定，所以\(w\)實際上就是\(S_w^{-1}S_b\)最大特徵值對應的特徵向量。

我們得到了\(w\)，就可以將樣本投影到一個子空間中，即\(X’=w^TX\)，對於訓練樣本以外的未知數據\(x\)，如何辨認它屬於哪個類呢？首先把它投影到子空間中：

\[x’=w^Tx
\]

然後採用K近鄰演算法（K-Nearest Neighbor, KNN），即找到離\(x’_w\)最近的\(k\)個訓練樣本（歐式距離），然後統計這\(k\)個樣本都是哪個類的，不妨設這些樣本的類編號為\(L=[l_1,l_2,\cdots,l_k]\)，最後選擇\(L\)中的眾數作為\(x’\)的分類結果。

KNN是一個十分簡易且常用的分類演算法，往往取\(k=1,3,5\)進行分類。由於計算高維數據的歐式距離十分耗時，因此KNN常與降維演算法配合使用。當然，不只是在使用LDA時才可以使用KNN，PCA以及其它降維演算法也可以配合KNN對未知樣本進行分類，但PCA的分類效果一般沒有LDA好（因為PCA是無監督的）。

2. 多個投影的LDA

現在我們要求的是一個投影矩陣\(W\in\mathbb R^{m\times d}\)，優化問題中的類間、類內散度矩陣沒有變，優化問題\((3)\)變為：

\[\max_{w}\frac{tr(W^TS_bW)}{tr(W^TS_wW)}\tag{5}
\]

同樣當\(S_w\)是非奇異的時候，我們令\(W^TS_wW=I\)，類似的就可以得到，\(W\)即為\(S_w^{-1}S_b\)最大的\(d\)個特徵值對應的特徵向量組成。在這裡我們需要注意，類間散度矩陣的秩總是不大於\(c-1\)，即：

\[\mathrm{rank}(S_b)\leq c-1
\]

所以\(S_w^{-1}S_b\)的非零特徵值也最多只有\(c-1\)個，也就是說投影向量的個數\(d\)最多只能有\(c-1\)個，即

\[d\leq c-1
\]

因為之後得到的投影向量都將在\(S_b\)的零空間中，假設這個投影向量是\(w’\)，則\(S_bw’=0\)，對優化沒有產生任何幫助，所以這些向量應當捨棄。也就是說LDA中，我們最多只能獲取到\(c-1\)個有效的投影。

總結一下，LDA的步驟為：

計算類間、類內散度矩陣\(S_b,S_w\)
計算\(S_b^{-1}S_w\)的特徵分解，取前\(d\ (\leq c-1)\)個最大特徵值對應的特徵向量作為投影矩陣\(W\)
對訓練樣本投影\(X’=W^TX\)，對於未知樣本\(x\)也投影：\(x’=W^Tx\)，然後使用KNN進行分類。

Tags: 機器學習-降維篇