面試必備：高頻演算法題匯總「圖文解析 + 教學影片 + 範例程式碼」之 字元串處理+動態規劃 合集！

• 2019 年 10 月 19 日
• 筆記

Attention

秋招接近尾聲，我總結了 牛客、WanAndroid 上，有關筆試面經的帖子中出現的演算法題，結合往年考題寫了這一系列文章，所有文章均與 LeetCode 進行核對、測試。歡迎食用

本文將覆蓋 「字元串處理」 + 「動態規劃」 方面的面試演算法題，文中我將給出：

1. 面試中的題目
2. 解題的思路
3. 特定問題的技巧和注意事項
4. 考察的知識點及其概念
5. 詳細的程式碼和解析

開始之前，我們先看下會有哪些重點案例：

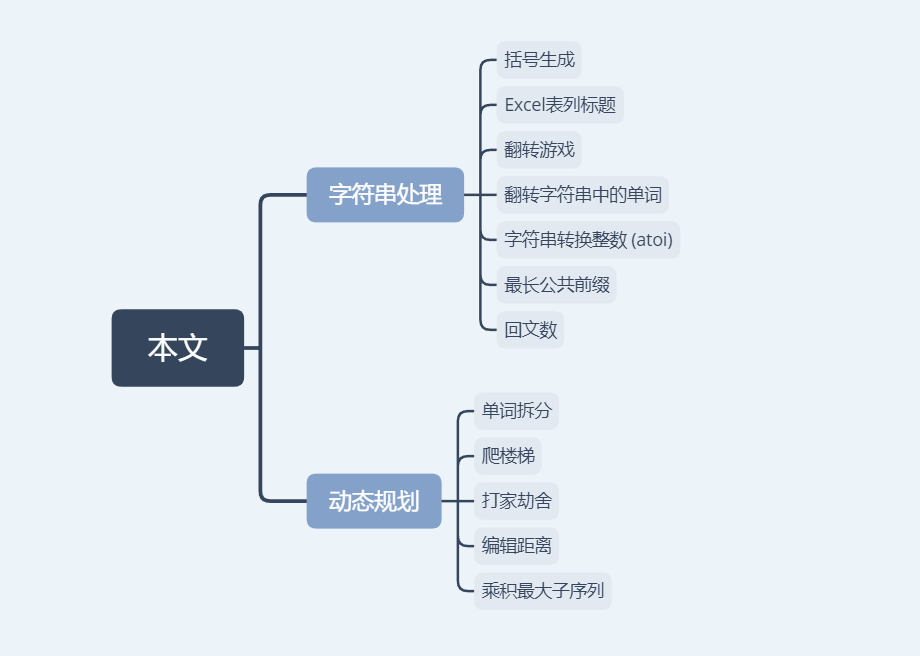
為了方便大家跟進學習，我在 GitHub 建立了一個倉庫

倉庫地址：超級乾貨！精心歸納影片、歸類、總結，各位路過的老鐵支援一下！給個 Star ！

現在就讓我們開始吧！

字元串處理

字元串廣泛應用 在 Java 編程中，在 Java 中字元串屬於對象，Java 提供了 String 類來創建和操作字元串。面試中的字元串處理問題，主要是對於字元串各種方法的靈活應用。下面結合實例，講講常見的考點：

括弧生成

給定 n，表示有 n 對括弧, 請寫一個函數以將其生成所有的括弧組合，並返回組合結果。

例如

給出 n = 3，生成結果為：    [    "((()))",    "(()())",    "(())()",    "()(())",    "()()()"  ]

解題思路

使用 回溯法

只有在我們知道序列仍然保持有效時才添加 ‘(‘ or ‘)’，而不是像 方法一 那樣每次添加。我們可以通過跟蹤到目前為止放置的左括弧和右括弧的數目來做到這一點，

如果我們還剩一個位置，我們可以開始放一個左括弧。 如果它不超過左括弧的數量，我們可以放一個右括弧。

影片

影片講解和源碼-生成括弧

public List<String> generateParenthesis(int n) {      List<String> res = new ArrayList<>();      helper(n, n, "", res);      return res;  }    // DFS  private void helper(int nL, int nR, String parenthesis, List<String> res) {      // nL 和 nR 分別代表左右括弧剩餘的數量      if (nL < 0 || nR < 0) {          return;      }        if (nL == 0 && nR == 0) {          res.add(parenthesis);          return;      }      helper(nL - 1, nR, parenthesis + "(", res);      if (nL >= nR) {          return;      }      helper(nL, nR - 1, parenthesis + ")", res);  }

複雜度

Excel表列標題

給定一個正整數，返回相應的列標題，如Excel表中所示。如:
1 -> A，
2 -> B
…
26 -> Z，
27 -> AA

示例 :

輸入: 28  輸出: "AB"

解題思路

• 網上看了 n 多人的方法，感覺很多都做麻煩了。大多數人都困在這個 『A』 或者說 n = 0 上
• 舉個例子，如果輸入 26，我們一般會直接把它 %26 這樣得到的就是一個 0
• 然而很多人得到字元的方式都是 %26 + 64，也就是 0 + 『A』 = ‘A’ ,正確答案當然是 『Z』，於是加了一堆判斷
• 其實不用那麼麻煩，一個 n– 就能搞定.

public String convertToTitle (int n) {      StringBuilder str = new StringBuilder();        while (n > 0) {          n--;          str.append ( (char) ( (n % 26) + 'A'));          n /= 26;      }      return str.reverse().toString();  }

翻轉遊戲

給定一個只包含兩種字元的字元串：+和-，你和你的小夥伴輪流翻轉"++"變成"–"。當一個人無法採取行動時遊戲結束，另一個人將是贏家。編寫一個函數，計算字元串在一次有效移動後的所有可能狀態。

示例 :

輸入：s = "++++"  [    "--++",    "+--+",    "++--"  ]

解題思路

1. 我們從第二個字母開始遍歷
2. 每次判斷當前字母是否為+，和之前那個字母是否為+
3. 如果都為加，則將翻轉後的字元串存入結果中即可

public List<String> generatePossibleNextMoves (String s) {      List list = new ArrayList();      // indexOf 方法使用 看下方拓展      for (int i = -1; (i = s.indexOf ("++", i + 1)) >= 0;) {          list.add (s.substring (0, i) + "--" + s.substring (i + 2));      }      return list;  }

拓展：

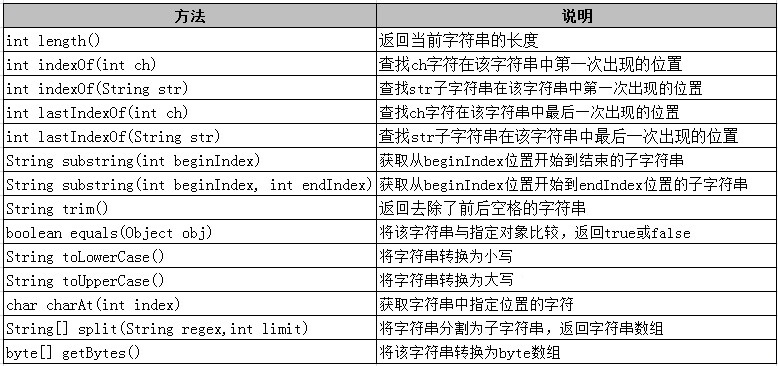
Java中字元串中子串的查找共有四種方法，如下：

1. int indexOf(String str) ：返回第一次出現的指定子字元串在此字元串中的索引。
2. int indexOf(String str, int startIndex)：從指定的索引處開始，返回第一次出現的指定子字元串在此字元串中的索引。
3. int lastIndexOf(String str) ：返回在此字元串中最右邊出現的指定子字元串的索引。
4. int lastIndexOf(String str, int startIndex) ：從指定的索引處開始向後搜索，返回在此字元串中最後一次出現的指定子字元串的索引。

substring() 方法返回字元串的子字元串。

1. public String substring(int beginIndex) 返回 beginIndex 後的字元串
2. public String substring(int beginIndex, int endIndex) 返回 beginIndex 到 endIndex 之間的字元串

翻轉字元串中的單詞

給定一個字元串，逐個翻轉字元串中的每個單詞。

示例 ：

輸入: "a good   example"  輸出: "example good a"  解釋: 如果兩個單詞間有多餘的空格，將反轉後單詞間的空格減少到只含一個。

解題思路

1. 通過 split 方法，以 「 」 為標識符為基準拆分字元串
2. 將拆分後的字元串倒序插入數組中即可

public String reverseWords(String s) {      if(s.length() == 0 || s == null){          return " ";      }      //按照空格將s切分      String[] array = s.split(" ");      StringBuilder sb = new StringBuilder();      //從後往前遍歷array，在sb中插入單詞      for(int i = array.length - 1; i >= 0; i--){          if(!array[i].equals("")) {              // 為防止字元串首多一個 「 」 判斷當前是不是空字元串              // 是字元串第一個就不輸出空格              if (sb.length() > 0) {                  sb.append(" ");              }                sb.append(array[i]);          }      }      return sb.toString();  }

字元串轉換整數 (atoi)

實現atoi這個函數，將一個字元串轉換為整數。如果沒有合法的整數，返回0。如果整數超出了32位整數的範圍，返回 INT_MAX(2147483647) 如果是正整數，或者 INT_MIN(-2147483648) 如果是負整數。

示例 :

輸入: "4193 with words"  輸出: 4193  解釋: 轉換截止於數字 '3' ，因為它的下一個字元不為數字。  示例 4:    輸入: "words and 987"  輸出: 0  解釋: 第一個非空字元是 'w', 但它不是數字或正、負號。       因此無法執行有效的轉換。

解題思路

1. 首先我們要知道該數正負
2. 根據題意調用 trim() 去掉空格
3. 去完多餘空格之後，首位有三種情況 『+』 『-』 其他
4. 設一個 falg 叫做 sign 默認值為一，如果監測到 『-』 則設為 -1
5. 這樣一來後面求出的結果乘以 sigh 就能帶上正負值
6. 在定義一個 num 值用於保存答案數值
7. for 循環從頭到尾訪問字元串
8. 先判斷當前位是否為數字，這時分兩種情況
9. 如果字元串首位就不是數字和 -+ 號，根據題意直接退出循環
10. 如果為數字就將 sum 的值 *10 倍，再將其加入 sum 中
11. 如果值超過 MAX_VALUE 跳出循環
12. 對應 *sigh 輸出正負值，或者 MAX_VALUE 或 MIN_VALUE 即可

影片

影片講解和源碼-字元串轉換整數

public int myAtoi(String str) {      if(str == null) {          return 0;      }      str = str.trim();      if (str.length() == 0) {          return 0;      }        int sign = 1;      int index = 0;        if (str.charAt(index) == '+') {          index++;      } else if (str.charAt(index) == '-') {          sign = -1;          index++;      }      long num = 0;      for (; index < str.length(); index++) {          if (str.charAt(index) < '0' || str.charAt(index) > '9') {              break;          }          num = num * 10 + (str.charAt(index) - '0');          if (num > Integer.MAX_VALUE ) {              break;          }      }      if (num * sign >= Integer.MAX_VALUE) {          return Integer.MAX_VALUE;      }      if (num * sign <= Integer.MIN_VALUE) {          return Integer.MIN_VALUE;      }      return (int)num * sign;  }

註：trim() 函數是去掉String字元串的首尾空格;

最長公共前綴

編寫一個函數來查找字元串數組中的最長公共前綴。

如果不存在公共前綴，返回空字元串 ""。

示例 :

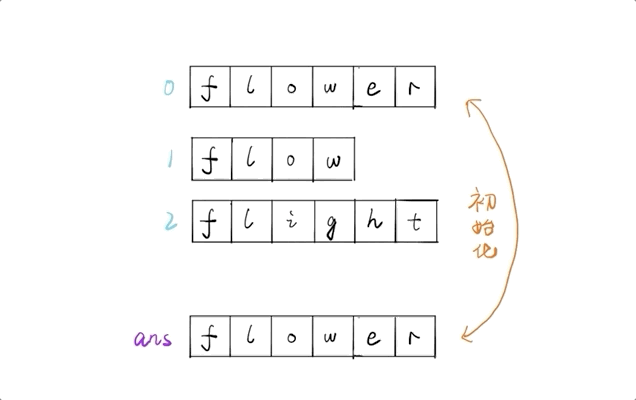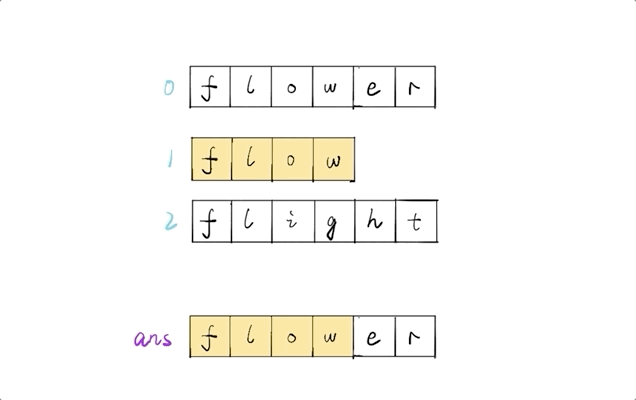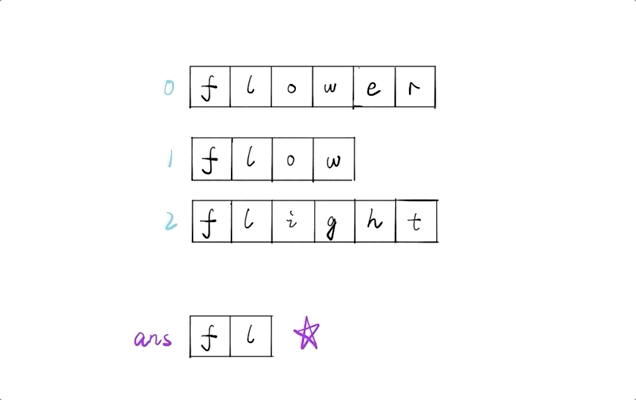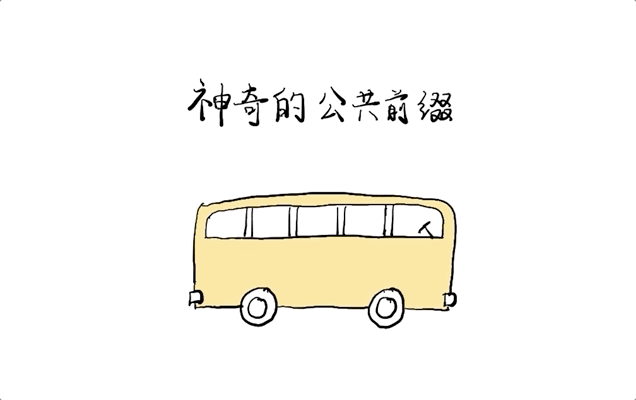
輸入: ["flower","flow","flight"]  輸出: "fl"

解題思路

標籤：鏈表
當字元串數組長度為 0 時則公共前綴為空，直接返回
令最長公共前綴 ans 的值為第一個字元串，進行初始化
遍歷後面的字元串，依次將其與 ans 進行比較，兩兩找出公共前綴，最終結果即為最長公共前綴
如果查找過程中出現了 ans 為空的情況，則公共前綴不存在直接返回
s 為所有字元串的長度之和

影片

最長公共前綴

public String longestCommonPrefix(String[] strs) {      if (strs == null || strs.length == 0) {          return "";      }      String prefix = strs[0];      for(int i = 1; i < strs.length; i++) {          int j = 0;          while (j < strs[i].length() && j < prefix.length() && strs[i].charAt(j) == prefix.charAt(j)) {              j++;          }          if( j == 0) {              return "";          }          prefix = prefix.substring(0, j);      }      return prefix;  }

時間複雜度：

(O(s))

迴文數

判斷一個正整數是不是迴文數。迴文數的定義是，將這個數反轉之後，得到的數仍然是同一個數。

示例 :

輸入: 121  輸出: true

解題思路

通過取整和取余操作獲取整數中對應的數字進行比較。

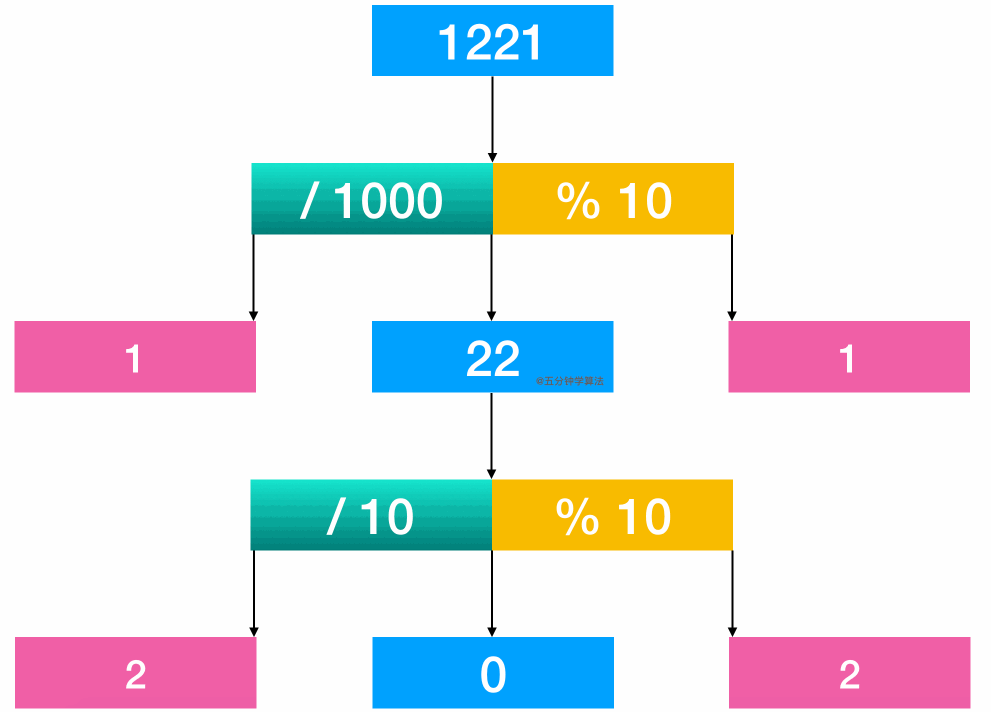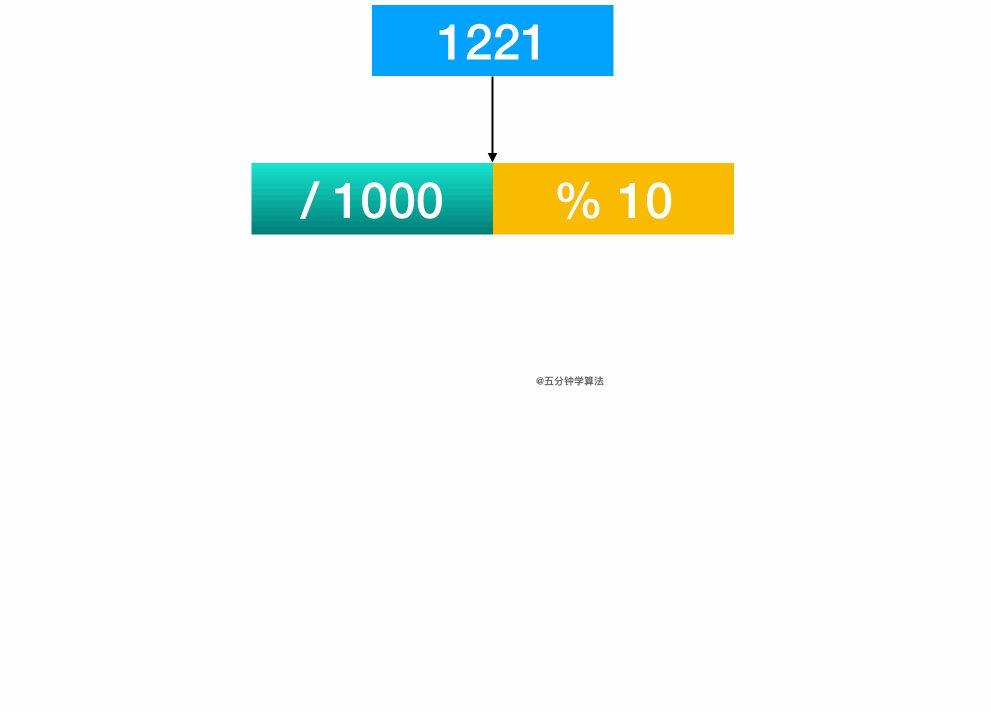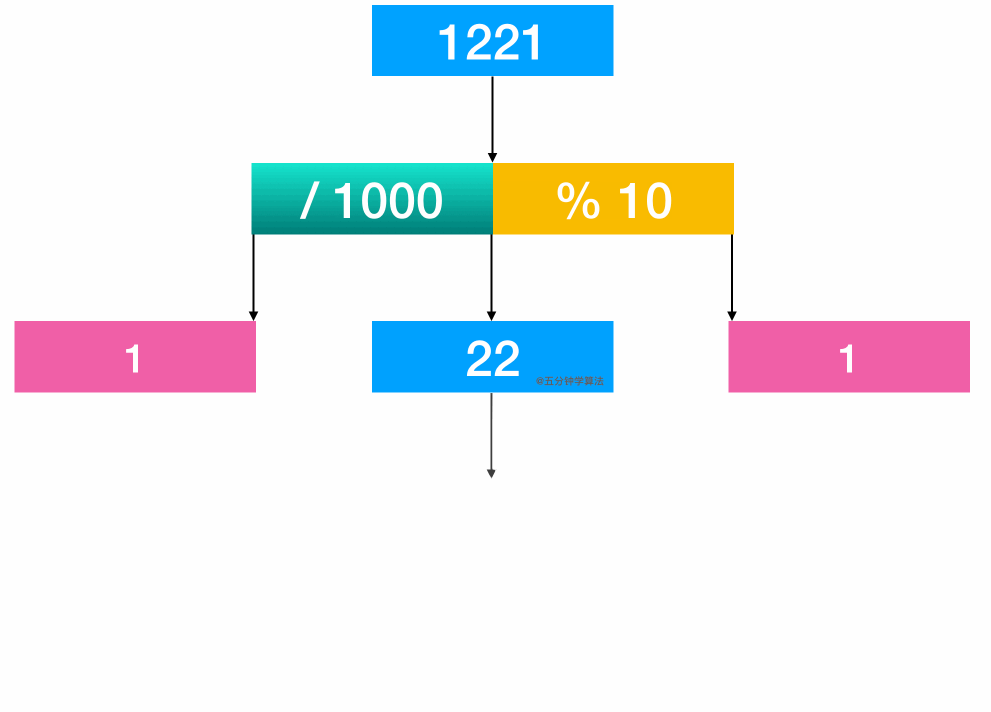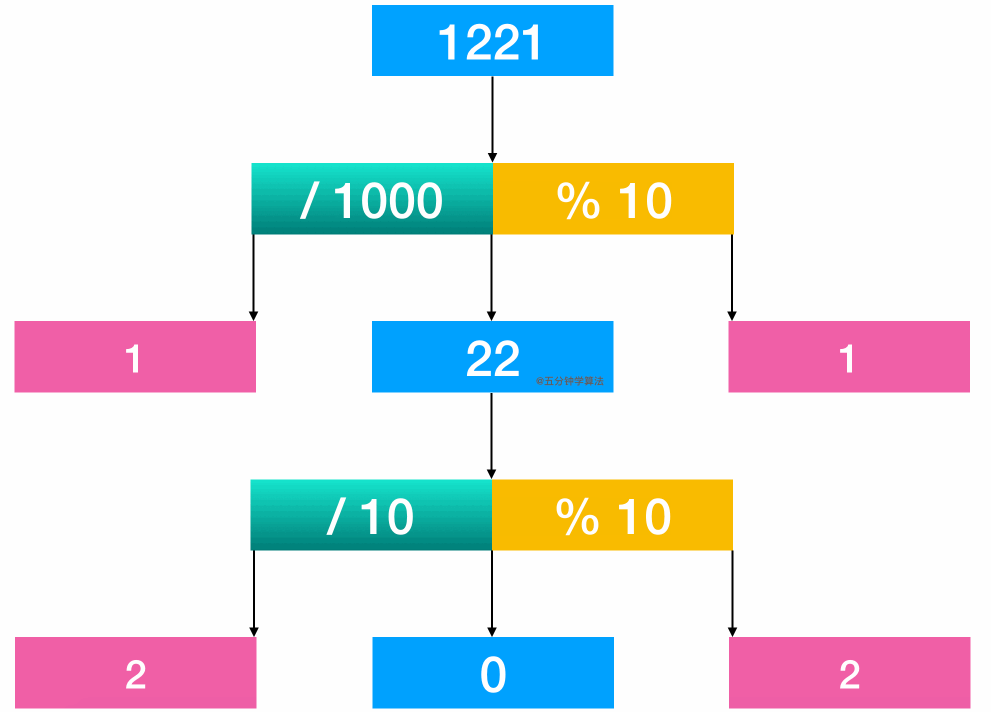
舉個例子：1221 這個數字。

通過計算 1221 / 1000， 得首位1
通過計算 1221 % 10， 可得末位 1
進行比較
再將 22 取出來繼續比較

影片

迴文數

public boolean palindromeNumber(int num) {      // Write your code here      if(num < 0){          return false;      }      int div = 1;      while(num / div >= 10){          div *= 10;      }      while(num > 0){          if(num / div != num % 10){              return false;          }          num = (num % div) / 10;          div /= 100;      }      return true;  }

動態規劃

動態規劃常常適用於有重疊子問題和最優子結構性質的問題，動態規劃方法所耗時間往往遠少於樸素解法。其背後的基本思想非常簡單。大致上，若要解一個給定問題，我們需要解其不同部分（即子問題），再根據子問題的解以得出原問題的解。

通常許多子問題非常相似，為此動態規劃法試圖僅僅解決每個子問題一次，從而減少計算量：一旦某個給定子問題的解已經算出，則將其記憶化存儲，以便下次需要同一個子問題解之時直接查表。這種做法在重複子問題的數目關於輸入的規模呈指數增長時特別有用。

單詞拆分

給定字元串 s 和單詞字典 dict，確定 s 是否可以分成一個或多個以空格分隔的子串，並且這些子串都在字典中存在。

示例 ：

輸入: s = "applepenapple", wordDict = ["apple", "pen"]  輸出: true  解釋: 返回 true 因為 "applepenapple" 可以被拆分成 "apple pen apple"。       注意你可以重複使用字典中的單詞。

解題思路

這個方法的想法是對於給定的字元串 s 可以被拆分成子問題 s1 和 s2 。如果這些子問題都可以獨立地被拆分成符合要求的子問題，那麼整個問題 s 也可以滿足。也就是，如果 (catsanddog) 可以拆分成兩個子字元串 "(catsand)" 和 "(dog)" 。子問題 "(catsand)" 可以進一步拆分成 "(cats)" 和 "(and)" ，這兩個獨立的部分都是字典的一部分，所以 "(catsand)" 滿足題意條件，再往前， "(catsand)" 和 "(dog)" 也分別滿足條件，所以整個字元串 "(catsanddog)" 也滿足條件。

現在，我們考慮 (dp) 數組求解的過程:

1. 我們使用 (n+1) 大小數組的 (dp) ，其中 (n) 是給定字元串的長度。
2. 我們也使用 2 個下標指針 (i) 和 (j) ，其中 (i) 是當前字元串從頭開始的子字元串(（s'）)的長度， (j) 是當前子字元串(（s'）)的拆分位置，拆分成 (s'(0,j))和 (s'(j+1,i))。
3. 為了求出 (dp) 數組，我們初始化 (dp[0]) 為 (true) ，這是因為空字元串總是字典的一部分。 (dp) 數組剩餘的元素都初始化為 (false) 。
4. 我們用下標 (i) 來考慮所有從當前字元串開始的可能的子字元串。對於每一個子字元串，我們通過下標 (j) 將它拆分成 s1' 和 s2'（注意 i 現在指向 s2' 的結尾）。
5. 為了將 (dp[i]) 數組求出來，我們依次檢查每個 (dp[j]) 是否為 (true) ，也就是子字元串 s1′ 是否滿足題目要求。如果滿足，我們接下來檢查 s2′ 是否在字典中。如果包含，我們接下來檢查 s2′ 是否在字典中，如果兩個字元串都滿足要求，我們讓 (dp[i]) 為 (true) ，否則令其為 (false) 。

    public boolean wordBreak(String s, List<String> wordDict) {          Set<String> wordDictSet=new HashSet(wordDict);          boolean[] dp = new boolean[s.length() + 1];          dp[0] = true;          for (int i = 1; i <= s.length(); i++) {              for (int j = 0; j < i; j++) {                  if (dp[j] && wordDictSet.contains(s.substring(j, i))) {                      dp[i] = true;                      break;                  }              }          }          return dp[s.length()];      }

複雜度分析

時間複雜度：(O(n^2)) 。求出 (dp) 數組需要兩重循環。

空間複雜度：(O(n))。(dp) 數組的長度是 (n+1)。

爬樓梯

假設你正在爬樓梯。需要 n 階你才能到達樓頂。

每次你可以爬 1 或 2 個台階。你有多少種不同的方法可以爬到樓頂呢？

注意：給定 n 是一個正整數。

示例 :

輸入： 3  輸出： 3  解釋： 有三種方法可以爬到樓頂。   1 階 + 1 階 + 1 階   1 階 + 2 階   2 階 + 1 階

解題思路

感覺這題類似斐波那契數列。不難發現，這個問題可以被分解為一些包含最優子結構的子問題，即它的最優解可以從其子問題的最優解來有效地構建，我們可以使用動態規劃來解決這一問題。

第 (i) 階可以由以下兩種方法得到：

在第 ((i−1)) 階後向上爬 1 階。

在第 ((i−2)) 階後向上爬 2 階。

所以到達第 (i) 階的方法總數就是到第 ((i−1)) 階和第 ((i−2)) 階的方法數之和。

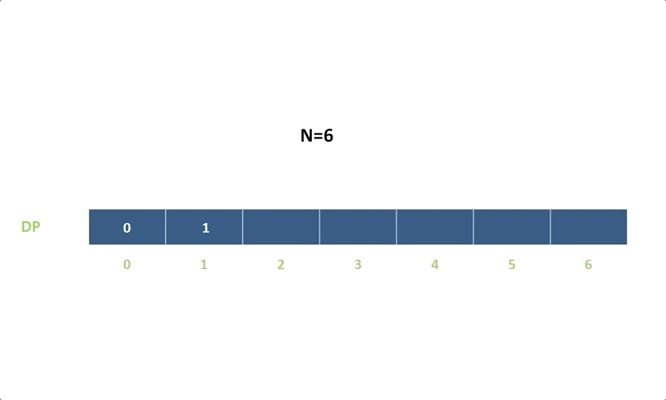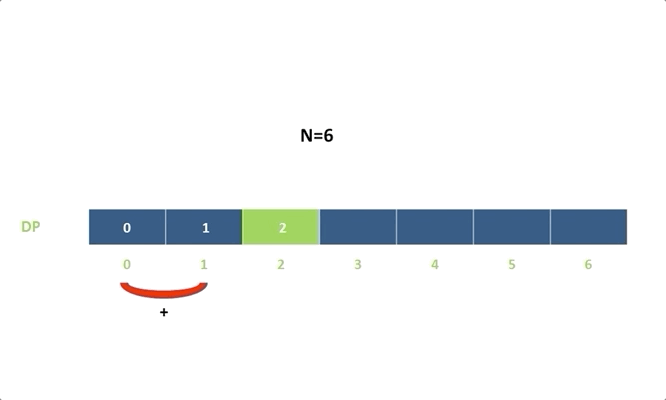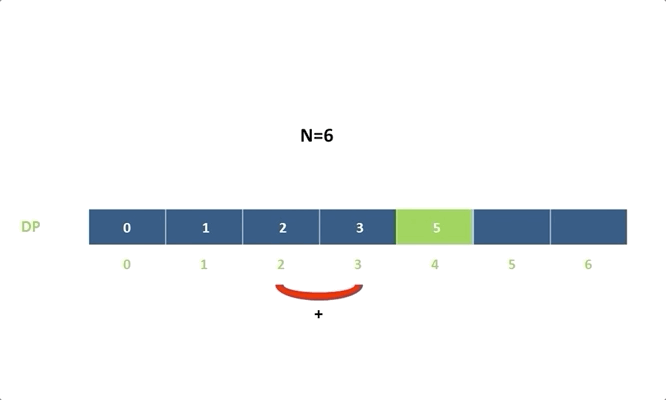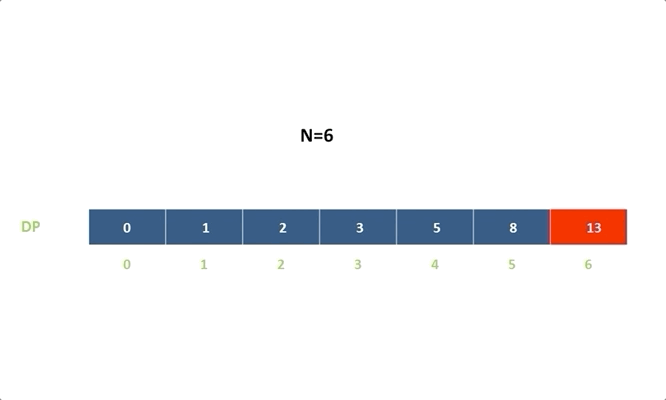
令 (dp[i]) 表示能到達第 (i) 階的方法總數：

(dp[i]=dp[i-1]+dp[i-2])
(dp[i]=dp[i−1]+dp[i−2])

public int climbStairs(int n) {      if (n == 0) return 0;      int[] array = new int[n + 1];      array[0] = 1;      if (array.length > 1) {          array[1] = 1;      }        for(int i = 2; i < array.length; i++) {          array[i] = array[i - 1] + array[i - 2];      }      return array[n];  }

打家劫舍

假設你是一個專業的竊賊，準備沿著一條街打劫房屋。每個房子都存放著特定金額的錢。你面臨的唯一約束條件是：相鄰的房子裝著相互聯繫的防盜系統，且 當相鄰的兩個房子同一天被打劫時，該系統會自動報警。給定一個非負整數列表，表示每個房子中存放的錢， 算一算，如果今晚去打劫，在不觸動報警裝置的情況下, 你最多可以得到多少錢 。

示例 :

輸入: [2,7,9,3,1]  輸出: 12  解釋: 偷竊 1 號房屋 (金額 = 2), 偷竊 3 號房屋 (金額 = 9)，接著偷竊 5 號房屋 (金額 = 1)。       偷竊到的最高金額 = 2 + 9 + 1 = 12 。

解題思路

考慮所有可能的搶劫方案過於困難。一個自然而然的想法是首先從最簡單的情況開始。記：

(f(k) =) 從前 k 個房屋中能搶劫到的最大數額，(A_i) = 第 i 個房屋的錢數。

首先看 n = 1 的情況，顯然 f(1) = (A_1) 。

再看 n = 2，(f(2) = max(A_1 , A_2 ))。

對於 n = 3，有兩個選項:

搶第三個房子，將數額與第一個房子相加。

不搶第三個房子，保持現有最大數額。

顯然，你想選擇數額更大的選項。於是，可以總結出公式：

(f(k) = max(f(k – 2) + A_k , f(k – 1)))

我們選擇 (f(–1) = f(0) = 0) 為初始情況，這將極大地簡化程式碼。

答案為 (f(n))。可以用一個數組來存儲並計算結果。不過由於每一步你只需要前兩個最大值，兩個變數就足夠用了。

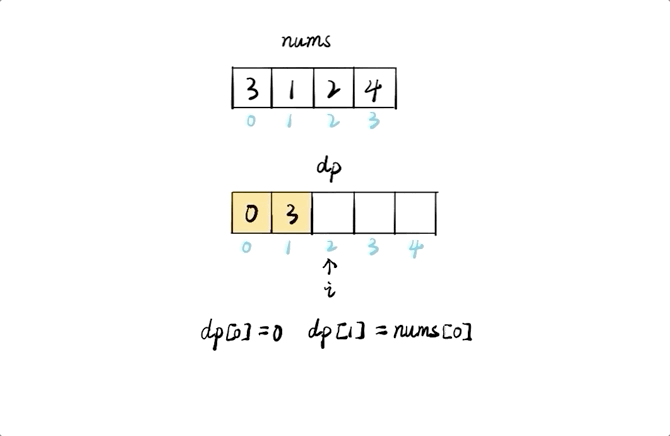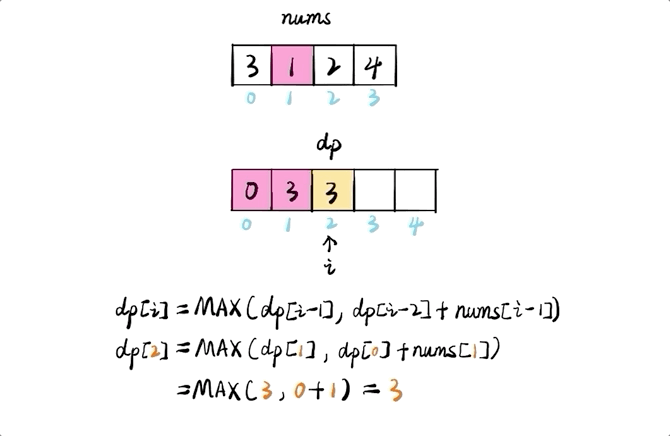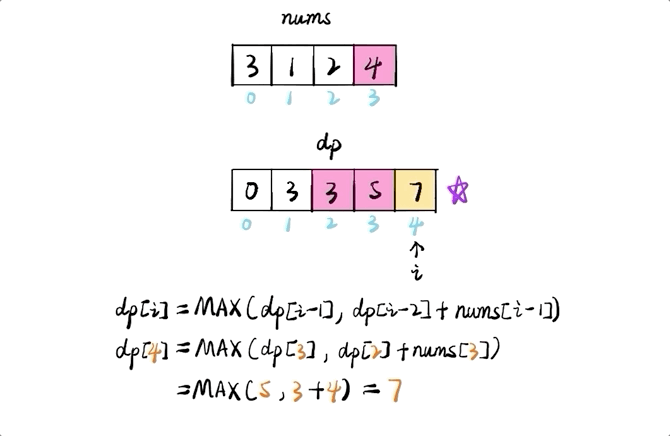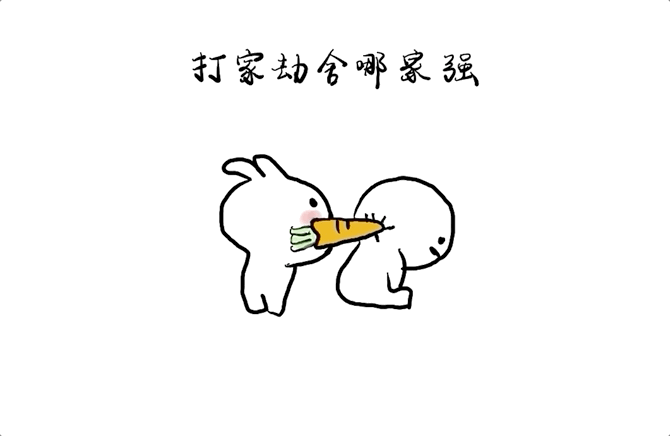
public long houseRobber(int[] A) {      if (A.length == 0) return 0;      long[] res = new long[A.length + 1];      res[0] = 0;      res[1] = A[0];      for (int i = 2; i < res.length; i++) {          res[i] = Math.max(res[i - 2] + A[i - 1], res[i - 1]);      }      return res[A.length];  }

複雜度分析

時間複雜度：(O(n))。其中 n 為房子的數量。
空間複雜度：(O(1))。

編輯距離

給出兩個單詞word1和word2，計算出將 word1 轉換為word2的最少操作次數。你總共三種操作方法：插入一個字元、刪除一個字元、替換一個字元。

示例 :

輸入: word1 = "horse", word2 = "ros"  輸出: 3  解釋:  horse -> rorse (將 'h' 替換為 'r')  rorse -> rose (刪除 'r')  rose -> ros (刪除 'e')      輸入: word1 = "intention", word2 = "execution"  輸出: 5  解釋:  intention -> inention (刪除 't')  inention -> enention (將 'i' 替換為 'e')  enention -> exention (將 'n' 替換為 'x')  exention -> exection (將 'n' 替換為 'c')  exection -> execution (插入 'u')

解題思路

我們的目的是讓問題簡單化，比如說兩個單詞 horse 和 ros 計算他們之間的編輯距離 D，容易發現，如果把單詞變短會讓這個問題變得簡單，很自然的想到用 D[n][m] 表示輸入單詞長度為 n 和 m 的編輯距離。

具體來說，D[i][j] 表示 word1 的前 i 個字母和 word2 的前 j 個字母之間的編輯距離。

當我們獲得 D[i-1][j]，D[i][j-1] 和 D[i-1][j-1] 的值之後就可以計算出 D[i][j]。

每次只可以往單個或者兩個字元串中插入一個字元

那麼遞推公式很顯然了

如果兩個子串的最後一個字母相同，word1[i] = word2[i] 的情況下：

(D[i][j] = 1 + min(D[i – 1][j], D[i][j – 1], D[i – 1][j – 1] – 1))
(D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]−1))

否則，word1[i] != word2[i] 我們將考慮替換最後一個字元使得他們相同：

(D[i][j] = 1 + min(D[i – 1][j], D[i][j – 1], D[i – 1][j – 1]))
(D[i][j]=1+min(D[i−1][j],D[i][j−1],D[i−1][j−1]))

所以每一步結果都將基於上一步的計算結果，示意如下：

同時，對於邊界情況，一個空串和一個非空串的編輯距離為 D[i][0] = i 和 D[0][j] = j。

綜上我們得到了演算法的全部流程。

溫馨提示，如果思維不好理解的話，把解題思路記清楚就行

public int minDistance(String word1, String word2) {      // write your code here      int n = word1.length();      int m = word2.length();      int[][] dp = new int[n + 1][m + 1];      for (int i = 0; i < n + 1; i++){          dp[i][0] = i;      }      for (int j = 0; j < m + 1; j++){          dp[0][j] = j;      }      for (int i = 1; i< n + 1; i++){          for (int j = 1; j < m + 1; j++){              if (word1.charAt(i - 1) == word2.charAt(j - 1)){                  dp[i][j] = dp[i - 1][j - 1];              } else {                  dp[i][j] = 1 + Math.min(dp[i - 1][j - 1], Math.min(dp[i][j - 1], dp[i - 1][j]));              }          }      }      return  dp[n][m];  }

複雜度分析

時間複雜度 ：(O(m n))，兩層循環顯而易見。
空間複雜度 ：(O(m n))，循環的每一步都要記錄結果。

乘積最大子序列

給定一個整數數組 nums ，找出一個序列中乘積最大的連續子序列（該序列至少包含一個數）。

示例 :

輸入: [-2,0,-1]  輸出: 0  解釋: 結果不能為 2, 因為 [-2,-1] 不是子數組。

解題思路

1. 遍曆數組時計算當前最大值，不斷更新
2. 令imax為當前最大值，則當前最大值為 imax = max(imax * nums[i], nums[i])
3. 由於存在負數，那麼會導致最大的變最小的，最小的變最大的。因此還需要維護當前最小值imin，imin = min(imin * nums[i], nums[i])
4. 當負數出現時則imax與imin進行交換再進行下一步計算

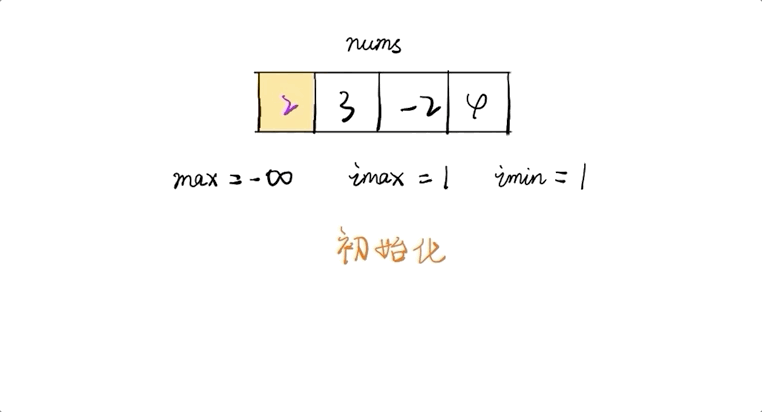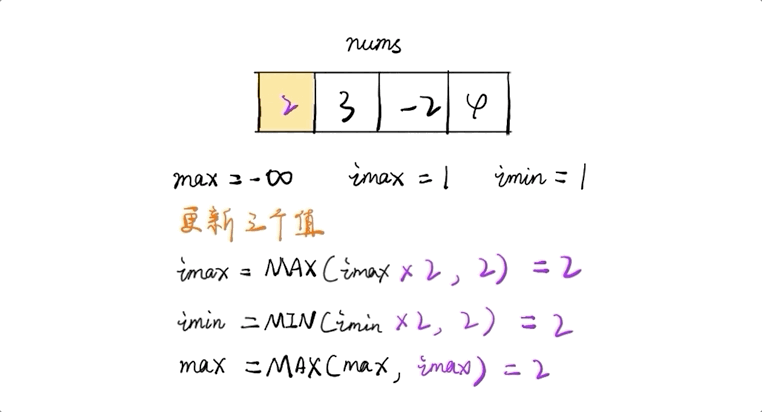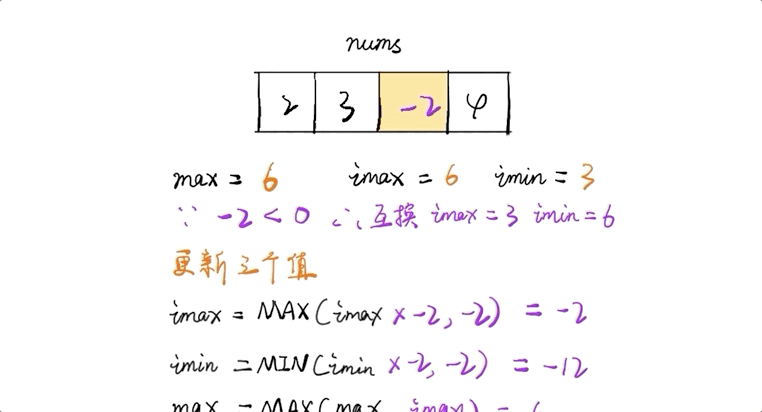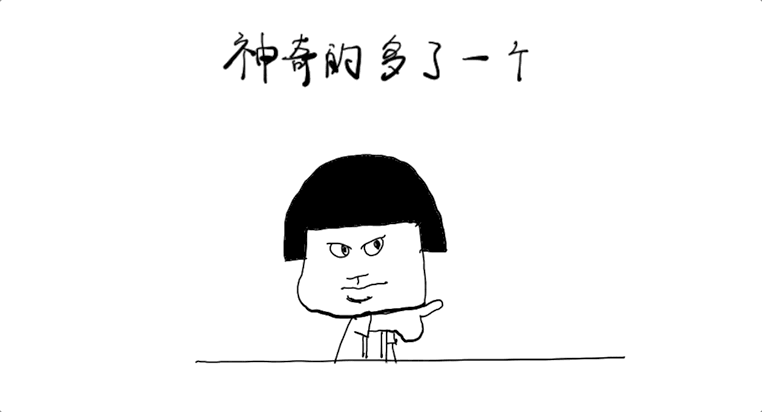
    public int maxProduct(int[] nums) {          int max = Integer.MIN_VALUE, imax = 1, imin = 1;          for(int i=0; i<nums.length; i++){              if(nums[i] < 0){                int tmp = imax;                imax = imin;                imin = tmp;              }              imax = Math.max(imax*nums[i], nums[i]);              imin = Math.min(imin*nums[i], nums[i]);                max = Math.max(max, imax);          }          return max;      }

時間複雜度：

• O(n)

Attention

• 為了提高文章品質，防止冗長乏味

下一部分演算法題

• 本片文章篇幅總結越長。我一直覺得，一片過長的文章，就像一堂超長的 會議/課堂，體驗很不好，所以我打算再開一篇文章

• 在後續文章中，我將繼續針對鏈表 棧 隊列 堆 動態規劃 矩陣 位運算 等近百種，面試高頻演算法題，及其圖文解析 + 教學影片 + 範例程式碼，進行深入剖析有興趣可以繼續關注 _yuanhao 的編程世界

• 不求快，只求優質，每篇文章將以 2 ～ 3 天的周期進行更新，力求保持高品質輸出

# 相關文章

「面試原題 + 圖文詳解 + 實例程式碼」二叉搜索樹-雙指針-貪心 面試題匯總
面試高頻演算法題匯總「圖文解析 + 教學影片 + 範例程式碼」之 二分 + 哈希表 + 堆 + 優先隊列 合集
?面試必備：高頻演算法題匯總「圖文解析 + 教學影片 + 範例程式碼」必知必會 排序 + 二叉樹 部分！?
每個人都要學的圖片壓縮終極奧義，有效解決 Android 程式 OOM
Android 讓你的 Room 搭上 RxJava 的順風車 從重複的程式碼中解脫出來
ViewModel 和 ViewModelProvider.Factory：ViewModel 的創建者
單例模式-全局可用的 context 對象，這一篇就夠了
縮放手勢 ScaleGestureDetector 源碼解析，這一篇就夠了
Android 屬性動畫框架 ObjectAnimator、ValueAnimator ，這一篇就夠了
看完這篇再不會 View 的動畫框架，我跪搓衣板

請點贊！因為你的鼓勵是我寫作的最大動力！

為了方便大家跟進學習，我在 GitHub 建立了一個倉庫

倉庫地址：超級乾貨！精心歸納影片、歸類、總結，各位路過的老鐵支援一下！給個 Star ！