點集配准技術（ICP、RPM、KC、CPD）
- 2019 年 10 月 16 日
- 筆記
在電腦視覺和模式識別中，點集配准技術是查找將兩個點集對齊的空間變換過程。尋找這種變換的目的主要包括：1、將多個數據集合併為一個全局統一的模型；2、將未知的數據集映射到已知的數據集上以識別其特徵或估計其姿態。點集的獲取可以是來自於3D掃描儀或測距儀的原始數據，在影像處理和影像配准中，點集也可以是通過從影像中提取獲得的一組特徵（例如角點檢測）。
點集配准研究的問題可以概括如下：假設{M，S}是空間Rd中的兩個點集，我們要尋找一種變換T，或者說是一種從Rd 空間到Rd 空間的映射，將其作用於點集M後，可以使得變換後的點集M和點集S之間的差異最小。將變換後的點集M記為T(M)，那麼轉換後的點集T(M)與點集S的差異可以由某種距離函數來定義，一種最簡單的方法是對配對點集取歐式距離的平方：
點集配准方法一般分為剛性配准和非剛性配准。
剛性配准：給定兩個點集，剛性配准產生一個剛性變換，該變換將一個點集映射到另一個點集。剛性變換定義為不改變任何兩點之間距離的變換，一般這種轉換隻包括平移和旋轉。
非剛性配准：給定兩個點集，非剛性配准產生一個非剛性變換，該變換將一個點集映射到另一個點集。非剛性變換包括仿射變換，例如縮放和剪切等，也可以涉及其他非線性變換。
下面我們來具體介紹幾種點集配准技術。
一. Iterative closest point（ICP）
ICP演算法是一種迭代方式的剛性配准演算法，它為點集M中每個點mi尋找在點集S中的最近點sj，然後利用最小二乘方式得到變換T，演算法偽程式碼如下：
ICP演算法對於待配對點集的初始位置比較敏感，當點集M的初始位置與點集S比較接近時，配准效果會比較好。另外ICP演算法在每次計算迭代過程中都會改變最近點對，所以其實很難證明ICP演算法能準確收斂到局部最優值，但是由於ICP演算法直觀易懂且易於實現，因此它目前仍然是最常用的點集配准演算法。
在計算變換T時可以使用SVD方式，過程如下：
優化目標：
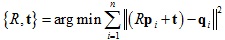
1.將點集去中心化：
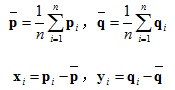
2.計算協方差矩陣並SVD分解：
3.計算旋轉矩陣和平移向量：
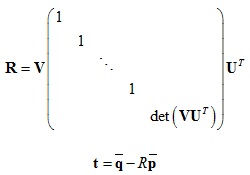
二. Robust point matching（RPM）
RPM演算法是一種使用退火和軟對應方式的配准演算法。ICP演算法在迭代計算時利用距離最近原則來產生待配準點對，而RPM演算法利用軟對應方式為任意點對賦予0到1之間的值，並最終收斂到0或1，如果是1則代表這兩個點是配準點對。RPM演算法最終計算得到的配準點對是一一映射的，而ICP演算法通常不是。
RPM演算法定義配準的損失函數如下：
其中：
t是平移向量。
A是變換矩陣，如果是2D情況，矩陣A可以分解成4個變數{a，θ，b，c}，分別代表縮放係數，旋轉角度，垂直和水平剪切量。
g(A)代表變換矩陣的正則項，其作用是防止變換矩陣中出現較大值。
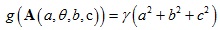
μ是配准矩陣，定義如下：
α項作用是是配准矩陣中有更多的配準點對數量
演算法偽程式碼如下：
三. Kernel correlation（KC）
KC演算法是一種相似性測量方法，它將點集配准問題轉化為尋找待配準點集之間最大相關性的過程。對於兩個點xi和xj，它們之間的核相關性（kernel correlation）定義為：
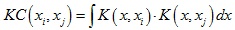
其中K(x, xi)是中心位置為xi的核函數，核函數通常為非負對稱函數，常用的核函數有高斯核函數等。
高斯核函數形式如下：
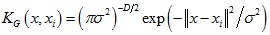
由高斯核函數可以得到的核相關性如下：
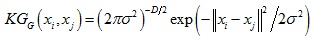
可以看到核相關性是與距離||xi – xj||相關的函數，值得注意的是，由其他核函數得到的核相關性也是距離||xi – xj||的函數。
KC演算法定義點集配準的損失函數如下：
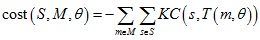
定義核密度估計（kernel density estimates）：
損失函數可以表示為兩個核密度估計之間的相關性：
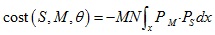
四. Coherent point drift（CPD）
CPD演算法將點集配准問題轉換為概率密度估計問題，其將點集M的分布表示成混合高斯模型，當點集M與點集S完成配准後，對應的似然函數達到最大。
將點集M中每個點mi作為混合高斯模型中每個成分的中心，並且假設每個成分概率相等，那麼其分布模型可以表示為：
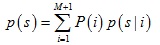
其中：
考慮雜訊的影響，在分布模型中又加入了均勻分布函數，其權重為w，這樣上式分布模型可以進一步表示為：
混合高斯模型的中心在配准過程中與變換參數θ相關，為了求得模型參數，需要極小化負對數似然函數：
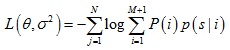
求解θ和σ2過程可以使用期望最大演算法，演算法包含兩步：
E-Step：通過舊的分布模型參數計算後驗概率分布Pold(i|sj)
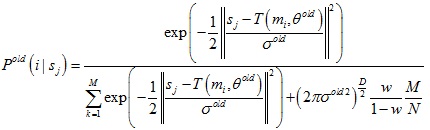
M-Step：極小化損失函數來得到新的模型參數θ和σ2
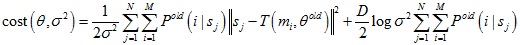
演算法偽程式碼如下：
在M-step中，對於剛性變換和非剛性變換，變換模型參數求解分別如下：
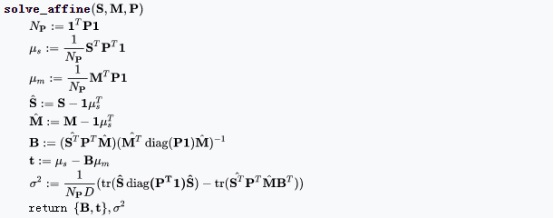
無異常點無雜訊情況
有異常點無雜訊情況
無異常點有雜訊情況
有異常點有雜訊情況
本文為原創，轉載請註明出處：http://www.cnblogs.com/shushen。
參考文獻：
[1] https://en.wikipedia.org/wiki/Point_set_registration
[2] https://igl.ethz.ch/projects/ARAP/svd_rot.pdf
[3] Gold S, Rangarajan A, Lu C, et al. New algorithms for 2D and 3D point matching : Pose estimation and correspondence. Pattern Recognition, 1998, 31(8): 1019-1031.
[4] Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding, 2003, 89(2): 114-141.
[5] Tsin Y, Kanade T. A Correlation-Based Approach to Robust Point Set Registration. european conference on computer vision, 2004: 558-569
[6] Myronenko A, Song X B. Point Set Registration: Coherent Point Drift. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(12): 2262-2275.
附錄
薄板樣條（Thin Plate Spline）
薄板樣條可以表示成徑向基函數的形式，給定一系列控制點{ci, i = 1, …, n}，徑向基函數定義了空間中從位置x到f(x)之間的映射關係：
薄板樣條對應的徑向基函數核為σ(r) = r2logr。
對於非剛性變換，如果使用薄板樣條來表示，那麼徑向基函數的自變數和應變數可以分別認為是變換前的點坐標x和變換後的點坐標y。
下面具體介紹如何使用薄板樣條表示非剛性變換。
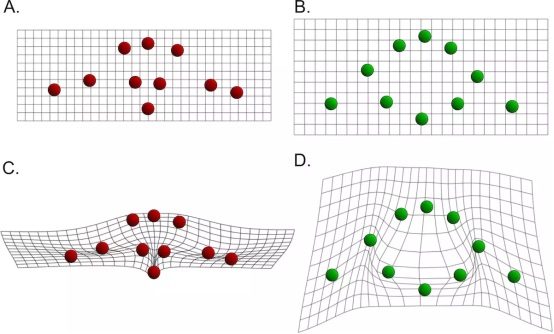
假設自變數是2維空間中的一系列點集x（A圖所示），應變數也是2維空間中的一系列點集y（B圖所示），我們對應變數的每個維度進行薄板樣條插值，插值函數形式如下：
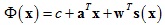
其中：c是標量，a ∈ R2×1，w ∈ Rn×1，s(x)表達式式如下：
插值函數表達式中c + aTx代表仿射變換，wTs(x)代表非仿射變換。
對於變換後每個點的第一個維度，我們可以建立一個約束條件：
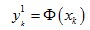
然後額外添加如下約束條件：
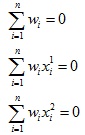
最終根據以上約束條件就可以求得薄板樣條插值函數的參數了。
期望最大演算法（Expectation Maximization）
期望最大演算法是解決含隱變數模型參數的一種方法。給定數據樣本X = {x(1), … , x(n)}，每個觀察樣本x(i)還對應著一個隱變數z(i)。假設樣本為獨立同分布，為了擬合模型p(x; θ)參數，我們需要極大化對數似然估計函數：
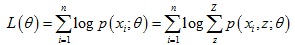
對於每個樣本x(i)，我們引入隱變數z的某種分布Qi(z)，那麼上式可以進一步變化：
上式最後一步利用了Jensen 不等式。
於是我們得到似然函數L(θ)的下界函數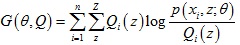
，那麼我們可以不斷最大化下界函數G(θ, Q)來使得L(θ)不斷提高，演算法過程如下：
1.（E-Step）固定θ，調整Q(z)，使得似然函數L(θ)與下界函數G(θ, Q)在θ處相等
2.（M-Step）固定Q(z)，調整θ，使得下界函數G(θ, Q)達到最大值。
3.迭代上述步驟，直至收斂到局部最優解。
對於第1步，只有當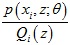
為常數時等號成立，又由於
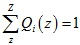，所以得到了Q(z)的表達式：
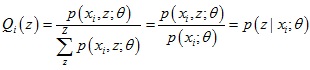
對於第2步，下界函數G(θ, Q)可以繼續推導，得到一個更簡單的表達形式：
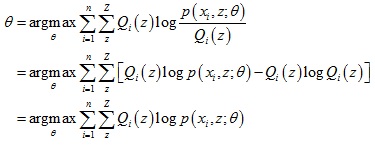
下面具體介紹以期望最大演算法來求解混合高斯模型的參數。
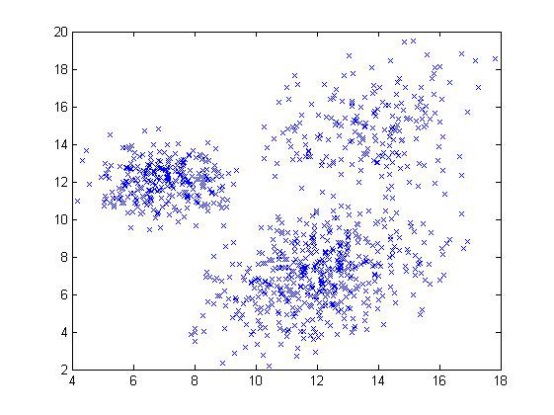
如上圖所示，給定一系列二維數據點x，假設這些數據是由3個正態分布函數隨機取樣得到，這些正態分布函數線性組合在一起就組成了混合高斯模型的概率密度函數：
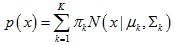
那麼得到對數似然估計函數如下：
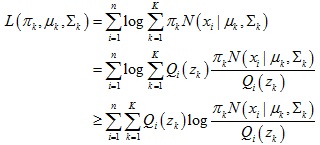
我們為每個數據點xi引入一個隱變數 z，這個隱變數代表這個數據點xi是由混合高斯模型中的哪個正態分布函數生成得到。
根據前面期望最大演算法步驟：
1.計算隱變數的分布Qi(zk)
Qi(zk)它代表了數據點xi是由第k個正態分布函數生成的概率：
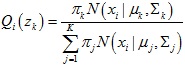
2.計算混合高斯模型參數πk，μk，Σk
下界函數進一步推導：
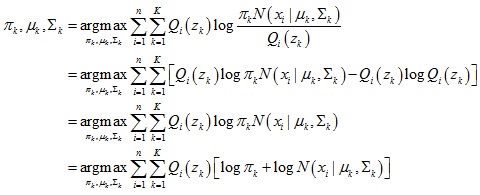
於是可以求出模型參數：
