[USACO3.1]形成的區域(掃描線+離散化)
[USACO3.1]形成的區域(P6432)
日期:2020-05-31
一、題意分析
- 任務:給出一張寬為\(A\)長為\(B\)的白紙(顏色為\(1\)),現要求將\(N\)個有顏色且不透明的長方形順序放在白紙上,可能重疊。求放好後那張紙上呈現的每種顏色的面積。
- 輸入:第一行三個正整數\(A \ B \ N\),分別表示白紙的長、白紙的寬、長方形的個數;第\(2\)到\(N+1\)行,每行五個整數\(llx \ lly \ urx \ ury \ color\),表示有一個左下角坐標為\((llx,lly)\)、右上角坐標為\((urx,ury)\)、顏色為\(color\)的長方形。
- 輸出:放好長方形後,輸出且只輸出那張紙上可視顏色的匯總。每行輸出兩個正整數,該可視顏色和其總可視面積。輸出時按照\(color\)升序輸出。
- 數據範圍(原題):\(1 \leq N \leq 10^3\),\(1 \leq A, B \leq 10^4\),\(1 \leq color \leq 2.5 \times 10^3\)。
二、演算法分析
1. 暴力
我們知道,暴力的時間複雜度為\(O(A·B·N)\),即\(10^{11}\),故無法\(AC\)。
所以,我們在\(Excel\)上枚舉暴力的過程,看看能否有所發現。
輸入樣例
20 20 3
2 2 18 18 2
0 8 19 19 3
8 0 10 19 4
0). 初始狀態(紅點為原點)
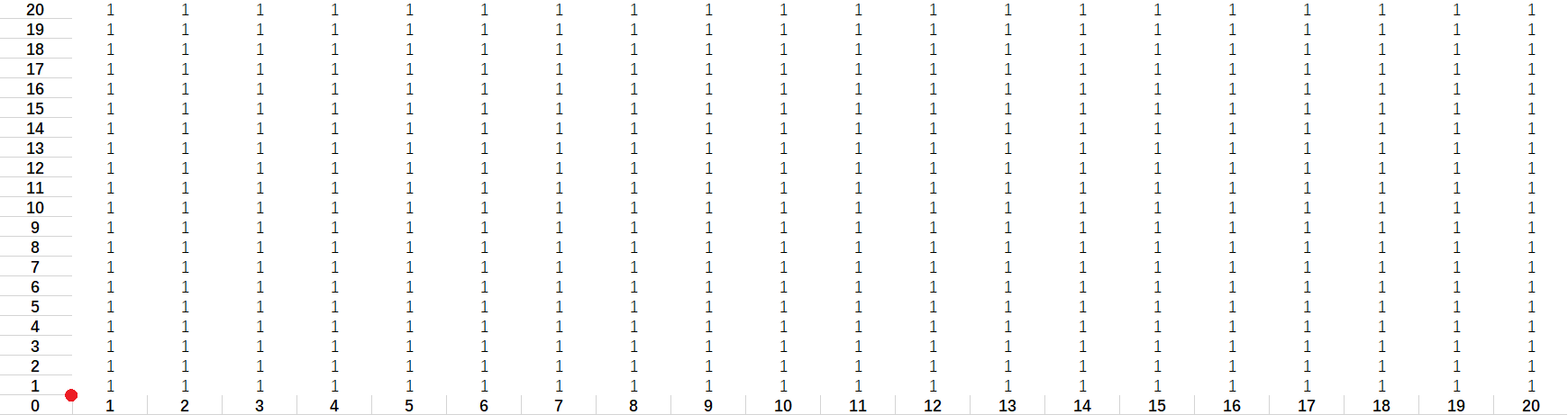
1). 放第一個長方形
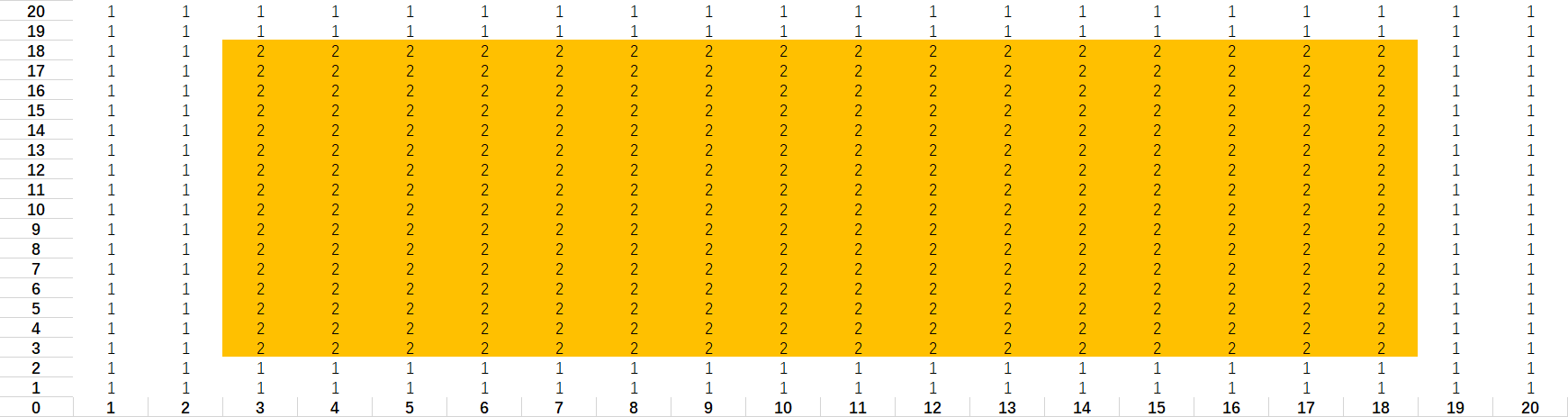
2). 放第二個長方形
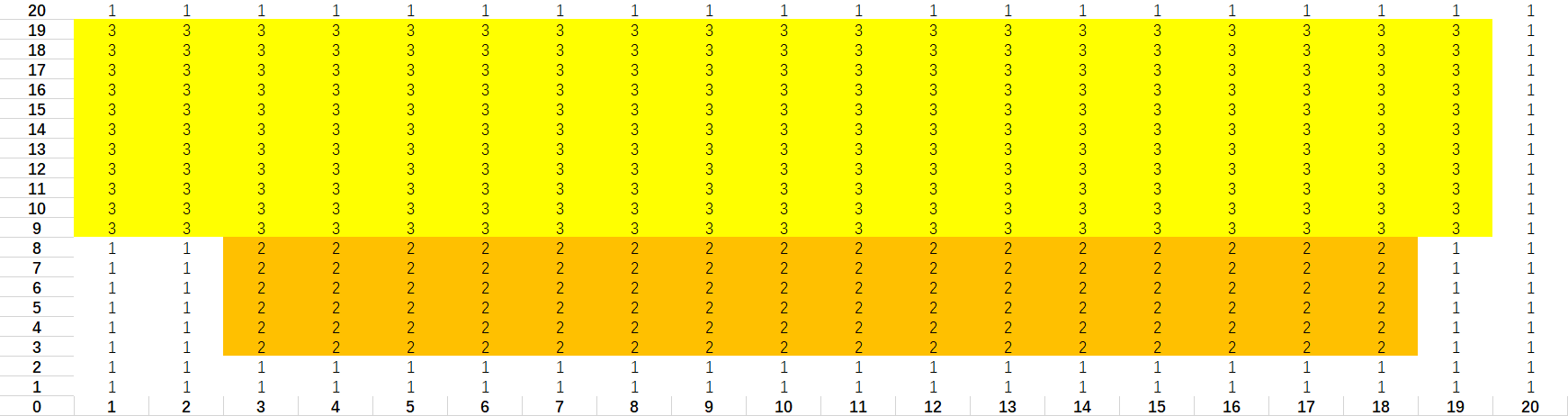
3). 放第三個長方形
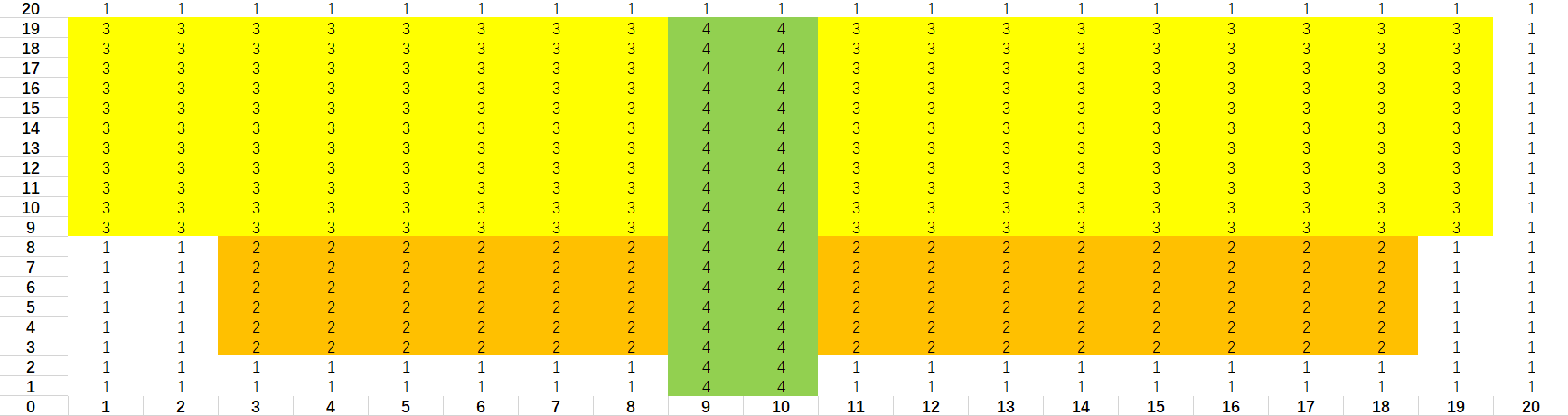
4). 驗證(用\(COUNTIF\)函數)
| 1 | 91 |
|---|---|
| 2 | 84 |
| 3 | 187 |
| 4 | 38 |
畫圖後,我們發現:其實填了大片相同的數字(顏色),如果我們只用一個數字來表示這個區域(小長方形)的話,那就會快很多。
2. 離散化
1). 掃描線
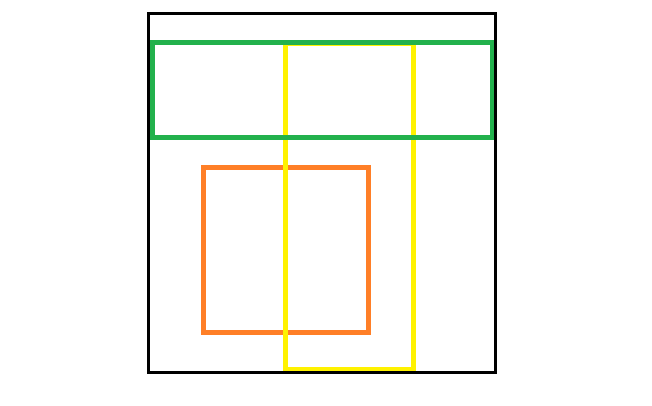
根據上面的想法,我們來繪製這三個長方形和黑色邊框的白紙的掃描線。掃描線就是長方形的四邊所在的直線(重疊的只畫一條,因為有且只有一條):

那麼,掃描線將這張白紙分為若干個長方形。我們只需要在處理每個長方形時,對涉及到的小長方形填上一個數字(代表一種顏色)即可,而非將每一個面積為\(1\)的最小單位填色。
2). 實現
初始化
掃描完畢後,將這張紙被切割成的每個小長方形填上\(1\),表示現在是一張白紙:
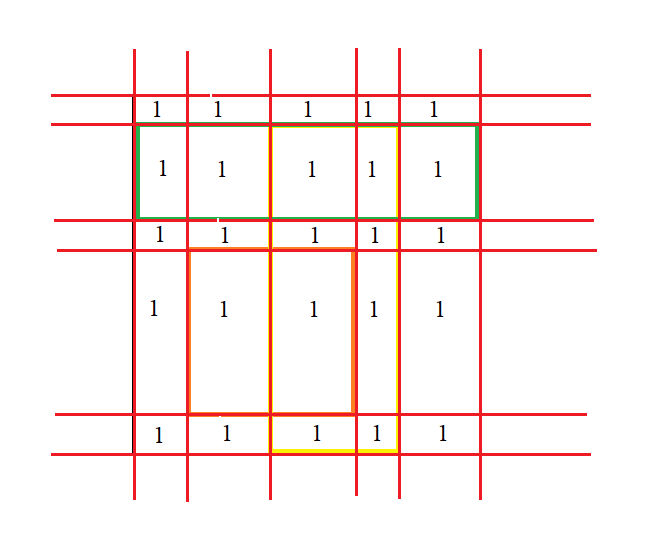
放第一個長方形
將第一個長方形涉及到的小長方形填上一個數字:
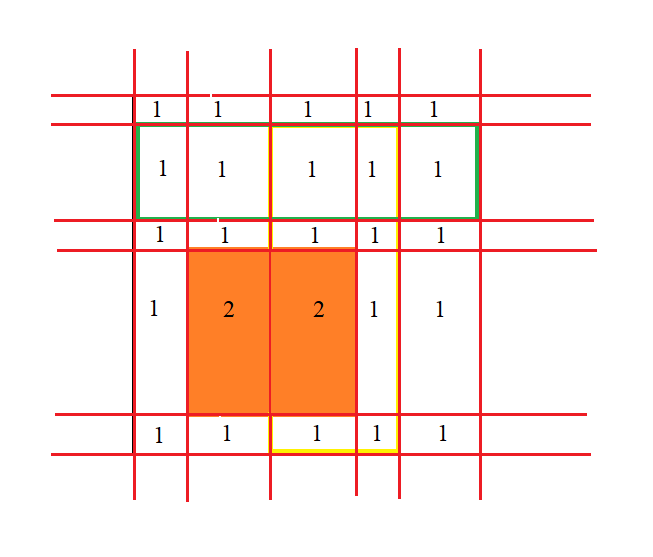
放第二個長方形
將第二個長方形涉及到的小長方形填上一個數字:
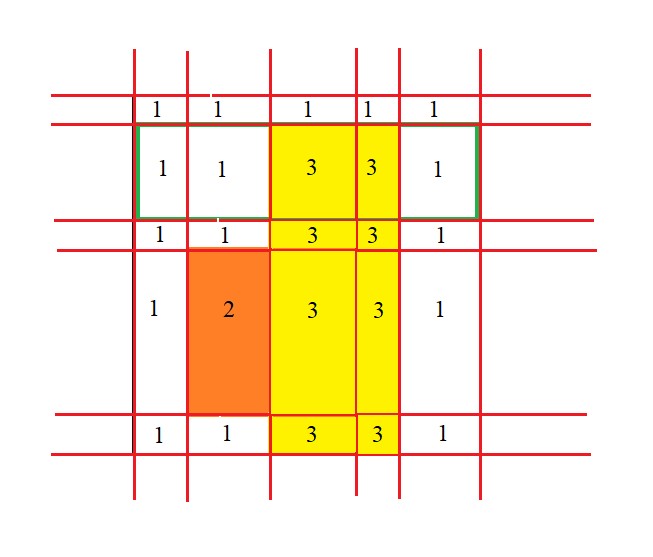
放第三個長方形
將第三個長方形涉及到的小長方形填上一個數字:
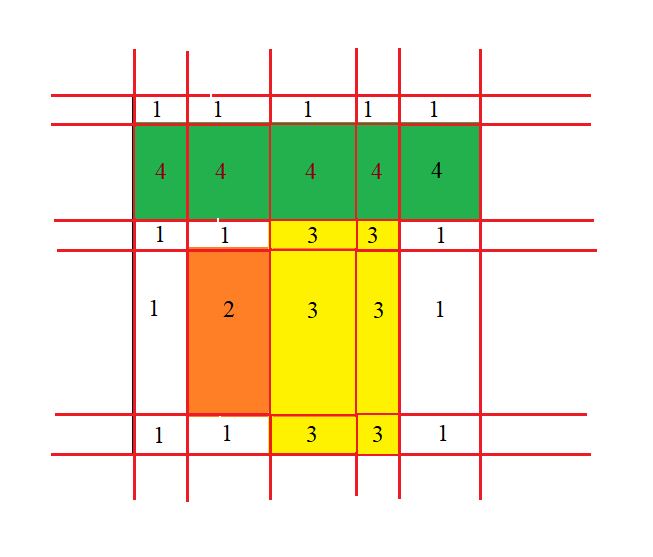
統計
一個可視顏色的總面積,就相當於所有和其顏色(數字)相等的被分割的小長方形的面積和。
三、程式框架
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1100;
const int N2 = 2200;
const int C = 2750;
const int AB = 11000;
struct node{
int llx, lly, urx, ury, color;
};
node data[N]; //data存儲每個長方形的資訊
int map[N2][N2]; //map存儲被分割(掃描)後的紙
//linex和liney存儲掃描線
//rflcx和rflcy存儲映射,即長方形的原始線對應的掃描線編號
//ans[i]表示第i號顏色的總可視面積
int linex[N2], liney[N2], rflcx[AB], rflcy[AB], ans[C];
int a, b, n, numx, numy, maxc;
int main(){
//讀入
scanf("%d%d%d", &a, &b, &n);
//讀入長方形 然後做掃描線
numx = numy = 0; maxc = 1;
for (int i = 1; i <= n; ++i) {
scanf("%d%d%d%d%d", &data[i].llx, &data[i].lly, &data[i].urx, &data[i].ury,&data[i].color);
linex[++numx] = data[i].llx;
linex[++numx] = data[i].urx;
liney[++numy] = data[i].lly;
liney[++numy] = data[i].ury;
if (maxc < data[i].color) maxc = data[i].color; //求最大顏色編號
}
//處理邊界(白紙的)掃描線
linex[++numx] = 0;
linex[++numx] = a;
liney[++numy] = 0;
liney[++numy] = b;
//排序
sort(linex + 1, linex + numx + 1);
sort(liney + 1, liney + numy + 1);
//去重
int tmp = numx; numx = 1;
for(int i = 2; i <= tmp; ++i)
if (linex[i] != linex[numx]) linex[++numx] = linex[i];
tmp = numy; numy = 1;
for(int i = 2; i <= tmp; ++i)
if (liney[i] != liney[numy]) liney[++numy] = liney[i];
//做映射
for (int i = 1; i <= numx; ++i) rflcx[linex[i]] = i;
for (int i = 1; i <= numy; ++i) rflcy[liney[i]] = i;
//初始化:全部賦值為1,表示白紙
for (int i = 1; i < numx; ++i)
for (int j = 1; j < numy; ++j) map[i][j] = 1;
//用長方形不斷進行填色
for (int k = 1; k <= n; ++k)
for (int i = rflcx[data[k].llx]; i < rflcx[data[k].urx]; ++i)
for (int j = rflcy[data[k].lly]; j < rflcy[data[k].ury]; ++j) map[i][j] = data[k].color;
//統計可視顏色面積
memset(ans, 0, sizeof ans);
for (int i = 1; i < numx; ++i)
for (int j = 1; j < numy; ++j) ans[map[i][j]] += (linex[i + 1] - linex[i]) * (liney[j + 1] - liney[j]);
//輸出答案
for (int i = 1; i <= maxc; ++i)
if (ans[i] > 0) printf("%d %d\n", i, ans[i]);
return 0;
}


