蘊含式

一、蘊含式基礎

（Ⅰ）什麼是「蘊含式」

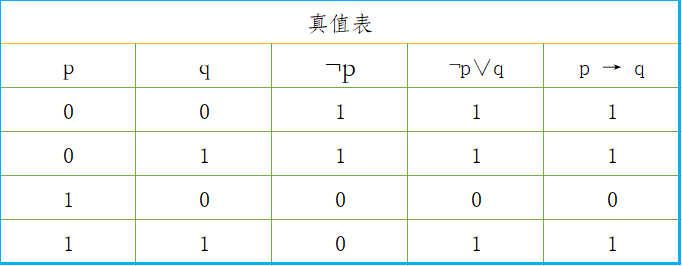
設p、q為兩個命題。複合命題「如果p，則q」稱為p與q的蘊含式，記作p→q，並稱p為蘊含式的前件，q為後件。定義中規定p→q為假當且僅當p為真q為假。

或許有同學會問：我發現這個「蘊含式」好像我們高中時所學的「命題」。自信一點，把「好像」去掉，只不過「蘊含式」比高中時所學的「命題」的範圍更廣一些。

（Ⅱ）「蘊含式」的意義

不難發現，「蘊含式」的邏輯關係為：q是p的必要條件，p是q的充分條件。也就是說諸如「只要p就q」、「q僅當p」、「只有p才q」…等，都可以符號化為p→q的形式。

（Ⅲ）「蘊含式」的真值表( True Table )

二、理解的誤區

在我們平時遇到的「p→q」要麼是p與q之間存在著一定的聯繫，要麼是在前件p為真的前提下作出的判斷。就比如我們在高中時學過的「命題」，它的形式是「若p，則q」，形式與「蘊含式」一模一樣，但是細心的同學就會發現，我們在研究問題的時候通常將前件p視為真命題，然後再來研究後件q的真假性，從而判斷「命題」真假性。所以說我們用以前高中的的思路是很難理解這個真值表（True Table）的。
　　
但是要是真想理解起來倒也不是很難，舉個栗子：這裡存在著一個蘊含式「如果我當上了班長，我將提高同學的福利」。所以不妨設，前件p為「我當上了班長」，後件q為「我將提高同學的福利」，那麼這個蘊含式就可以符號化為p→q，記為I。

所以問題就是判斷I的真假，也就是說我有沒有撒謊。

很顯然當p為真，q為假的時候，我並沒有履行我的諾言，故此時I為”False”。當p為假的時候，不管我有沒有提高同學們的福利，你都不能說我沒有履行我的諾言，因為我就沒有當上班長，此時的I為真。

三、蘊含式中的等價式

【注釋】：如果不理解，可以先康康（四），裡面有解釋為什需要學習等價式

（Ⅰ）量詞轉換律

①、「存在量詞∃」轉換為「全稱量詞∀」：¬【∀x p(x)】 ⇔ 【∃x¬p(x)】；
②、「全稱量詞∀」轉換為「存在量詞∃」：¬【∃x q(x)】 ⇔ 【∀x¬q(x)】；

（Ⅱ）含量詞的合取式、析取式的等價式

①、「全稱量詞∀」只對合取式的分配：∀x（p(x) Λ q(x)） ⇔【∀x p(x)】Λ【∀x q(x)】；
②、「存在量詞∃」只對析取式的分配：∃x（p(x)∨q(x)） ⇔ 【∃x p(x)】∨【∃x q(x)】；

（Ⅲ）量詞轄域的擴張和收縮(八個等價式)

（1）若量詞的轄域中是合取式(Λ)或者析取式(∨)，那麼對於不受約束的謂詞公式(q)可以直接進入或者退出該轄域

①、∀x（p(x) Λ q） ⇔ 【∀x p(x)】Λ q，同樣的對於∀x（p(x)∨q） ⇔ 【∀x p(x)】∨ q也成立；
②、∃x（p(x)∨q） ⇔ 【∃x p(x)】∨ q， 同樣的對於∃x（p(x)Λq） ⇔ 【∃x p(x)】Λ q也成立；

（2）若量詞的轄域中是「蘊含式」的前件，那麼作為後件的不受約束的謂詞公式不可以直接進入或者退出該轄域

①、【∀x p(x)】→ q ⇔ ¬【∀x p(x)】∨q ⇔ 【∃x¬p(x)】∨q ⇔ ∃x（¬p(x)∨q） ⇔ ∃x（p(x) → q）；
②、【∃x p(x)】→ q ⇔ ¬【∃x p(x)】∨q ⇔ 【∀x¬p(x)】∨q ⇔ ∀x（¬p(x)∨q） ⇔ ∀x（p(x) → q）；

（3）若量詞的轄域是「蘊含式」的後件，則作為前件的不受約束的謂詞公式可以直接進入或者退出該轄域

①、q → 【∀x p(x)】 ⇔ ¬q ∨【∀x p(x)】 ⇔ ∀x（¬q∨p(x)） ⇔ ∀x（q → p(x)）；
②、q → 【∃x p(x)】 ⇔ ¬q ∨【∃x p(x)】 ⇔ ∃x（¬q∨p(x)） ⇔ ∃x（q → p(x)）；

（Ⅳ）「蘊含式」 && 德摩根律

（1）普通(我願稱之為常量)「蘊含式」 && 德摩根律 的等價式

①、「蘊含式」的等價式：p→q ⇔ ¬p∨q ；
②、德摩根律：¬（p∨q） ⇔ ¬pΛ¬q ；

（2）自由元組變數在 「蘊含式」 && 德摩根律 的等價式

①、「蘊含式」的等價式：p(x)→q(x) ⇔ ¬p(x)∨q(x)；
②、德摩根律：¬（p(x)∨q(x)） ⇔ ¬p(x) Λ ¬q(x)；

（3）約束元組變數在 「蘊含式」 && 德摩根律 的等價式

①、「蘊含式」的等價式：【∀x p(x)】→【∃x q(x)】 ⇔ ¬【∀x p(x)】∨【∃x q(x)】 ⇔ 【∃x¬p(x)】∨【∃x q(x)】 ⇔ ；
②、德摩根律：¬（【∀x p(x)】∨【∃x q(x)】） ⇔ ¬【∀x p(x)】Λ¬【∃x q(x)】；

（Ⅴ）在SQL中我們重點掌握這樣幾個點：

【注釋】：在下面（四）中會解釋為什麼要這樣

（1）基礎部分（主要掌握其形式）：

①、蘊含式的等價式（其形式與x以及轄域無關）：p→q ⇔ ¬p∨q；

②、德摩根律（長橫變短橫，開口換方向）：¬（p∨q） ⇔ ¬p Λ ¬q；

③、量詞轉換律（量詞互換，命題加非），比如：¬【∀x p(x)】 ⇔ 【∃x¬p(x)】；

（2）提高部分（SQL中的條件很少有常量條件）：

①、含量詞的合取式、析取式的等價式（存在析取，全稱合取）；

②、量詞轄域的擴張和收縮（1）；

③、量詞轄域的擴張和收縮（2）（3）—— 可以根據前面的公式自己推；

（3）困難部分（常用）：

①、集合X是集合Y的父級（對於任意的x屬於X，總是存在一個y屬於Y，使得「x=y」成立）：
\(\forall\ x【x(X)\ \rightarrow\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\) ⇔ \(\forall\ x【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\) ⇔
\(\ ^¬【\ ^¬【\forall\ x【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】】】\) ⇔ \(\ ^¬【\exists\ x\ ^¬【\ ^¬x(X)\ \bigvee\ \exists\ y【y(Y)\ \bigwedge\ x=y】】】\) ⇔
\(\ ^¬【\exists\ x【x(X)\ \bigwedge\ \ ^¬【\exists\ y【y(Y)\ \bigwedge\ x=y】】】】\)。
更一般的情況，對於任意的x屬於X使得p(x)成立，總是存在一個y屬於Y，使得「q(x, y)」成立：
\(\forall\ x【p(x)\ \rightarrow\ \exists\ y\ q(x,y)】\) ⇔ \(\ ^¬【\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ y\ q(x,y)】】】\)。

②、集合X和集合Y有交集，嚴格來說就一種情況，但是為了研究「至少這個關鍵字」，我們 將此處分為兩種情況：

（ⅰ）集合X和集合Y至少有一個公共元素（某個x屬於X，總是存在一個y屬於Y，使得「x=y」成立）：
\(\exists\ x【x(X)\ \bigwedge\ \exists\ y【y(Y)\ \bigwedge\ x=y】】\)。
更一般的情況，對於某個x屬於X滿足p(x)，總是存在一個y屬於Y滿足q(x,y)：
\(\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】\)。

（ⅱ）集合X和集合Y不完全相同（存在某個x屬於X，對於任意的y只要屬於Y就必然有「x≠y」）：
首先將命題更改一下，也就是將「≠」改成「不＝」，故而有：
\(\exists\ x【x(X)\ \bigwedge\ \forall\ y【y(Y)\ \rightarrow\ \ ^¬（x=y）】】\) ⇔ \(\exists\ x【x(X)\ \bigwedge\ \ ^¬【\exists\ \ y【y(Y)\ \bigwedge\ （x=y）】】】\)。
更一般的情況，存在一個x屬於X滿足p(x)，對於任意的y只要屬於Y就必然有¬q(x,y)：\(\exists\ x【x(X)\ \bigwedge\ \forall\ y【y(Y)\ \rightarrow\ \ ^¬q(x,y)】】\) ⇔ \(\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ \ y\ q(x,y)】】\)。

③、集合X和集合Y莫得交集（對於任意的x只要屬於X，必然有對於任意的y只要屬於Y，一定滿足條件「x≠y」）：
\(\forall\ x【x(X)\ \rightarrow\ \forall\ y【y(Y) \rightarrow\ \ ^¬（x=y）】】\) ⇔ \(\forall\ x【x(X)\ \rightarrow\ \ ^¬【\exists\ y【y(Y) \bigwedge\ x=y】】】\) ⇔
\(\ ^¬【\exists\ x【x(X)\ \bigwedge\ \exists\ y【y(Y) \bigwedge\ x=y】】】\)。
更一般的情況，對於任意的x只要屬於X滿足p(x)，必然有對於任意的y只要屬於Y一定滿足條件¬q(x,y)，換一種說法就是，「對於任意的x只要屬於X滿足p(x)，必然不存在y滿足條件q(x,y)」：
\(\forall\ x【p(x)\ \rightarrow\ \ ^¬【\exists\ y\ q(x,y)】】\) ⇔ \(\ ^¬【\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】】\)。

（4）需要注意的地方：

①、必須保證「屬於」關係，比如\(x(X)\)必須滿足（原因在於最後的SQL語句……）；

②、一般情況下「\(\forall\)」後面都會加上「蘊含式\(\rightarrow\)」，「\(\exists\)」後面則很少會有蘊含式。

其實通過解讀蘊含式的含義：「只要p就有q」，不難發現在運用全稱量詞的時候，我們會運用句式「對於任意的x滿足p(x)都有q(x)成立」，這句話有一種「自然而然就綁定了」的意思：「只要x滿足p(x)那麼就會有q(x)」。
反觀存在量詞，我們用的最多的就是「總是存在一個x滿足p(x)，使得q(x)成立」，這個「使得」二字就沒有了「自然而然」的韻味了，就是一種特殊的情況，不能說x滿足p(x)後就一定有q(x)，只能是某一個x滿足p(x)後恰好也能滿足q(x)。
不過也有一種情況時存在量詞後面加上蘊含式，比如範數的某個定理（《數值分析》\(P_{163}\ 定理15\)）「如果在一種範數意義下向量序列收斂時，則在任何一種範數意義下該向量序列均收斂」，即「存在一個x滿足p(x)，必然有對於任意的x都有q(x)」，這裡的q(x)和p(x)是等價的—屬於X並且向量序列收斂：
\(\exists\ x【p(x)\ \rightarrow\ \forall\ x\ q(x)】\)。當然這個式子不能表達出推論「存在一個x不滿足p(x)，必然有對於任意的x都不滿足q(x)」，因為我們沒有辦法控制命題變換為「\(x(X)\ \bigwedge\ \ ^¬m(x)\)」，其中\(m(x)\)就是向量序列收斂。

③、在（3）.②中，求相交的時候並不是嚴格意義上的相交，因為在（ⅰ）中包含了（3）.①的情況，在（ⅱ）中包含了（3）.③的情況。但是這並沒有影響到我們使用，因為我們一般遇到的相交的問題都是「至少」問題，不會說讓我們求「集合X和Y有共同的非空元素，並且兩集合不互相包含」，這樣很噁心，而解決「至少」的問題一般會用其否命題「全部」問題求非來解決，所以我們就不用考慮嚴格意義上的相交了。
但是話又說回來，如果真的遇上了就在（3）.②.（ⅰ）和（3）.②.（ⅱ）之間加上合取式：
\(\exists\ x【p(x)\ \bigwedge\ \exists\ y\ q(x,y)】\quad\bigwedge\quad\exists\ x【p(x)\ \bigwedge\ \ ^¬【\exists\ \ y\ q(x,y)】】\)。但是千萬注意存在量詞只能對析取式進行分配。

④、【注意：】

（ⅰ）「全稱量詞∀」可以對合取式進行分配，但是不能對析取式進行分配。
這句話從另一角度上來說：\(【\forall\ x\ p(x)】\) ⇔ \(p(a_1)\bigwedge…\bigwedge p(a_n)\)；

（ⅱ）「存在量詞∃」可以對析取式進行分配，但是不能對合取式進行分配。
這句話從另一角度上來說：\(【\exists\ x\ p(x)】\) ⇔ \(p(a_1)\bigvee…\bigvee p(a_n)\)；

四、所以說……我到底想要表達什麼？

​ 當某一個命題為條件命題(也就是「蘊含式」)的時候，記為p→q。這所表達的意思就是：當p為真並且p→q也為真的情況下(這一前提常常被人們忽略，認為這是理所當然的)，發生了p事件就一定能發生q事件。我們將p和q視為兩個集合，不難理解，這時就能得到p⊆q。

​ 所以表示兩個集合是父子集合的時候，可以這樣來表述：\(\forall\ x【p(x)\in P \rightarrow \exists\ y【q(y)\in Q\ \bigwedge\ p(x)=q(y)】】\)。
我們可以這樣來分析一下：

①、\(\forall\ x【Condition】\) —— 對於任意的x都要滿足某個條件，這個條件用Condition來代指；
②、\(Condition\)：\(p(x)\in P \rightarrow \exists\ y【q(y)\in Q\ \bigwedge\ p(x)=q(y)】\) —— 這個條件是：只要p(x)屬於P集合中，那麼總能找到某一個y,使得q(y)屬於Q集合,並且有p(x)=q(y)成立；

​ 很好理解吧，但是這裡我並不只是bb離散數學，而是要將這玩意兒和SQL的實際情況相結合。在SQL中有一個很巧妙但是讓人們感到十分蛋疼的一個機制：沒有「全稱量詞∀」。這時我們就需要運用上面所學到的相關知識，將這些「全稱量詞∀」轉換為「存在量詞∃」。怎樣表述命題之間的關係、怎樣轉換為不含「全稱量詞∀」的命題，這些在（三）中已經有所了解了，那我們來看下面一個實例。

訴求：查詢選修了全部課程的學生的姓名和學號。

元組關係運算的表達式：
\(\{new\_s^{(2)}\) |
　　\(\exists\ s\)【 # 總是存在一個s滿足條件：
　　　　\(s(S)\ \bigwedge\) # s∈S
　　　　\(\forall\ c【c(C) \rightarrow\) # 對於任意的c滿足條件：只要c∈C，那麼一定有存在某個sc滿足條件：
　　　　　　\(\exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】\) # sc∈SC，並且使得sc.sno = s.sno和sc.cno = c.cno同時成立 —— 意思就是C.CNo集合是SC.CNo集合的子集，並且將這個集合連接起來；
　　　　】
　　】 Λ
　　\(new\_s[1] = s[1]\ \bigwedge\)
　　\(new\_s[2] = s[2]\)
\(\}\)。

​ 但是終究不能用元組關係演算來進行篩選，還得轉換為SQL標準語言。用到（三）中的公式：

（1）首先將元組關係演算分解、簡化：∃s, s(S) Λ p，即為存在s滿足條件：s∈S，並且p；
【注釋】：其中的p為「\(\forall\ c【c(C)\ \rightarrow\ \exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】\)」。

（2）其次將歸屬關係p(P)盡量去掉，進一步簡化，因為歸屬關係在SQL統一用「SELECT 欄位名 FROM 表」來表述；
【注釋】：其中p為「\(\forall\ c【c(C)\ \rightarrow\ \exists\ sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】\)」。

（3）靈活運用「蘊含式」公式，將能合併的合併，使得最後的形式為：
\(\exists\ p_1【Conditions\ \bigwedge\ \exists\ p_2【Conditions\ \bigwedge\ 【…\exists\ p_n【Conditions】】】】\)。那麼根據這一點將p化簡就有：

\[\begin{aligned}
p &= \forall\ c【\ ^¬c(C)\ \or\ \exist\ sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】\\
&= \forall\ c【\exist\ sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】\\
&= \ ^¬【\exist\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \and\ sc.cno = c.cno】】】\\
\end{aligned}
\]

（4）所以最後的形式為：\(\exists\ s\ \ ^¬【\exists\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】】\)。

​ 轉換為SQL語句：

SELECT SNo, SN
FROM S
WHERE
	NOT EXISTS (
		SELECT *
		FROM C
		WHERE  
			NOT EXISTS (
				SELECT *
				FROM SC
				WHERE CNo = C.CNo AND SNo = S.SNo
			)
    )    

​ 這裡其實有一個很容易弄錯的地方：誤以為連接SC表和S表的元組變數要單獨寫一個「\(\exists\ sc【sc(SC)\ \bigwedge\ sc.sno = s.sno】\)」，也就是說將兩個表間的連接獨立開，各連各的。這個想法非常的幼稚，為什麼這樣說呢，打一個形象的比方：S表相當於左邊的一個岸，C表相當於右邊的一個岸，SC表顯然就是連接兩岸的橋，如果說想要用SC表將C表和S表連起來，那麼肯定就需要找到同一個SC表中的元組sc，讓它左手牽S表的元組s，同時右手牽著C表的元組c；如果這不是同時牽的話，就很可能導致橋不是同一個橋，即不是同一個sc元組。下面我們是可以通過簡單的邏輯證明來表述的。如果我們將這兩個連接獨立，則會得到：

①、\(p = \exists\ sc【sc.sno = s.sno】\)；

②、按照上述4個步驟簡化q表達式

\[\begin{aligned}
q =\qquad &\forall\ c【\ ^¬c(C)\ \or\ \exist\ sc【sc.cno = c.cno】】\\
\overset{去歸屬關係}{\Longrightarrow} &\forall\ c【\exist\ sc【sc.cno = c.cno】】\\
\overset{轉變全稱量詞}{\Longrightarrow} &\ ^¬【\exist\ c \ ^¬【\exist\ sc【sc.cno = c.cno】】】
\end{aligned}
\]

③、現在的形式為：∃s【p Λ q】,但是並不是「存在量詞∃」的迭代形式，還需要進一步合併；

④、由德摩根律得：p Λ q = ¬(¬p ∨ ¬q) = ¬(p → ¬q)；

⑤、將p、q代入得：\(\ ^¬【\exists\ sc\ sc.sno = s.sno\ \rightarrow\ \exists\ c\ \ ^¬【\exists\ sc\ sc.cno = c.cno】】\)；

⑥、由「量詞轄域的擴張和收縮」的第三點，前件不受∃c的轄域，所以可以等價為：
\(\ ^¬【\exists\ c\ 【【\exists\ sc\ sc.sno = s.sno】\ \rightarrow\ \ ^¬【\exists\ sc\ sc.cno = c.cno】】】\) ⇔
\(\ ^¬【\exists\ c\ 【\ ^¬【∃sc\ sc.sno = s.sno】\ \bigvee\ \ ^¬【∃sc\ sc.cno = c.cno】】】\)) ⇔
\(\ ^¬【\exists\ c\ \ ^¬【【∃sc\ sc.sno = s.sno】\ \bigwedge\ 【∃sc\ sc.cno = c.cno】】】\)

⑦、很多同學就會將這個等價與「\(\ ^¬【\exists\ c\ \ ^¬【∃sc【sc.sno = s.sno\ \bigwedge\ sc.cno = c.cno】】】\)」結果好像是一模一樣，但是這裡其實是有一個很大的邏輯錯誤：由「含量詞的合取式、析取式的等價式」的注意事項，我們知道「存在量詞∃」只能對析取式進行分配、不能對合取式進行分配。這是因為
「\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)」和「\(\exists\ x【p(x)\ \bigwedge\ q(x)】\)」之間的關係是「蘊含式」。
我們可以簡單的來證明一下：

（1）從左到右：假設前件「\(\exists\ x【p(x)\ \bigwedge\ q(x)】\)」為真，那麼存在一個x=c，使得p(c)Λq(c)為真，即存在一個x=c使得p(c)為真，存在一個x=c使得q(c)也為真；故而後件「\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)」為真；

（2）從右到左：假設後件「\(【\exists\ x\ p(x)】\ \bigwedge\ 【\exists\ x\ q(x)】\)」為真，那麼我們只能得到，存在一個x=c使得p(c)為真，存在一個x=b使得q(b)為真，並不能保證b=c，所以由後件得不到前件；

五、總結

（Ⅰ）掌握「蘊含式」，以及什麼時候運用；
提示：等價式、德摩根律、收縮與擴張，當表示一個集合是另一個集合的子集時運用「蘊含式」。

（Ⅱ）充分理解「含量詞的合取式、析取式的等價式」，從而得出結論：不能將連接操作分開寫，必須寫在一起，這裡的一起是指：保證連接時的元組是同一個。具體表現為：寫在靠後的\(WHERE\)語句中，因為要包含較多的\(SELECT\)語句(本質上是表)，使得選擇元組是同一個；
提示：「全稱量詞∀」只可以對合取式進行分配；「存在量詞∃」只可以對析取式進行分配。

六、實例

（1）案例_01_以全部課程為準，學生的4種選課情況；

（2）案例_02_以’李力’老師教授的課程為準，學生的5種選課情況；

（3）案例_03_以’資料庫’和’JAVA’_教師姓名、編號為準，老師授課的4種選課情況；

（4）案例_04_以全部學生為準，課程被選的4種選課情況(只列舉出2種)；

（5）案例_05_關於：至少、至多、恰好；