JavaScript圖形實例:Hilbert曲線
- 2020 年 7 月 6 日
- 筆記
- JavaScript程式設計
德國數學家David Hilbert在1891年構造了一種曲線,首先把一個正方形等分成四個小正方形,依次從西北角的正方形中心出發往南到西南正方形中心,再往東到東南角的正方形中心,再往北到東北角正方形中心,這是一次迭代;如果對四個小正方形繼續上述過程,往下劃分,反覆進行,最終就得到一條可以填滿整個正方形的曲線,這就是Hibert曲線。其生成過程如圖1所示。
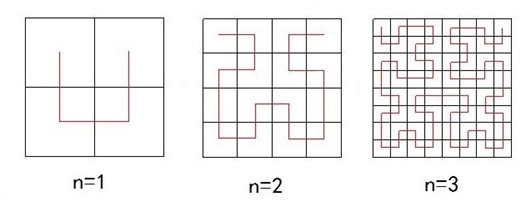
圖1 Hilbert曲線的生成
Hilbert曲線可以採用遞歸過程實現,在遞歸處理時,連接中點的方式有4種,如圖2所示。
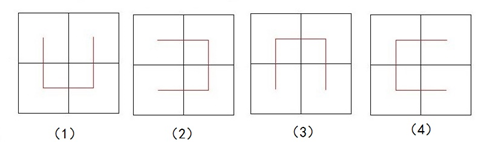
圖2 連接中心點的4種方式
設正方形左上角的頂點坐標為(x1,y1),右下角頂點坐標為(x2,y2)。若將方式(3)的正方形左上角坐標置為(x2,y2),右下角坐標置為(x1,y1),則方式(3)等同於方式(1),相當於旋轉180°;同理,方式(4)等同於方式(2)。因此,4種連接中心點的方式可以看成(1)和(2)兩種。
兩種連線方式的連線走向及下一次擴展的方式如圖3所示。

圖3 兩種連線方式走向及擴展
其中,方式(1)的四個中心點坐標分別為:
①(x1+dx/4,y1+dy/4) ②(x1+dx/4, y1+3*dy/4)
③ (x1+3*dx/4, y1+3*dy/4) ④(x1+3*dx/4,y1+dy/4) (dx=x2-1,dy=y2-y1)
方式(2)的四個中心點坐標分別為:
①(x1+dx/4,y1+dy/4) ②(x1+3*dx/4,y1+dy/4)
③ (x1+3*dx/4, y1+3*dy/4) ④(x1+dx/4, y1+3*dy/4)
為此,引入一個標識變數s,s=1表示方式(1),s=-1表示方式(2),這樣兩種方式的中心點坐標可以統一表示為:
①(x1+dx/4,y1+dy/4) ②(x1+(2-s)*dx/4, y1+(2+s)*dy/4)
③(x1+3*dx/4, y1+3*dy/4) ④(x1+(2+s)*dx/4,y1+(2-s)*dy/4)
遞歸擴展時,方式(1)中4個小正方形的擴展方式分別是:方式(2)、方式(1)、方式(1)和方式(4)(注意:給定兩個頂點坐標順序調整後等同於方式(2));方式(2)中4個小正方形的擴展方式分別是:方式(1)、方式(2)、方式(2)和方式(3)。
編寫如下的HTML程式碼。
<!DOCTYPE html>
<head>
<title>Hilbert曲線</title>
</head>
<body>
<canvas id=”myCanvas” width=”500″ height=”500″ style=”border:3px double #996633;”>
</canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
var depth=5;
ctx.lineWidth = 2;
ctx.strokeStyle = “red”;
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 – x1,
dy = y2 – y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
</script>
</body>
</html>
在瀏覽器中打開包含這段HTML程式碼的html文件,可以看到在瀏覽器窗口中繪製出如圖4所示的Hilbert曲線。

圖4 遞歸深度maxdepth =5的Hilbert曲線
上面的程式需要推出方式(一)和方式(二)的坐標統一形式,還需注意方式(3)和方式(4)與方式(一)和方式(二)的同一性。
由於Hilbert曲線可以看成是4種方式進行組合,因此可以直接對4種方式編寫遞歸過程。編寫如下的HTML文件。
<!DOCTYPE html>
<head>
<title>Hilbert曲線</title>
</head>
<body>
<canvas id=”myCanvas” width=”500″ height=”500″ style=”border:3px double #996633;”>
</canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
ctx.lineWidth = 2;
ctx.strokeStyle = “red”;
ctx.beginPath();
var depth=5; // 遞歸深度
var h=400/Math.pow(2,depth);
var x = 50+h;
var y = 50+h;
ctx.moveTo(x,y);
One(depth);
ctx.stroke();
function One(n) // 方式(1)的遞歸調用
{
if(n > 0)
{
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
One(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
}
}
function Two(n) // 方式(2)的遞歸調用
{
if(n > 0)
{
One(n-1);
ctx.lineTo(x+h, y); x+=h;
Two(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
}
}
function Three(n) // 方式(3)的遞歸調用
{
if(n > 0)
{
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Three(n-1);
ctx.lineTo(x-h, y); x-=h;
Three(n-1);
ctx.lineTo(x, y+h); y+=h;
Two(n-1);
}
}
function Four(n) // 方式(4)的遞歸調用
{
if(n > 0)
{
Three(n-1);
ctx.lineTo(x-h,y); x-=h;
Four(n-1);
ctx.lineTo(x, y-h); y-=h;
Four(n-1);
ctx.lineTo(x+h, y); x+=h;
One(n-1);
}
}
</script>
</body>
</html>
在瀏覽器中打開包含這段HTML程式碼的html文件,可以看到在瀏覽器窗口中繪製出如圖5所示的Hilbert曲線。

圖5 調用One(depth)時繪製的圖形
將程式中的調用語句「One(depth)」改寫成「Two(depth)」,則在瀏覽器窗口中繪製出如圖6所示的Hilbert曲線。這個圖形可以看成是圖5向左旋轉90°得到的。實際上,由圖2可知,將方式(一)的圖形向左旋轉90°得到的就是方式(二)的圖形。

圖6 調用Two(depth)時繪製的圖形
將程式中調用語句「One(depth)」改寫成「Three(depth)」,同時修改初始坐標為
「var x = 450-h; var y = 450-h;」,則在瀏覽器窗口中繪製出如圖7所示的Hilbert曲線。

圖7 調用THree(depth)時繪製的圖形
將程式中調用語句「One(depth)」改寫成「Four(depth);」,同時修改初始坐標為
「var x = 450-h; var y = 450-h;」,則在瀏覽器窗口中繪製出如圖8所示的Hilbert曲線。

圖8 調用Four(depth)時繪製的圖形
將Hilbert曲線的生成過程進行動畫展示,編寫如下的HTML程式碼。
<!DOCTYPE>
<html>
<head>
<title>Hilbert曲線</title>
</head>
<body>
<canvas id=”myCanvas” width=”500″ height=”500″ style=”border:3px double #996633;”></canvas>
<script type=”text/javascript”>
var canvas = document.getElementById(‘myCanvas’);
var ctx = canvas.getContext(‘2d’);
var depth=1;
function drawShapes(n,s,x1,y1,x2,y2)
{
dx = x2 – x1,
dy = y2 – y1;
if (n>1)
{
if(s>0)
{
drawShapes(n-1,-1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,1,x1,(y1+y2)/2,(x1+x2)/2,y2);
drawShapes(n-1,1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,-1,x2,(y1+y2)/2,(x1+x2)/2,y1);
}
else
{
drawShapes(n-1,1,x1,y1,(x1+x2)/2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,y1,x2,(y1+y2)/2);
drawShapes(n-1,-1,(x1+x2)/2,(y1+y2)/2,x2,y2);
drawShapes(n-1,1,(x1+x2)/2,y2,x1,(y1+y2)/2);
}
}
if (n==1)
{
ctx.lineTo(x1+dx/4,y1+dy/4);
ctx.lineTo(x1+(2-s)*dx/4, y1+(2+s)*dy/4);
ctx.lineTo(x1+3*dx/4, y1+3*dy/4);
ctx.lineTo(x1+(2+s)*dx/4,y1+(2-s)*dy/4);
}
}
function go()
{
ctx.clearRect(0,0,canvas.width,canvas.height);
ctx.lineWidth = 2;
ctx.strokeStyle = “red”;
ctx.beginPath();
ctx.moveTo(50+400/Math.pow(2,depth+1),50+400/Math.pow(2,depth+1));
drawShapes(depth,1,50,50,450,450);
ctx.stroke();
depth++;
if (depth>6)
{
depth=1;
}
}
window.setInterval(‘go()’, 1000);
</script>
</body>
</html>
在瀏覽器中打開包含這段HTML程式碼的html文件,可以看到在瀏覽器窗口中呈現出如圖9所示的Hilbert曲線動態生成效果。

圖9 Hilbert曲線動態生成


