基於公共子序列的軌跡聚類(c#)
- 2019 年 10 月 12 日
- 筆記
前言
如今的世界中,想要研究人們的出行活動,可以利用智慧手機或智慧手環等個人設備生成的 GPS 數據進行研究。而在眾多的研究方向中,出行的熱點路線或者說經常出行的路線也比較受歡迎。採用熱力圖的方式對其進行研究具有許多優點。熱力圖給使用者的感覺就是特別直觀,一眼便看出來哪些路徑屬於熱跡(我們把熱點路線,也就是重複度高的路線稱為熱跡)。如下圖所示:
 (圖片來自網上,侵刪)
(圖片來自網上,侵刪)
從圖中我們一眼便能夠找出兩條粗壯的熱跡。這表示有某種物體經常沿著兩條路線運動。但對於電腦來說,要從圖中找出這兩條熱跡,並加以區分形成兩條完整的路線可不是一件容易的事。所以我們只能直接從軌跡上入手。接下來將介紹利用公共子序列進行軌跡聚類的方法。
該聚類方法的核心思想是相似的軌跡在地理空間中佔有的位置基本一致,軌跡越相似其共有的位置占原軌跡空間的比重越大,並且隨著我們劃分軌跡的精度降低而提高。
數據準備
Gps 數據準備
研究軌跡聚類,最基本的要求就是擁有大量的軌跡數據。幸運的,我從網上的項目中找到了公開的 Gps 數據。為什麼說是幸運的?在此之前,我曾寫過一個 App,以期收集自己的出行軌跡進行研究。該應用的確達到了預期,但困難的是手機要開啟 Gps 才能得到比較精準的軌跡數據,這顯然提高了手機電量的要求。除此之外,收集眾多的軌跡需要大量時間、上班族軌跡相對固定等一系列因素導致收集自己的軌跡計劃夭折。而在網上找到的數據完全滿足研究要求。這些數據來自於微軟亞洲研究院的項目 Geolife,是每個人都能夠獲取的。該數據以 plt 為文件後綴存儲,但實際上就是普通的文本文件,並且除了前六行外就是 csv 格式的。
軌跡數據模型類
這是本項目中用到的數據類模型
//軌跡數據點通用模型(以介面定義) public interface IGeoInfoModel { float Latitude { get; set; } float Longitude { get; set; } } //軌跡類 public class Trajectory { public Guid Id { get; } public Trajectory() { Id = Guid.NewGuid(); } public string Name { get; set; } public List<IGeoInfoModel> GeoPoints { get; set; }//軌跡點集 public List<string> GeoCodes { get; set; }//軌跡編碼集 public Trajectory Parent { get; set; }//軌跡的父親 //軌跡的兄弟姐妹,該集合中的軌跡與該軌跡相似度極高(執行緒安全集合) public ConcurrentBag<Trajectory> Siblings { get; } = new ConcurrentBag<Trajectory>(); //軌跡的後輩,該集合中的軌跡與該軌跡具有一定相似性,但低於兄弟姐妹(執行緒安全集合) public ConcurrentBag<Trajectory> Children { get; } = new ConcurrentBag<Trajectory>(); public float MinLat => GeoPoints.Min(t => t.Latitude); public float MinLon => GeoPoints.Min(t => t.Longitude); public float MaxLat => GeoPoints.Max(t => t.Latitude); public float MaxLon => GeoPoints.Max(t => t.Longitude); public int Level { get; set; }//軌跡在族譜中的代數/層數 public string LevelTag { get; set; }//代數標籤,用於列印 }軌跡序列產生(軌跡的低解析度/低精度描述)
要找軌跡間的公共子序列,首先得有可以描述軌跡的序列的方法。該序列具有比原始軌跡低的精度,但基本可以描述一條軌跡的空間位置。下面介紹兩種該項目中用到的編碼方法。
保留高位小數法
最簡單的就是僅保留經緯度的高位小數來進行編碼。這種方式的產生的數據的精度調節有限,但也能滿足一般需求。以坐標(1.2222,33.44444)來說保留三位小數後可得「1.222_33.444」,中間添加下劃線是保留反解碼的需求。
var digits = 3; var dig = $"F{digits}"; var code = $"{t.Latitude.ToString(dig)}_{t.Longitude.ToString(dig)}"GeoHash 法
GeoHash 是公認的計算經緯度編碼的有效方法,並且精度調節能力較強。讀者可以從這裡進行了解Geohash 精度和原理。除此之外,GeoHash 可以得到較短的字元串,還是以坐標(1.2222,33.44444)來說,得到 7 位的字元編碼「s8pycn3」。該hash碼精度和直接取上面取三位小數的方式上精度接近,但字元長卻縮減了 5 位。這利於高效的查找公共子序列。在 c#中我們直接 nuget 命令添加 nupkg 包NGeoHash.DotNetCore即可獲得 GeoHash 的計算方法。
var code = GeoHash.Encode(1.2222,33.44444, 7);子序列的最終形式
上述兩種方法皆可得到描述軌跡的序列。對於我們的公共子序列聚類來說,我們使用 GeoHash 得到軌跡序列能夠得到較高的效率(花費時間基本為保留高位小數法的 60%)。此外需要注意的就是:1.該聚類方法並不關心軌跡點的先後順序,也就是時間無關性;2.產生的軌跡序列會有重複值,但我們只關心軌跡是否在某一空間,而不關心在某一空間出現的次數,也就是重複無用性。基於以上兩點,初步產生的軌跡序列需要去重,這對於查找公共子序列來說也是一種效率優化。
這對於 c#來說是極其簡單的:
//並行迭代軌跡獲得軌跡序列 Parallel.ForEach(tracks, t => { // t.GeoCodes = GeoHelper.GetGeoCodes(t.GeoPoints, 3).ToList();//保留高位小數法 t.GeoCodes = t.GeoPoints .Select(tt => GeoHash.Encode(tt.Latitude, tt.Longitude, 7)) .Distinct() .ToList();//GeoHash法 });軌跡相似度的計算
在得到每條軌跡的序列基礎上,我們可以進行軌跡的相似度計算。而軌跡相似度可以歸結為軌跡序列間的公共子序列占原始序列的比率。
//array為軌跡列表,ibf為索引1,jaf為索引2,計算GeoCodes的交集 var intersect = array[ibf].GeoCodes.Intersect(array[jaf].GeoCodes).ToList(); //公共子序列的個數轉為浮點型,避免下一步計算為整形時結果直接歸零 var intersectCount = (float) intersect.Count; //公共軌跡(子序列)的與軌跡1的相似度 var rateIbf = intersectCount / array[ibf].GeoCodes.Count; //公共軌跡(子序列)的與軌跡2的相似度 var rateJaf = intersectCount / array[jaf].GeoCodes.Count;軌跡族譜的生成
得到軌跡相似度後,我們定義了兩個閾值:一個為兄弟姐妹相似度scaleSimilar,一個為後代相似度scaleBlood。注意,兄弟姐妹相似度總是比後代相似度的值要大。根據這兩個閾值,我們可以進行軌跡族譜的生成。如果相似度rateIbf和rateJaf都大於scaleSimilar,說明兩條軌跡極為相似,被定義為兄弟姐妹。如果都大於scaleBlood,並且rateIbf大於rateJaf,則軌跡 2 是 1 的後代,反之 1 是 2 的後代。
以下是這個演算法的核心:
//構建軌跡樹(族譜) public IEnumerable<Trajectory> BuildClusterTree(IEnumerable<Trajectory> trajectories, float scaleSimilar = 0.8f, float scaleBlood = 0.6f) { var array = trajectories.OrderByDescending(t => t.GeoCodes.Count).ToArray(); for (var ibf = 0; ibf < array.Length; ibf++) { Parallel.For(ibf + 1, array.Length, jaf => { if (array[jaf].Level == 1) return; var intersect = array[ibf].GeoCodes.Intersect(array[jaf].GeoCodes).ToList(); var intersectCount = (float) intersect.Count; var rateIbf = intersectCount / array[ibf].GeoCodes.Count; var rateJaf = intersectCount / array[jaf].GeoCodes.Count; if (rateIbf >= scaleSimilar && rateJaf >= scaleSimilar) { array[jaf].Level = 1; array[ibf].Siblings.Add(array[jaf]); array[jaf].Siblings.Add(array[ibf]); } else if (rateJaf > rateIbf && rateIbf >= scaleBlood) { array[jaf].Level = 1; array[jaf].Parent = array[ibf]; array[ibf].Children.Add(array[jaf]); } else if (rateIbf > rateJaf && rateJaf >= scaleBlood) { array[ibf].Level = 1; array[ibf].Parent = array[jaf]; array[jaf].Children.Add(array[ibf]); } }); } var root = array.Where(t => t.Level == 0 ).ToList(); SetClusterTreeLevelInfo(root); return root; } //設置代數及標籤資訊 private void SetClusterTreeLevelInfo(IEnumerable<Trajectory> tree,int level = 0, string levelTag = "") { Parallel.For(0, tree.Count(), i => { var node = tree.ElementAt(i); node.Level = level; node.LevelTag = $"{levelTag}{i}"; for (var j = 0; j < node.Siblings.Count; j++) { var sib = node.Siblings.ElementAt(j); sib.Level = level; sib.LevelTag = $"{node.LevelTag}__{j}_sim"; } SetClusterTreeLevelInfo(node.Children, level + 1, $"{node.LevelTag}_"); }); }結果展示及說明
我們直接上最終的軌跡族譜圖的展示
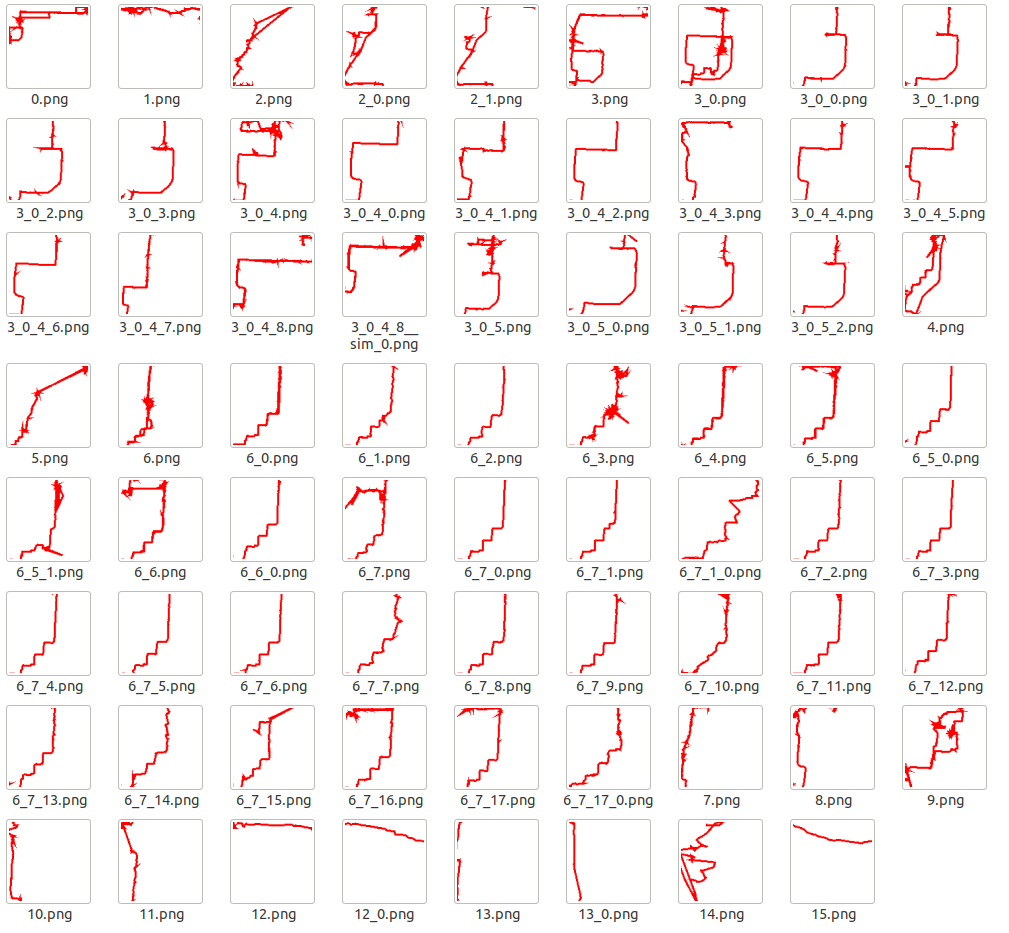
讀者放大後應該能夠看清圖片的文件名,文件名是代數標籤。以「3.png」和「3_0.png」來說,「3.png」是「3_0.png」的父親。對應的,後者是前者的孩子(所有軌跡對於都是自適應固定大小的圖片畫的,所以縮放比例和整體偏移會導致看起來有差別。讀者仔細觀察能夠發現 3_0 只是 3 的左下角一部分)。而對於「3_0_4_8.png」和「3_0_4_8__sim_0.png」來說則互為兄弟姐妹(縮略圖與自適應的確影響了結果的查看)。
此外,我們能夠看出第 3 和第 6 是兩個大家族。如果利用所有軌跡的數據生成熱力圖,那麼 3 族和 6 族所經過的地方熱力值相對來說要高很多。把一個大家族的所有成員軌跡疊加後可以得到我們想要的熱跡。
總結
該演算法如果不用並行計算是一個時間複雜度為:O(n^2)的演算法「n(n+1)/2」。而改為並行計算後,效率有很大提升(由於直接採用並行計算,不知道提升了多少)。示例中71條軌跡生成族譜樹僅需25毫秒左右,而1988條軌跡需要7.5秒左右。從效率和結果上來說都達到了令人滿意的程度。另外,該項目已經上傳github,訪問請點擊QianMo,歡迎大家提出修改意見。

