傳統聲學模型之HMM和GMM

聲學模型是指給定聲學符號(音素)的情況下對音頻特徵建立的模型。

數學表達

用 \(X\) 表示音頻特徵向量 (觀察向量)，用 \(S\) 表示音素 (隱藏/內部狀態)，聲學模型表示為 \(P(X|S)\)。

但我們的機器是個牙牙學語的孩子，並不知道哪個音素具體的發出的聲音是怎麼樣的。我們只能通過大量的數據去教他，比如說在拼音「é」的時候對應「鵝」的發音，而這個過程就是 GMM 所做的，根據數據建立起「é」這個拼音對應的音頻特徵分布，即 \(P(x|s=é)\)。孩子學會每個拼音的發音後，就可以根據拼音拼讀一個單詞 / 一個句子，但你發現他在讀某段句子的時候，聽起來好像怪怪的，你檢查發現是他把某個拼音讀錯了，導致這句話聽起來和常理不符。而這個怪怪的程度就是你聽到這個音頻特徵序列的時感覺這個音頻序列以及其背後的拼音出現的可能性的倒數，這部分則是通過 HMM 來建模的。

總結一下，GMM 用於對音素所對應的音頻特徵分布進行建模，HMM 則用於音素轉移和音素對應輸出音頻特徵之間關係的建模。

HMM

即為隱馬爾可夫模型（Hidden Markov model，HMM）

HMM 脫胎於馬爾可夫鏈，馬爾可夫鏈表示的是一個系統中，從一個狀態轉移到另一個狀態的所有可能性。但因為在實際應用過程中，並不是所有狀態都是可觀察的，不過我們可以通過可觀察到的狀態與隱藏狀態之間的可能性。因此就有了隱馬爾可夫模型。

HMM 要遵循的假設：

  • 一階馬爾可夫假設：下一個狀態只依賴於當前的狀態。因此多階馬爾可夫鏈可簡化為

    \[P(s_{t+1} | s_1,s_2,\ldots,s_t) = P(s_{t+1} | s_t)
    \]

  • 輸出無關假設：每個輸出只取決於當前 (內部/隱藏) 狀態，和前一個或多個輸出無關。

聲學模型為什麼要用HMM？

因為聲學模型建立的是在給定音素序列下輸出特定音頻特徵序列的似然 \(P(X|S)\)，但在實際情況中，我們只知道音頻特徵序列，並不知道其對應的音素序列，所以我們需要通過 HMM 建立音頻特徵與背後的每個音素的對應關係，以及這個音素序列是怎麼由各個音素組成的。

上兩個假設可以引申出 HMM 中主要的兩種概率構成：

  • 從一個內部狀態 \(i\) 轉移到另一個內部狀態 \(j\) 的概率稱為轉移(Transition) 概率，表示為 \(a_{ij}\)。
  • 在給定一個內部狀態 \(j\) 的情況下觀察到某個觀察值 \(x_t\) 的概率稱為輸出(Emission)概率，表示為 \(b_j(x_t)\)。

HMM 的三個經典問題

  • 評估問題 Estimation
  • 解碼問題 Decoding
  • 訓練問題 Learning

⚠️：後文提到的狀態即指的是內部 / 隱藏狀態。

評估問題

評估問題就是說，我已知模型參數 \(\theta\) (輸出概率以及轉移概率)，最後得到的觀察序列為某個特定序列 \(X\) 的概率是多少。

在剛才的例子中，就是孩子已經知道每個拼音後面可能接什麼拼音，每個拼音怎麼讀，當他讀出了某段聲音，這段聲音的概率是多少。

因為在觀察序列固定的情況下，有多種可能的狀態序列 \(S\)，而評估問題就是要計算出在所有可能的狀態下得到觀察序列的概率，表示為

\[\begin{aligned}
P(X) = \sum_S P(X | S) P(S) \\
\end{aligned}
\]

在當前的公式里，我們暫時先忽略固定的參數 \(\theta\)。根據一階馬爾可夫假設，時刻 \(t\) 的狀態都只取決於時刻 t-1 的狀態，因此單個狀態序列出現的概率表示為

\[\begin{aligned}
P(S) &= P(s_1) \prod^T_{t=2} P(s_t|s_{t-1}) \\
&= \pi_k \prod^T_{t=2} a_{ij}
\end{aligned}
\]

其中， \(\pi_k\) 表示時刻1下狀態為 \(k\) 的概率。

根據輸出無關假設，在時刻 \(t\) 觀察序列的值只取決於時刻 \(t\) 的狀態，因此觀察序列關於狀態序列的似然表示為

\[P(X|S) = \prod_{t=1}^T P(x_t|s_t) = \prod_{t=1}^T b_j(x_t)
\]

因此整個觀察序列出現的概率為

\[\begin{aligned}
P(X) &= \sum_S P(X | S) P(S) \\
&= \sum_S \pi_k b_k(x_1) \prod^T_{t=2} a_{ij} b_j(x_t)
\end{aligned}
\]

由於 \(i,j,k\) 都表示可能的狀態，假設有 \(n\) 種狀態，那麼計算該概率的事件複雜度就為 \(O(n^T)\)，可謂是指數級別了。

因此，前人開動了腦筋，提出了在該問題上將時間複雜度將為多項式時間的方法。

似然前向演算法

該方法採用了分治 / 動態規劃的思想，在時刻 \(t\) 下的結果可以利用時刻 \(t-1\) 的結果來計算。

在時刻 \(t\)，觀察序列的概率表示為前 \(t\) 個時刻的觀察序列與時刻 \(t\) 所有可能的狀態同時出現的概率和

\[P(x_1,x_2,\ldots,x_t) = \sum_{j\in N} P(x_1,x_2,\ldots,x_t,s_t=j)
\]

其中， \(N\) 表示所有可能的狀態的集合。

而連加符號的後面部分被定義為前向概率 \(\alpha_t(j)\)，而它可以被上一個時刻的前向概率迭代表示。

\[\begin{aligned}
\alpha_t(j) &=P(x_1,x_2,\ldots,x_t,s_t=j) \\ &= \sum_{i\in N} P(x_1,x_2,\ldots,x_{t-1},s_{t-1}=i)P(s_t|s_{t-1}=i)P(x_t|s_{t}=j) \\
&= \sum_{i\in N}\alpha_{t-1}(i) a_{ij} b_j(x_t)
\end{aligned}
\]

通過該方法，當前時刻下某個狀態的概率只需要遍歷上一時刻所有狀態的概率 (\(n\))，然後當前時刻的所有狀態的概率和也只需要遍歷當前的所有狀態就可以計算得到 (\(n\))，考慮到觀察序列持續了 \(T\) 個時刻，因此時間複雜度降為 \(O(n^2T)\)。

整個過程總結如下

  1. 初始化：根據初始的狀態分布，計算得到時刻1下每個狀態的前向概率 \(\alpha_1(k) = \pi_k b_k(x_1)\)
  2. 對於每個時刻，計算該時刻下每個狀態的前向概率 \(\alpha_t(j) = \sum_{i\in N}\alpha_{t-1}(i) a_{ij} b_j(x_t)\)
  3. 最終得到結果 \(P(X) = \sum_{i\in N}\alpha_{T}(i)\)

解碼問題

解碼問題就是說在得到 HMM 模型之後，我們如何通過觀察序列找到最有可能的狀態序列。在語音識別中，在給定的音頻片段下，找到對應的各個音素。

還是剛才的例子，我們需要猜測孩子讀出的這段聲音最有可能對應什麼樣的拼音序列，這就是解碼問題。

Viterbi 演算法

數學表示

給定在時間 \(t\) 下的內部狀態為 \(j\)，局部最優概率 \(v_t(j)\) 表示的是在時刻 \(t\) 觀察序列與最優內部狀態序列的聯合概率。

\[v_{t}(j)=\max _{s_{0}, s_{1} \ldots s_{t-1}} P\left(s_{0}, s_{1}, \ldots, s_{t-1}, x_{1}, x_{2}, \ldots, x_{t}, s_{t}=j | \theta\right)
\]

同樣也可以根據時間遞歸表示為

\[v_{t}(j)=\max_{i \in N} v_{t-1}(i) a_{i j} b_{j}\left(x_{t}\right)
\]

演算法具體流程如下

  1. 初始化：根據初始的狀態分布，計算得到時刻1下每個狀態的最優概率 \(v_1(k) = \pi_k b_k(x_1)\)
  2. 對於每個時刻，計算該時刻下每個狀態的局部最優概率 \(v_t(j) = \max_{i\in N}v_{t-1}(i) a_{ij} b_j(x_t)\)，記錄下最優局部最優序列 \((s_1^*,s_2^*,\ldots,s_{t-2}^*) \bigcup (s_{t-1}^*)\)
  3. 最終得到全局最優概率 \(P(X,S^*) = \max_{i\in N} v_T(i)\)
  4. 得到全局最優序列 \(S^* = \arg \max_{i\in N} v_T(i), S^* = (s_1^*,s_2^*,\ldots,s_T^*)\)

在表示上很類似於上面的前向演算法，只是加和變成了取最大值。具體推導流程也就不再贅述了。兩者的區別可以看下圖(來源) ，紅線表示解碼路徑，黑線表示評估路徑。

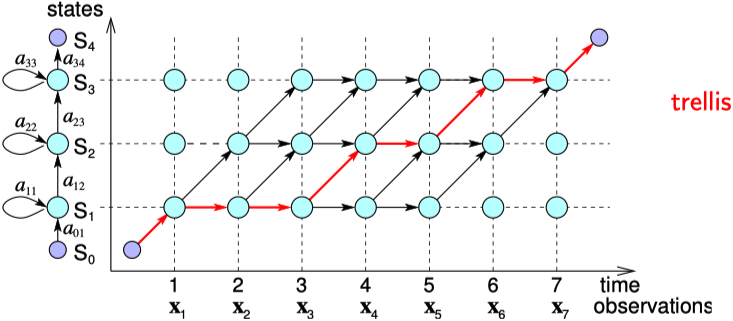
200627-HMM_Decode_path.png

不過這張圖是簡化的狀態，即狀態序列 \(S\) 是確定的情況下的狀態轉移與觀察序列之間的關係。

🤔思考：為何每次取局部最優最後就能得到全局最優？

這和一階馬爾可夫假設有關，因為每一個時刻的狀態只取決於上一個時刻的狀態，因此只要上一個時刻每一個狀態的前向概率是最大的，再乘上這一時刻對某個狀態的轉移概率和輸出概率，而這兩個概率在參數表裡是固定的，因此再選出乘出來的概率最大即可保證該時刻在這個時刻為這個狀態的概率最大，直到最後一個時刻。（類似於動態規劃的狀態轉移方程思想）

訓練問題

訓練 (learning) 問題主要是如何學習 HMM 模型參數(輸出概率和表現概率)的問題。在語音識別中，即在一開始只有音頻和標註的情況下，如何學習到模型。

還是剛剛那個例子，假如說你沒有教孩子，但給了他本語文教材和對應的錄音磁帶，他需要通過教材中的拼音和磁帶中的錄音來訓練語感 (比如說哪個拼音讀什麼音，每個拼音之後可能會跟什麼拼音)。他自學成才了以後我們才能做剛剛那兩個問題。

所以說訓練問題是評估和解碼問題的基礎，但是是三個問題中最複雜的，因為它是無閉式解的。

HMM 參數估計方法：

  • 最大似然 ：Baum-Welch 演算法
  • 貝葉斯：最大後驗
  • 判別訓練：MMI，MCE，MPE，sMBR

Baum–Welch 演算法

HMM訓練問題的標準演算法，又稱前向後向演算法，是 EM 演算法的特例。

後向演算法的表示和前向演算法類似，而後向概率 \(\beta_t(i)\) 表示的是在給定 \(t\) 時刻狀態為 \(i\)，看到時刻 t+1 到時刻 \(T\) 觀察序列的概率，表示為

\[\begin{aligned}
\beta_{t}(i) &= P(x_{t+1},x_{t+2},\ldots,x_{T}|s_{t} = i) \\
&= \sum_{j \in N} P(s_{t+1}=j | s_{t}=i) P(x_{t+1} | s_{t+1}=j) P(x_{t+1},x_{t+2},\ldots,x_{T}|s_{t+1} = j) \\
&= \sum_{j \in N} a_{ij}b_{t+1}(j)\beta_{t+1}(j) \\

\beta_{T}(i) &= 1 \\

\end{aligned}
\]

最後，整個觀察序列出現的概率用後向演算法表示為

\[P(X) = \sum_{j \in N} \pi_{j} b_{j}\left(x_{1}\right) \beta_{1}(j)
\]

為了能學習 HMM 模型參數，我們可以通過一個最大似然估計的變體評估我們的轉移概率 \(\hat{a}_{ij}\) ，可以表示為

\[\hat{a}_{ij} = \frac{從狀態i轉移到狀態j的期望次數}{從狀態i轉移到所有狀態的期望次數}
\]

但如何計算這些次數是個問題，假設我們可以估計在時刻 \(t\) 和給定觀察序列下從狀態 \(i\) 轉移到狀態 \(j\) 的概率，那我們就可以把每個時刻的概率加起來作為從狀態 \(i\) 轉移到狀態 \(j\) 的總次數。

我們定義了一個「狀態轉移佔有(occupation)率」 \(\xi_{t}(i,j)\) ，作為給定所有觀察序列的情況下在時刻 \(t\) 狀態為 \(i\) 後下一時刻轉移到狀態 \(j\) 的概率，表示為

\[\begin{aligned}
\xi_{t}(i,j) &=P\left(s_{t}=i, s_{t+1}=j | X, \theta\right) \\
&=\frac{P\left(s_{t}=i, s_{t+1}=j, X | \theta\right)}{P(X | \theta)}
\end{aligned}
\]

下圖(修改自來源)直觀地展示了 \(\xi_{t}(i,j)\) 分子部分的計算過程，因此其分子可以表示為 \(\alpha_{t}(i) a_{i j} \beta_{t+1}(j) b_{j}\left(x_{t+1}\right)\)

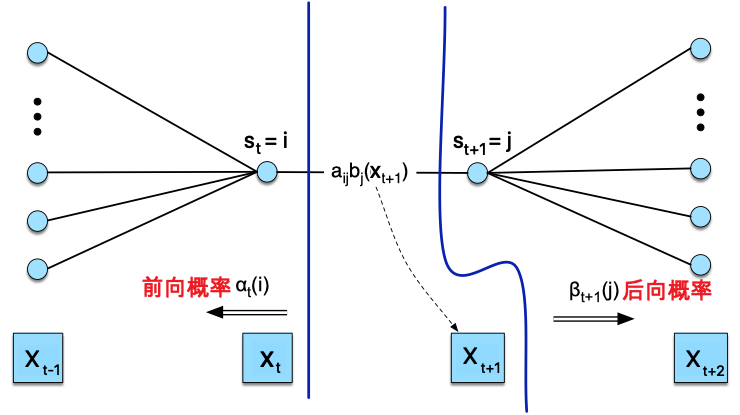
200628-HMM_State_transoccup_calc.png

而其分母部分則可以表示為某個時刻所有狀態的前向概率和後向概率的乘積和

\[\begin{aligned}
P(X | \theta) &= \sum_{k \in N}P(X_{1}^t, s_t=k | \theta)P(X_{t+1}^T | s_t = k, \theta)\\
& = \sum_{k\in N} \alpha_{t}(k) \beta_{t}(k)\\
\end{aligned}
\]

因此 \(\xi_{t}(i,j)\) 最後可表達為

\[\xi_{t}(i,j)=\frac{\alpha_{t}(i) a_{i j} \beta_{t+1}(j) b_{j}\left(x_{t+1}\right)}{\sum_{k\in N} \alpha_{t}(k) \beta_{t+1}(k)}
\]

我們可以把各個時刻的 \(\xi_{t}(i,j)\) 加起來作為「從狀態 \(i\) 轉移到狀態 \(j\) 的期望次數」，再將狀態 \(j\) 所有可能的狀態下的期望次數加和就可以得到「從狀態 \(i\) 轉移到所有狀態的期望次數」，從而計算得到 \(\hat{a}_{ij}\)。

\[\hat{a}_{i j}=\frac{\sum_{t=1}^{T-1} \xi_{t}(i,j)}{\sum_{t=1}^{T-1} \sum_{j \in N}\xi_{t}(i,j)}
\]

我們同樣需要一個用於計算輸出概率 \(\hat{b}_j(v_k)\) 的最大似然估計公式，\(v_k\) 表示的是輸出序列中的第 \(k\) 個音素對應的音頻特徵。

\[\hat{b}_j(x_t) = \frac{在狀態j下觀察到v_k的期望次數}{在狀態j下所有的期望觀察次數}
\]

為了計算這個公式，我們需要知道在給定觀察序列的情況下在時刻 \(t\) 的狀態為 \(i\) 的概率，我們將其稱為「狀態佔有率」 \(\gamma_{t}(i)\),

\[\begin{aligned}
\gamma_{t}(i) &=P\left(s_{t}=i | X, \theta\right)\\
&= \frac{P\left(s_{t}=i, X | \theta\right)}{P(X | \theta)} \\
\end{aligned}
\]

而分子部分的概率其實剛剛我們在計算 \(\xi_{t}(i,j)\) 分母時已經用到了，即時刻 \(t\) 下為狀態 \(i\) 的前向概率乘上後向概率。

\[\begin{aligned}
\gamma_{t}(i)
&= \frac{P(X_{1}^t, s_t=i | \theta)P(X_{t+1}^T | s_t = i, \theta)}{p(X | \theta)}\\
&=\frac{\alpha_{t}(i) \beta_{t}(i)}{\sum_{k\in N} \alpha_{t}(k) \beta_{t}(k)}
\end{aligned}
\]

得到了 \(\gamma_{t}(i)\) 以後，就可以用他來計算 \(\hat{b}_j(v_k)\) 了，我們加上了所有 \(x_t\) 為 \(v_k\) 的 時刻的 \(\gamma_{t}(i)\) 作為分子，而分母就是所有時刻的 \(\gamma_{t}(i)\) 之和。

\[\hat{b}_{i}\left(v_k\right)=\frac{\sum_{t=1,s.t. x_t=v_k}^{T} \gamma_{t}(i)}{\sum_{t=1}^{T} \gamma_{t}(i)}
\]

同時，\(\hat{a}_{ij}\) 的分母也可以用 \(\gamma_{t}(i)\) 來表示

\[\hat{a}_{i j}=\frac{\sum_{t=1}^{T-1} \xi_{t}(i,j)}{\sum_{t=1}^{T-1} \gamma_{t}(i)}
\]

得到新的 HMM 參數 \(\theta_1\) 後，又可以計算得到新的 \(\theta_2\)，同樣又可以估計得到新的最佳 \(\theta_1\)，一直迭代這個過程直到收斂。

在 E 步建立 \(P(\gamma,\xi | x, a, b)\)，然後 M 步 找到將上式最大化的參數 \(a, b\)，具體流程如下

  1. 初始化：初始化轉移概率矩陣 \(A\)，以及輸出概率矩陣 \(B\)
  2. E 步：
    1. 計算得到每個時刻的每個狀態的前向概率 \(\alpha_t(i)\) 和後向概率 \(\beta_t(i)\)
    2. 更新狀態佔有率 \(\gamma_{t}(i)\) 和 狀態轉移佔有率 $$\xi_{t}(i,j)$$
  3. M 步：
    1. 計算得到期望概率：
      1. 期望初始化概率 \(\hat{\pi}_{i}=\gamma_{1}(i)\)
      2. 期望轉移概率 \(\hat{a}_{ij}\)
      3. 期望輸出概率 \(\hat{b}_j(v_k)\)
  4. 不停迭代 E 步 M 步 直到收斂

儘管從原理上來講前向後退演算法可以完全無監督地學習參數，但實際上初始化非常重要。 因此，通常會給演算法額外的資訊。 例如，對於基於 HMM 的語音識別，通常手動設定 HMM 結構，並且從一組觀察序列 \(X\) 中僅訓練輸出概率和(非零的)轉移概率。

GMM

高斯混合模型 (Gaussian mixture model，GMM) 就是用混合的高斯隨機變數的分布來擬合訓練數據（音頻特徵）形成的模型。該方法提供了一種基於規則的方法來衡量一個音素和被觀察音頻幀的「距離」。

給定一個音素，我們可以使用 GMM 學習觀察值的特徵向量，這個概率分布允許我們在給定一個音素(狀態)下計算音頻段的似然 \(P(x | s)\).

單變數高斯分布

假設觀察向量中某個特徵 \(x\) 的分布為正態分布，那麼該特徵 \(x\) 的似然函數可以表示為均值為 \(\mu\) 方差為 \(\sigma^2\) 的高斯分布

\[f(x|\mu,\sigma)=\mathcal{N}\left(\mu, \sigma^{2}\right)=\frac{1}{\sigma \sqrt{2 \pi} } e^{-\frac{(x-\mu)^{2}}{2 \sigma^{2}}}
\]

在被標記了狀態的訓練數據下，我們可以計算的到關於狀態 \(i\) 的均值和方差

\[\begin{array}{l}
\mu_{i}=\frac{1}{T} \sum_{t=1}^{T} x_{t} & \text { s.t. } x_{t} \text { is state } i \\
\sigma_{i}^{2}=\frac{1}{T} \sum_{t=1}^{T}\left(x_{t}-\mu_{i}\right)^{2} & \text{ s.t. } q_{t} \text { is state } i
\end{array}
\]

高斯分布易於從訓練數據中學習並且讓我們有了一個良好的似然函數 \(f(x|\mu,\sigma)\)。在語音識別中我們可以為每個音素(狀態)學到一個高斯分布，這將作為似然概率，也可以作為 HMM 中的輸出概率。

根據 HMM 在時刻 \(t\) 下所處狀態 \(i\) 的概率，將每個觀察向量 \(x_t\) 按比例分配給每個可能的狀態 \(i\)。而在時刻 \(t\) 處於狀態 \(i\) 的概率在 HMM 中為表示為狀態佔有率 \(\gamma_t(i)\)，因此可以在將高斯分布的參數期望表示為

\[\bar{\mu}_{i}=\frac{\sum_{t=1}^{T} \gamma_{t}(i) x_{t}}{\sum_{t=1}^{T} \gamma_{t}(i)} \quad \bar{\sigma}_{i}^{2}=\frac{\sum_{t=1}^{T} \gamma_{t}(i)\left(x_{t}-\mu_{i}\right)^{2}}{\sum_{t=1}^{T} \gamma_{t}(i)}
\]

多變數高斯分布

在多變數高斯分布中，我們將均值 \(\mu\) 替換為多個特徵均值的向量 \(\boldsymbol{\mu} = \left(\mu_1,\ldots,\mu_n\right)^T\)，將方差 \(\sigma\) 替換為協方差矩陣 \(\Sigma\in\mathbb{R}^{n\times n}\)，其中第 \(i\) 行 \(j\) 列個元素表示為 \(\sigma_{ij}^2 = E\left[(x_i-\mu_i)(x_j-\mu_j)\right]\)，最終的高斯分布表示為

\[f(x | \boldsymbol{\mu}, \Sigma)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} e^{-\frac{1}{2}(x-\boldsymbol{\mu})^{T} \Sigma^{-1}(x-\boldsymbol{\mu})}
\]

通過快速傅立葉變化 FFT 得到的特徵之間是相關的，但通過梅爾倒譜相關係數 MFCC 得到的特徵之間是不相關的。在特徵不相關的情況下，協方差矩陣是對角陣，計算和存儲代價小了很多。這樣我們就可以單獨考慮每個聲學特徵的方差。

混合高斯分布

但單個高斯分布可能並不能很好地來對特徵的分布進行建模 (現實世界總是沒有那麼理想化)，因此採用多個加權的高斯分布來對對特徵分布建模。

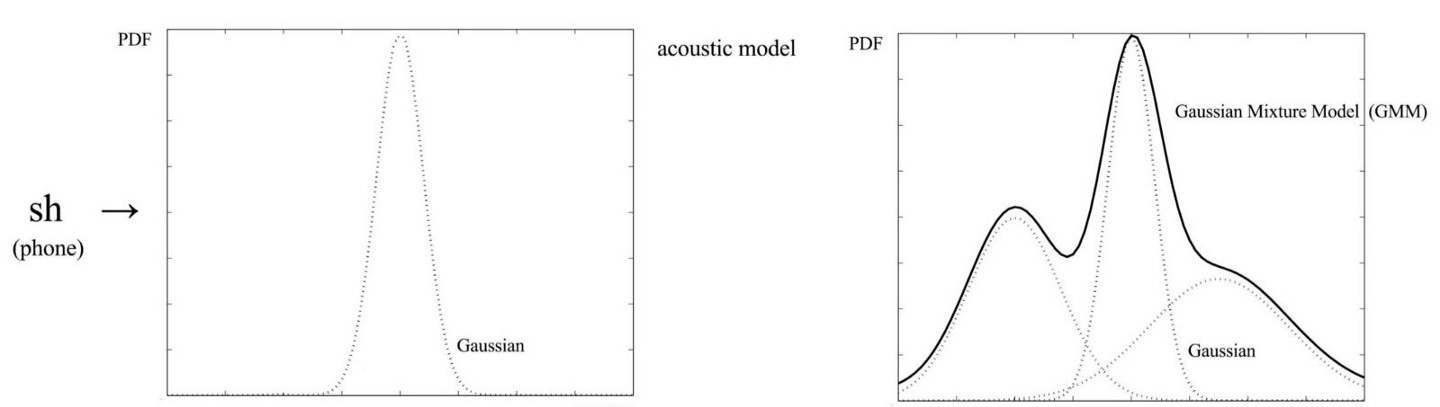
200628-GMM_distribution.jpg

比如說上圖(來源)中的3分量 GMM，有6個高斯參數加上3個權重。

因此，對於一個 HMM 的狀態 \(j\)，觀察特徵向量 \(x\) 的似然函數可以表示為

\[b_{j}(x)=p(x | s=j)=\sum_{m=1}^{M} c_{j m} \mathcal{N}\left(x ; \boldsymbol{\mu}_{j m}, \Sigma_{j m}\right)
\]

其中 M 為 GMM 的分量數，而 \(c_{j m}\) 表示的是在狀態 \(j\) 下第 \(m\) 個分量的權重。

在實際的 GMM 訓練中，通常採用 EM 演算法來進行迭代優化，以求取 GMM 中的加權係數及各個高斯函數的均值與方差等參數。

缺點：

  • 不能考慮語音的順序資訊
  • 高斯混合分布也很難擬合非線性或者近似非線性的數據特徵

最後再重聲一下，GMM 用於對音素所對應的音頻特徵分布進行建模，而 HMM 則用於音素轉移和音素對應輸出音頻特徵之間關係的建模。

寫不動了，HMM 和 GMM 梳理推導了好久，如果各位讀者有不懂的歡迎留言討論～👏

參考鏈接：

Tags:

VirMach 便宜 VPS

QNews

QNews