三角函數與緩入緩齣動畫及C#實現(圖文講解)
日常經常能看到緩入緩出的動畫效果,如:
1,帶緩入緩出效果的滾動條:

2,帶緩入緩出效果的呼吸燈:

像上面這種效果,就是用到了三角函數相關的知識,下面將從頭開始一步步去講解如何實現這種效果。
一、基礎知識
(一)三角函數
常用的三角函數有正弦函數(sin)、餘弦函數(cos)、正切函數(tan)。在動畫效果中常用的是正弦函數和餘弦函數,由於兩者可以互相轉化,所以本文將以正弦函數來進行講解。
如下圖所示直角三角形ABC:
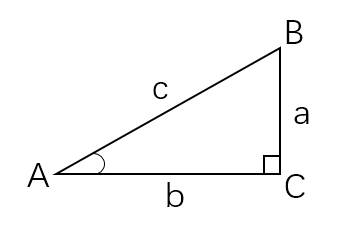
則:
sin(A)=a/c
即:角A的正弦值=角A的對邊/斜邊
(二)正弦曲線
將三角函數與動畫橋接起來的便是三角函數曲線。
以正弦函數為例,其正弦曲線公式為:y = A*sin(B*x + C) + D
其中y、x分別是縱坐標、橫坐標。
1,在默認狀態時,即:y=sin(x) 時,其曲線如下圖所示:
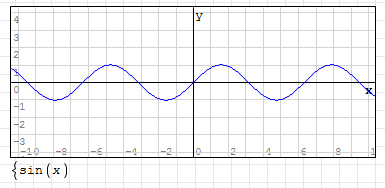
2,正弦曲線公式中的參數 「A」 控制曲線的振幅,A 值越大,振幅越大,A 值越小,振幅越小。
如:y=2*sin(x),其曲線如下圖所示(藍線為 y=sin(x)):
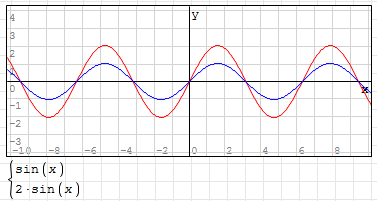
3,參數 「B” 控控制曲線的周期,B 值越大,那麼周期越短,B 值越小,周期越長。
如:y=sin(2x),其曲線如下圖所示(藍線為 y=sin(x)):
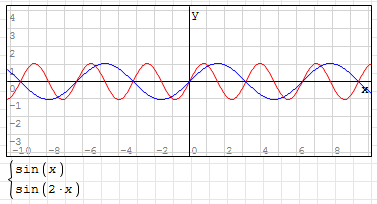
4,參數 「C” 控控制曲線左右移動,C 值為正數,曲線左移,C 值為負數,曲線右移;
如:y=sin(x+1),其曲線如下圖所示(藍線為 y=sin(x)):
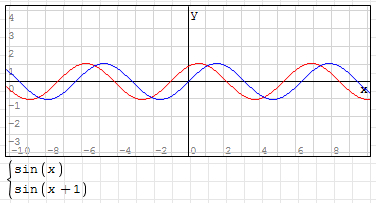
5,參數 「D” 控控制曲線上下移動。D 值為正數,曲線上移,D 值為負數,曲線下移;
如:y=sin(x)+1,其曲線如下圖所示(藍線為 y=sin(x)):

(三)角度與弧度
因為在使用程式碼去計算正弦值時,其單位一般是弧度,像C#中的」Math.Sin()「函數,而直觀的效果卻是角度,所以需要講解一下角度與弧度。
1,角度
定義:兩條射線從圓心向圓周射出,形成一個夾角和夾角正對的一段弧。當這段弧長正好等於圓周長的360分之中的一個時,兩條射線的夾角的大小為1度。
示意圖如下:

2,弧度
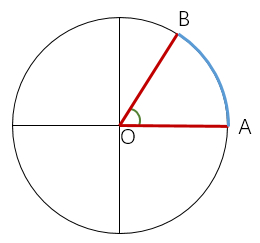
定義:弧度:兩條射線從圓心向圓周射出,形成一個夾角和夾角正對的一段弧。當這段弧長正好等於圓的半徑時,兩條射線的夾角大小為1弧度。
示意圖如下:
其中:AB=OA=r
3,角度與弧度的差別
最基本的差別在於角所對的弧長大小不同。度的是等於圓周長的360分之中的一個,而弧度的是等於半徑。
4,角度與弧度的轉換
因為:弧度角=弧長/半徑
所以:
a,周角(360度)=周長/半徑=2πr/r=2π
b,平角(180度)=π
由b可知:180度=π弧度
所以:
c,1度=π/180 弧度(≈0.017453弧度)
d,1弧度=180/π 度(≈57.3度)
可得轉換公式:
弧度=度*π/180
度=弧度*180/π
三、動畫實現
實現的思路簡單而言便是利用正弦曲線的」y「和」x「值的變化。對於緩入緩齣動畫,就是速度的變化。
速度的定義和公式:速度在數值上等於物體運動的位移跟發生這段位移所用的時間的比值。速度的計算公式為v=Δs/Δt
控制速度,無非是」距離「與」時間「這兩個量的變化。
在實現應用中,往往不會同時變化兩個量,而是固定一個量,變化一個量。
在實際程式實現時,一般是固定「時間」,只變化「距離」。此處的」時間「可以理解為」時間間隔「。即在時間間隔不變的情況下,需要考慮每個時間間隔內運行的距離。
那麼在正弦曲線上的體現便是等x間隔下,y的取值。
(一)簡單實現
(1)實現思路:
1,通過y=sin(x)的曲線可知:y值的範圍是(-1~+1)
2,將曲線上移,上移距離為1,即:y=sin(x)+1,此時y值的範圍:(0~2)
3,為使y值範圍變為(0~1),對函數除2,即:y=(sin(x)+1)/2
如圖(藍線為 y=sin(x)):
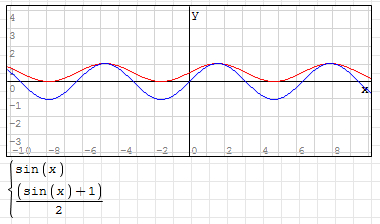
4,將y值乘以緩入緩齣動畫的擺動距離
(2)C#實現:
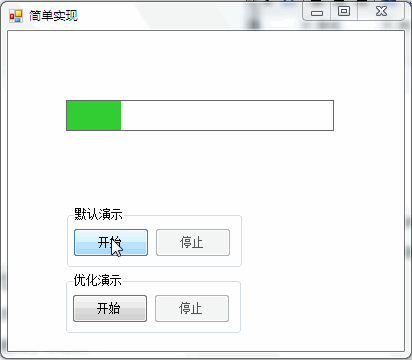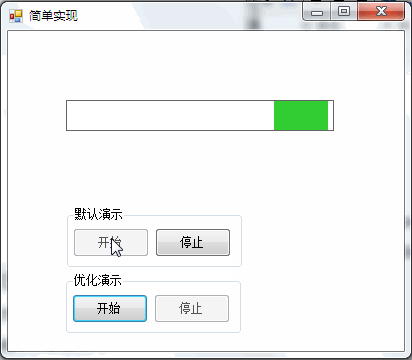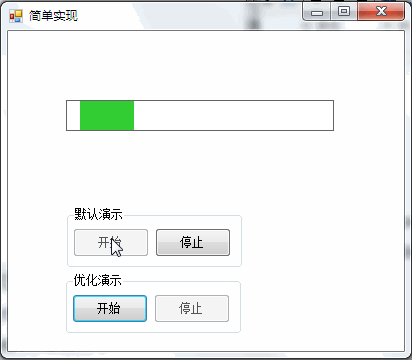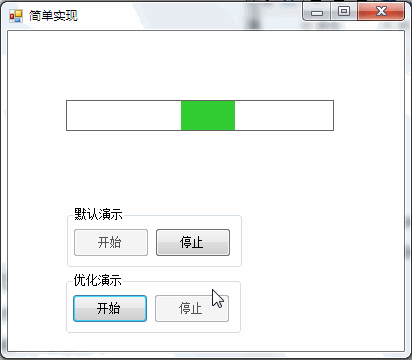
1,控制項布局及屬性

2,核心程式碼


1 void pShowD() 2 { 3 //i是度數,不是弧度 4 int i = 0; 5 //移動距離要減去滑塊本身的寬度 6 double dMoveDistance = panel_Board.Width - panel_Slider.Width; 7 while (true) 8 { 9 i++; 10 if (i > 360) 11 { 12 //一個周期是360度 13 i = 0; 14 } 15 //固定時間間隔 16 Thread.Sleep(10); 17 //通過公式:弧度=度*π/180,將度數i轉為Math.Sin()所需要的弧度數 18 double dz = dMoveDistance * (1 + Math.Sin(i * Math.PI / 180)) / 2; 19 pSetLeft(Convert.ToInt32(dz)); 20 21 } 22 } 23 24 void pSetLeft(int i) 25 { 26 if (panel_Slider.InvokeRequired) 27 { 28 panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i }); 29 } 30 else 31 { 32 panel_Slider.Left = i; 33 } 34 }
簡單實現
3,運行效果
(二)簡單實現優化
通過觀察上面的實現,可以發現雖然實現了緩入緩出效果,但是其」滑塊「(panel_Slider)的起始位置卻不是最左側,而是從中間開始。
根據上面的公式也可以看出來,當x=0時,y=(sin(x)+1)/2=1/2,即:整個擺動距離的二分之一。
(1)優化思路
為了讓滑塊從最左側開始,則需要將曲線向右移動,移動距離是π/2。
其曲線公式變為:y=(sin(x-π/2)+1)/2
如圖(藍線為 y=sin(x)):
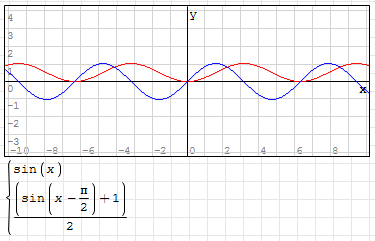
(2)C#實現
1,布局同上。
2,核心程式碼


1 void pShowD2() 2 { 3 //i是度數,不是弧度 4 int i = 0; 5 //移動距離要減去滑塊本身的寬度 6 double dMoveDistance = panel_Board.Width - panel_Slider.Width; 7 while (true) 8 { 9 i++; 10 if (i > 360) 11 { 12 //一個周期是360度 13 i = 0; 14 } 15 //固定時間間隔 16 Thread.Sleep(10); 17 //通過公式:弧度=度*π/180,將度數i轉為Math.Sin()所需要的弧度數 18 //因為i是度數,所以是(i-90) 19 double dz = dMoveDistance * (1 + Math.Sin((i-90) * Math.PI / 180)) / 2; 20 pSetLeft(Convert.ToInt32(dz)); 21 22 } 23 } 24 25 void pSetLeft(int i) 26 { 27 if (panel_Slider.InvokeRequired) 28 { 29 panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i }); 30 } 31 else 32 { 33 panel_Slider.Left = i; 34 } 35 }
簡單實現(優化)
3,運行效果

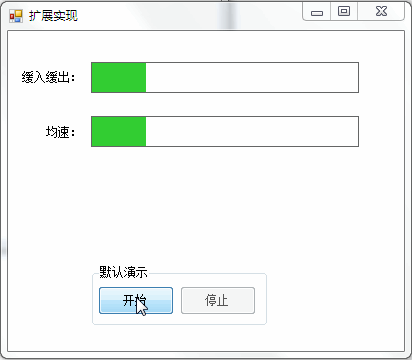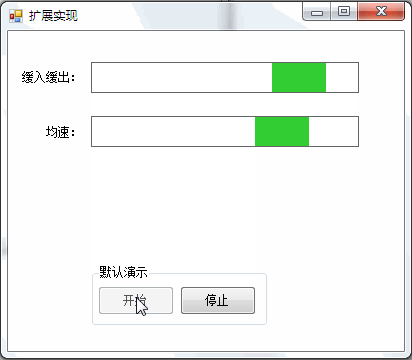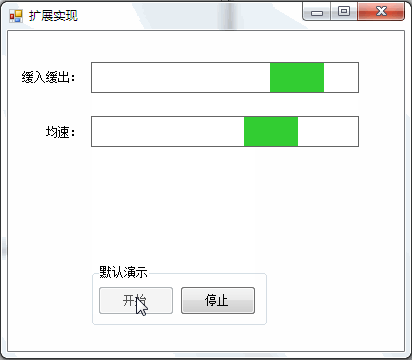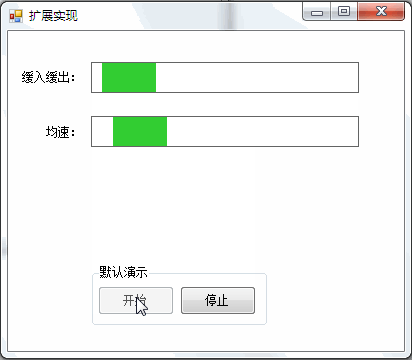
(三)擴展實現
在實際應用中,動畫往往需要在」固定時間「內完成。
以前面實現為例,使滑塊從左端滑到右端的時長固定為1秒。該怎麼實現呢?
(1)實現思路
整體思路與之前的並沒有什麼大的區別,仍是固定」時間「,變化」距離「。
在前面的」簡單實現(優化)「的基礎上,需要增加下面的一些修改和補充:
1,假設」時間間隔「為:Interval,那麼,在指定的1秒內,共會變化(Step=1/Interval)次。
2,那麼,每次變化時度數的變化便不再是」1「,又一個周期是滑塊一個來回,所以,第次變化的度數便是:Per=2π/2*Step=180/Step。
(2)C#實現
在實現時加入了勻速的對比。
1,布局及屬性
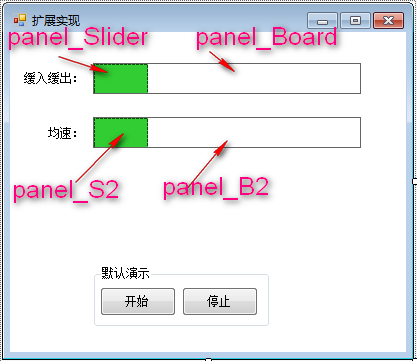
2,核心程式碼


1 void pShowD2() 2 { 3 //當前滑塊的位置 4 double d = 0; 5 //true/false:向右滑/向左滑 6 bool bToRight = true; 7 //時間間隔,單位:ms 8 int iInterval = 10; 9 //從左到右所需要的總時間,單位:ms 10 int iAnimateTime = 1000; 11 //移動距離要減去滑塊本身的寬度 12 double dMoveDistance = panel_Board.Width - panel_Slider.Width; 13 //需要變化的次數 14 double dStep = Convert.ToDouble(iAnimateTime) / iInterval; 15 //每次變化所增加的距離 16 double dPerX = dMoveDistance / dStep; 17 while (true) 18 { 19 d = bToRight ? d + dPerX : d - dPerX; 20 if (d > dMoveDistance) 21 { 22 bToRight = false; 23 } 24 if (d < 0) 25 { 26 bToRight = true; 27 } 28 29 Thread.Sleep(iInterval); 30 int iZ = Convert.ToInt32(d); 31 pSetLeft2(iZ); 32 33 } 34 } 35 void pSetLeft2(int i) 36 { 37 if (panel_S2.InvokeRequired) 38 { 39 panel_S2.Invoke(new Action<int>(pSetLeft2), new object[] { i }); 40 } 41 else 42 { 43 panel_S2.Left = i; 44 } 45 }
1,勻速


1 void pShowD() 2 { 3 //d是度數,不是弧度 4 double d = 0; 5 //時間間隔,單位:ms 6 int iInterval = 10; 7 //從左到右所需要的總時間,單位:ms 8 int iAnimateTime = 1000; 9 //移動距離要減去滑塊本身的寬度 10 double dMoveDistance = panel_Board.Width - panel_Slider.Width; 11 //需要變化的次數 12 double dStep = Convert.ToDouble(iAnimateTime) / iInterval; 13 //每次變化所增加的度數 14 double dPer = 180.0 / dStep; 15 while (true) 16 { 17 d += dPer; 18 if (d > 360) 19 { 20 //一個周期是360度 21 d = 0; 22 } 23 //固定時間間隔 24 Thread.Sleep(iInterval); 25 //通過公式:弧度=度*π/180,將度數i轉為Math.Sin()所需要的弧度數 26 double dz = dMoveDistance * (1 + Math.Sin((d - 90) * Math.PI / 180)) / 2; 27 pSetLeft(Convert.ToInt32(dz)); 28 29 } 30 } 31 32 void pSetLeft(int i) 33 { 34 if (panel_Slider.InvokeRequired) 35 { 36 panel_Slider.Invoke(new Action<int>(pSetLeft), new object[] { i }); 37 } 38 else 39 { 40 panel_Slider.Left = i; 41 } 42 }
2,緩入緩出
3,運行效果
四、結束語
本篇主要講的是三角函數與緩入緩齣動畫,但三角函數在動畫中的作用不僅僅如此,比如直接使用正弦曲線的形狀來繪製波浪效果——在充電、進度條等地方可以使用該效果。
而且即然知道在曲線在動畫中的作用,那麼便可以通過不同的函數曲線實現不同的動畫效果,比如另一個非常好用的」貝塞爾曲線「,可以實現更複雜、更優雅的動畫效果。
如有錯誤和不足之處歡迎大家批評指正。


