Kalman Filter、Extended Kalman Filter以及Unscented Kalman Filter介紹

2019 年 10 月 3 日
筆記

模型定義

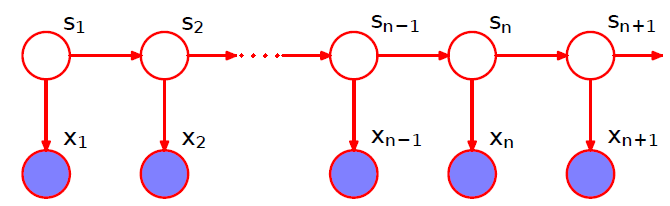
如上圖所示，卡爾曼濾波(Kalman Filter)的基本模型和隱馬爾可夫模型類似，不同的是隱馬爾科夫模型考慮離散的狀態空間，而卡爾曼濾波的狀態空間以及觀測空間都是連續的，並且都屬於高斯分布，因此卡爾曼濾波又稱為linear Gaussian Markov model，它的數學定義如下：$$underbrace{s_{t}=C s_{t-1}+G h_{t}+gamma_{t}}_{text { latent process }}, quad underbrace{x_{t}=D s_{t}+varepsilon_{t}}_{text { observed process }}$$其中$h_t$表示控制向量(control vector)，是已知量；$gamma_{t} sim N(0, Q)$表示狀態誤差，它包含了狀態轉換公式$C s_{t-1}+G h_{t}$中未考慮到的其它因素，是狀態轉換公式準確性的度量；$varepsilon_{t} sim N(0, V)$表示觀測誤差，是觀測精度的度量。下面舉一個簡單的例子：

假設有一個二維空間上的物體位置的觀測序列($x_{t} in mathbb{R}^{2}$)，觀測有一定誤差；該物體的狀態$s_t=[p_{t1},v_{t1},p_{t2},v_{t2}]^T$，其中$p_t$和$v_t$表示物體位置和速度，下標1和2表示方向；控制向量為$h_t=[a_{t1},a_{t2}]^T$，$a_t$表示加速度。由基本的物理公式可知$$s_{t}=underbrace{left[begin{array}{cccc}{1} & {Delta t} & {0} & {0} \ {0} & {1} & {0} & {0} \ {0} & {0} & {1} & {Delta t} \ {0} & {0} & {0} & {1}end{array}right]}_{C}s_{t-1}+underbrace{left[begin{array}{cc} frac{1}{2}(Delta t)^{2} & {0} \ {Delta t} & {0} \ {0} & frac{1}{2}(Delta t)^{2} \ {0} & {Delta t}end{array}right]}_{G}h_t+gamma_ttext{ 以及 }x_{t}=underbrace{left[begin{array}{cccc}{1} & {0} & {0} & {0} \ {0} & {0} & {1} & {0}end{array}right]}_{D}s_{t}+varepsilon_{t}$$

卡爾曼濾波的目標是已知觀測序列$x_1,x_2,cdots,x_t$，計算當前隱藏狀態的分布函數，即$$s_{t}left|s_{t-1} sim Nleft(C s_{t-1}+G h_{t}, Qright), quad x_{t}right| s_{t} sim Nleft(D s_{t}, Vright)quad
Rightarrowquad pleft(s_{t} | x_{1}, dots, x_{t}right);quad 1leq t leq T$$注意除觀測序列以外，矩陣$C,G,Q,D,V$以及控制向量$h_t$也是給定的。

模型求解

定義$S_t=(s_{t} | x_{1}, ldots, x_{t})$，容易看出$S_t$滿足高斯分布$N(mu_{t}, Sigma_{t})$，$mu_t$以及$Sigma_t$即為需要求解的量
- 為方便之後的計算，令$S_{t-1}=(s_{t-1} | x_{1}, ldots, x_{t-1})=underbrace{mu_{t-1}}_text{mean}+Delta S_{t-1},quad Delta S_{t-1} sim N(0,Sigma_{t-1})$
定義$P_t= (s_{t} | x_{1}, ldots, x_{t-1})$，有$P_t=CS_{t-1}+G h_{t}+gamma_{t}$
- 為方便之後的計算，令$P_t=underbrace{Cmu_{t-1}+Gh_t}_{mu_{P_t}}+underbrace{CDelta S_{t-1}+gamma_t}_{Delta P_t}$
定義$O_t= (x_{t} | x_{1}, ldots, x_{t-1})$，有$O_t=DP_{t}+varepsilon_t$
- 為方便之後的計算，令$O_t=underbrace{D(Cmu_{t-1}+Gh_t)}_{mu_{O_t}}+underbrace{DCDelta S_{t-1}+Dgamma_t+varepsilon_t}_{Delta O_t}$

由上述定義可知 $$left[begin{array}{c} P_t \ O_t end{array}right] sim Nleft(left[begin{array}{c} mu_{P_t} \ mu_{O_t} end{array}right], left[begin{array}{cc} Sigma_{PP} & Sigma_{PO}\ Sigma_{PO}^T & Sigma_{OO} end{array}right] right)$$接下來計算協方差矩陣的這些項：

$Sigma_{PP}=mathbb{E}[{Delta P_t (Delta P_t)^T}]=Cmathbb{E}[Delta S_{t-1} (Delta S_{t-1})^T]C^T+mathbb{E}[gamma_tgamma_t^T]=CSigma_{t-1}C^T+Q$
$Sigma_{PO}=mathbb{E}[{Delta P_t (Delta O_t)^T}]=Cmathbb{E}[Delta S_{t-1} (Delta S_{t-1})^T]C^TD^T+mathbb{E}[gamma_tgamma_t^T]D^T=CSigma_{t-1}C^TD^T+QD^T$
$Sigma_{OO}=mathbb{E}[{Delta O_t (Delta O_t)^T}]=DCmathbb{E}[Delta S_{t-1} (Delta S_{t-1})^T]C^TD^T+Dmathbb{E}[gamma_tgamma_t^T]D^T+mathbb{E}[varepsilon_tvarepsilon_t^T]=DCSigma_{t-1}C^TD^T+DQD^T+V$

容易看出$S_t=(P_t | O_t)$，此外定義$$hat{mu}_t=mu_{P_t}=C mu_{t-1}+Gh_t，text{ }hat{Sigma}_t=Sigma_{PP}=C Sigma_{t-1} C^{T}+Qtext{以及卡爾曼增益矩陣}K_t=hat{Sigma}_{t}D^T[Dhat{Sigma}_{t}D^T+V]^{-1}$$由高斯分布的性質可知

$Sigma_t=Sigma_{PP}-Sigma_{PO}Sigma_{OO}^{-1}Sigma_{PO}^T=(I-K_tD)hat{Sigma}_t$
$mu_t=mu_{P_t}+Sigma_{PO}Sigma_{OO}^{-1}(O_t-mu_{O_t})=hat{mu}_t+K_t(x_t-Dhat{mu}_t)$

上述求解過程可歸納為：

初始化$mu_0$以及$Sigma_0$
預測：$hat{mu}_t=C mu_{t-1}+Gh_t$以及$hat{Sigma}_t=C Sigma_{t-1} C^{T}+Q$
計算卡爾曼增益矩陣$K_t=hat{Sigma}_{t}D^T[Dhat{Sigma}_{t}D^T+V]^{-1}$
更新：$mu_t=hat{mu}_t+K_t(x_t-Dhat{mu}_t)$以及$Sigma_t=(I-K_tD)hat{Sigma}_t$

Extended Kalman Filter

在Extended Kalman Filter中，狀態之間的轉化以及狀態向觀測的轉化是非線性的，即$$s_t=g(s_{t-1},h_t)+gamma_t,text{ }x_{t}=f(s_{t})+varepsilon_{t};text{ 其中}g,ftext{代表非線性函數}$$此時考慮使用泰勒公式將非線性函數近似為線性函數，延續上一部分的定義，有

$P_t=g(S_{t-1},h_t)+gamma_{t}=g(mu_{t-1}+delta S_{t-1},h_t)+gamma_{t}=underbrace{g(mu_{t-1},h_t)}_{mu_{P_t}(text{i.e., }hat{mu}_t)}+underbrace{J_gDelta S_{t-1}+gamma_{t}}_{Delta P_t}$
$O_t=h(P_t)+varepsilon_t=f(mu_{P_t}+Delta P_t)+varepsilon_t=f(mu_{P_t})+J_fDelta P_t+varepsilon_t=underbrace{f(hat{mu}_{t})}_{mu_{O_t}}+underbrace{J_fJ_gDelta S_{t-1}+J_fgamma_t+varepsilon_t}_{Delta O_t}$

其中$J_g$和$J_f$為Jacobian矩陣，假設狀態為$m$維向量，觀測為$n$維向量，並且$g(s,h)=[g_1(s,h),cdots,g_m(s,h)]^T$以及$f(s)=[f_1(s),cdots,f_n(s)]^T$，則有$$J_g=left[begin{array}{cccc}frac{partial g_1}{partial mu_{t-1,1}} & frac{partial mu_1}{partial s_{t-1,2}} & cdots & frac{partial g_1}{partial mu_{t-1,m}} \ vdots & vdots & vdots & vdots \ frac{partial g_m}{partial mu_{t-1,1}} & frac{partial g_m}{partial mu_{t-1,2}} & cdots & frac{partial g_m}{partial mu_{t-1,m}}end{array}right], text{ }J_f=left[begin{array}{cccc}frac{partial f_1}{partial hat{mu}_{t,1}} & frac{partial f_1}{partial hat{mu}_{t,2}} & cdots & frac{partial f_1}{partial hat{mu}_{t,m}} \ vdots & vdots & vdots & vdots \ frac{partial f_n}{partial hat{mu}_{t,1}} & frac{partial f_n}{partial hat{mu}_{t,2}} & cdots & frac{partial f_n}{partial hat{mu}_{t,m}}end{array}right]$$容易看出Extended Kalman Filter的求解過程可歸納為：

初始化$mu_0$以及$Sigma_0$
預測：$hat{mu}_t=g(mu_{t-1},h_t)$以及$hat{Sigma}_t=J_g Sigma_{t-1} J_g^{T}+Q$
計算卡爾曼增益矩陣$K_t=hat{Sigma}_{t}J_f^T[J_fhat{Sigma}_{t}J_f^T+V]^{-1}$
更新：$mu_t=hat{mu}_t+K_t[x_t-f(hat{mu}_t)]$以及$Sigma_t=(I-K_tJ_f)hat{Sigma}_t$

Unscented Kalman Filter

Unscented Kalman Filter和Extended Kalman Filter的模型定義一樣，只是具體求解方法不同。相對於Extended Kalman Filter使用泰勒公式近似非線性函數，Unscented Kalman Filter通過選取多個樣本點(the sigma points)直接估計均值和方差。仍然延續之前的定義，假設狀態為$m$維向量，從隨機變數$S_{t-1}$中選取$2m+1$個樣本點，記為矩陣$mathcal{X}_{t-1}$($m$行$2m+1$列)，選取方式為$$mathcal{X}_{t-1}=left[begin{array}{ccc}mu_{t-1} & mu_{t-1}+sqrt{(m+lambda )Sigma_{t-1}} & mu_{t-1}-sqrt{(m+lambda )Sigma_{t-1}} end{array}right]$$若將$Sigma_{t-1}$進行Cholesky分解得到$LL^T$，則$sqrt{Sigma_{t-1}}=L$；或者對$Sigma_{t-1}$進行特徵值分解得到$ULambda U^T$(其中$Lambda$為對角陣)，則$sqrt{Sigma_{t-1}}=ULambda^{1/2}$。接下來對每個取樣點分配權重：

$vec{w}_a=left[begin{array}{ccccc}frac{lambda}{m+lambda} & frac{1}{2(m+lambda)} & frac{1}{2(m+lambda)} & cdots & frac{1}{2(m+lambda)}end{array}right]$
$vec{w}_c=left[begin{array}{ccccc}frac{lambda}{m+lambda}+(1-alpha^2+beta) & frac{1}{2(m+lambda)} & frac{1}{2(m+lambda)} & cdots & frac{1}{2(m+lambda)}end{array}right]$

其中$vec{w}_a$為求均值時的權重，$vec{w}_c$為求協方差矩陣時的權重。針對一些參數的取值有以下建議：$$alpha in (0,1],text{ }beta=2,text{ }lambda=alpha^2(m+kappa)-m,text{ }kappageq 0$$將$mathcal{X}_{t-1}$代入函數$g$可以得到$$hat{mathcal{X}}_{t}=left[begin{array}{cccc}g(mathcal{X}_{t-1}^{[1]},h_t) & g(mathcal{X}_{t-1}^{[2]},h_t) & cdots & g(mathcal{X}_{t-1}^{[2m+1]},h_t)end{array}right]$$其中上標表示矩陣的列數，由$hat{mathcal{X}}_{t}$可以估計出$hat{mu}_t$以及$hat{Sigma}_t$，接下來可以通過兩種方式得到觀測的取樣點$mathcal{Z}_t$：

直接通過$hat{mathcal{X}}_{t}$進行計算，即$$mathcal{Z}_{t}=left[begin{array}{cccc}h(hat{mathcal{X}}_{t}^{[1]}) & h(hat{mathcal{X}}_{t}^{[2]}) & cdots & h(hat{mathcal{X}}_{t}^{[2m+1]}) end{array}right]$$
通過得到的$hat{mu}_t$以及$hat{Sigma}_t$重新取樣，有公式$$hat{mathcal{X}}_{t}^*=left[begin{array}{ccc}hat{mu}_{t} & hat{mu}_{t}+sqrt{(m+lambda )hat{Sigma}_{t}} & hat{mu}_{t}-sqrt{(m+lambda )hat{Sigma}_{t}} end{array}right]$$然後計算過程同第一種方式，即$$mathcal{Z}_{t}=left[begin{array}{cccc}h(hat{mathcal{X}}_{t}^{*[1]}) & h(hat{mathcal{X}}_{t}^{*[2]}) & cdots & h(hat{mathcal{X}}_{t}^{*[2m+1]}) end{array}right]$$

最後估計觀測的均值和協方差矩陣，進而得到最終的結果，Unscented Kalman Filter的求解過程可歸納為：

初始化$mu_0$以及$Sigma_0$
預測：$hat{mu}_t=sum_{j=1}^{2m+1}w_{aj}hat{mathcal{X}}_{t}^{[j]}$以及$hat{Sigma}_t=sum_{j=1}^{2m+1}w_{cj}(hat{mathcal{X}}_{t}^{[j]}-hat{mu}_t)(hat{mathcal{X}}_{t}^{[j]}-hat{mu}_t)^T+Q$
計算$mathcal{Z}_{t}$（從上述兩種方式中選擇一種），得到$mu_{O_t}=sum_{j=1}^{2m+1}w_{aj}mathcal{Z}_{t}^{[j]}$以及$Sigma_{OO}=sum_{j=1}^{2m+1}w_{cj}({mathcal{Z}}_{t}^{[j]}-mu_{O_t})({mathcal{Z}}_{t}^{[j]}-mu_{O_t})^T+V$
計算$Sigma_{PO}=sum_{j=1}^{2m+1}w_{cj}(hat{mathcal{X}}_{t}^{[j]}-hat{mu}_{t})({mathcal{Z}}_{t}^{[j]}-mu_{O_t})^T$，注意若使用第二種方式計算$mathcal{Z}_t$，需將公式中的$hat{mathcal{X}}_{t}$替換為$hat{mathcal{X}}_{t}^*$
計算卡爾曼增益矩陣$K_t=Sigma_{PO}Sigma_{OO}^{-1}$
更新：$mu_t=hat{mu}_t+K_t[x_t-mu_{O_t}]$以及$Sigma_t=hat{Sigma}_t-Sigma_{PO}Sigma_{OO}^{-1}Sigma_{PO}^T=hat{Sigma}_t-K_tSigma_{OO}K_t^T$